�n�~���g���E�P�[���[�̒藝�@�@�@�֘A���
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���̍��ڂ́A�ŗL�l�E�ŗL�x�N�g�����Q�Ƃ��Ă��������B
�n�~���g���E�P�[���[�̒藝�Fn�������s��A�̌ŗL�������F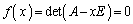 ��x��A�ɕς����s��̑������ɂ��āA
��x��A�ɕς����s��̑������ɂ��āA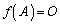 (��s��)
(��s��)
2���̐����s��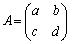 �ɂ��ẮA
�ɂ��ẮA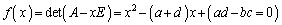 ��x��A�ɕς����s��̑������ɂ��āA
��x��A�ɕς����s��̑������ɂ��āA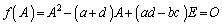 (��s��)
(��s��)
[�ؖ�]�@��w�����ł́A2���̐����s��Ɋւ�����̂����o�肳��Ȃ��̂ŁA�ȉ����L������Ă���n�j�ł��B
2���̐����s��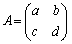 �ɂ��āA
�ɂ��āA
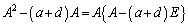
�@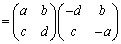
�@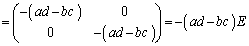
�� 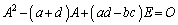
n�������s��A�ɂ��āAA�̌ŗL�lk�́A�ŗL�������F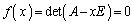 �̉��ł��B
�̉��ł��B
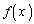 ��W�J���āA
��W�J���āA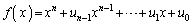 �Ə������Ƃ��܂��B
�Ə������Ƃ��܂��B
�ŗL�lk�ɂ��āA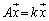 �ƂȂ�x�N�g��(�ŗL�x�N�g��)�����݂��A
�ƂȂ�x�N�g��(�ŗL�x�N�g��)�����݂��A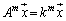 (
(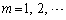 )�ł��B
)�ł��B
�s��A���قȂ�ŗL�l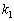 �C
�C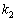 �C����C
�C����C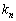 (
(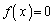 �̉�)�����Ƃ��A�����̌ŗL�l�ɑ���ŗL�x�N�g��
�̉�)�����Ƃ��A�����̌ŗL�l�ɑ���ŗL�x�N�g��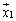 �C
�C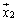 �C����C
�C����C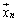 ��1���Ɨ��ŁAn�����x�N�g����ԓ��̔C�ӂ̃x�N�g��
��1���Ɨ��ŁAn�����x�N�g����ԓ��̔C�ӂ̃x�N�g��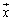 �́A
�́A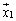 �C
�C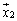 �C����C
�C����C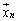 ��1�������̌`�ɕ\�����Ƃ��ł��܂��B
��1�������̌`�ɕ\�����Ƃ��ł��܂��B
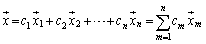
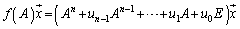
�@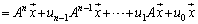
�@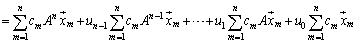
�@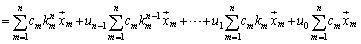
�@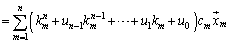
�@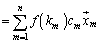
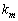 �͌ŗL������
�͌ŗL������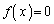 �̉��Ȃ̂ŁA
�̉��Ȃ̂ŁA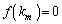 �ł��B�܂�A
�ł��B�܂�A
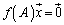 �@����@
�@����@
���ꂪ�An������ԓ��̔C�ӂ̃x�N�g��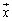 �ɂ��Đ��藧�̂ŁA
�ɂ��Đ��藧�̂ŁA
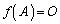
(�ؖ��I)
��1�D��L�@�̕��������������ڂ��������ƁA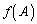 �Ƃ����s���C�ӂ̃x�N�g��
�Ƃ����s���C�ӂ̃x�N�g��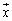 �ɂ�����
�ɂ�����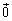 �ɂȂ�̂Ȃ�A
�ɂȂ�̂Ȃ�A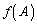 �͗�s��ɂȂ�ƌ����Ă��܂��B�܂�A
�͗�s��ɂȂ�ƌ����Ă��܂��B�܂�A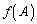 ��
��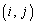 ������
������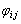 �C
�C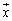 �̑����s������
�̑����s������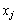 �Ƃ��āA�@�́A
�Ƃ��āA�@�́A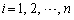 �ɑ��āA
�ɑ��āA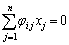 �@����A�@�����藧�Ƃ������Ƃł��B�C�ӂ�
�@����A�@�����藧�Ƃ������Ƃł��B�C�ӂ�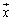 �ɂ��Đ��藧�̂ŁA�A��
�ɂ��Đ��藧�̂ŁA�A��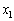 �C
�C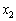 �C����C
�C����C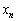 ���C�ӂ̎����ł��B�C�ӂ̎���
���C�ӂ̎����ł��B�C�ӂ̎���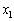 �C
�C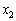 �C����C
�C����C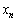 �ɑ��ćA���P���I�ɐ�����������́A
�ɑ��ćA���P���I�ɐ�����������́A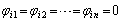 (
(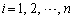 )�ł��B�����A
)�ł��B�����A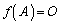 �Ƃ������ƂɂȂ�܂��B
�Ƃ������ƂɂȂ�܂��B
��2�D��L�ł́A�s��A���قȂ�n�̌ŗL�l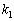 �C
�C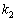 �C����C
�C����C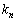 �����A�܂�A�ŗL������
�����A�܂�A�ŗL������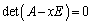 ���قȂ�n�̉������ꍇ�݂̂ŏ����Ă���܂����A�ŗL��������l�d��
���قȂ�n�̉������ꍇ�݂̂ŏ����Ă���܂����A�ŗL��������l�d��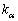 �����ꍇ(�ul�d�ɏk�ނ��Ă���v�ƌ����܂�)�ł��A�ŗL�l
�����ꍇ(�ul�d�ɏk�ނ��Ă���v�ƌ����܂�)�ł��A�ŗL�l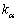 �ɑ���l��1���Ɨ��ȌŗL�x�N�g�����Ƃ邱�Ƃ��ł���ꍇ�ɂ́A
�ɑ���l��1���Ɨ��ȌŗL�x�N�g�����Ƃ邱�Ƃ��ł���ꍇ�ɂ́A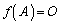 ���������Ƃ��ł��܂��B
���������Ƃ��ł��܂��B
����Ɍ����ƁAl�d��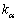 �ɑΉ�����1���Ɨ��ȌŗL�x�N�g����l�����������݂��Ȃ��ꍇ������̂ł����A
�ɑΉ�����1���Ɨ��ȌŗL�x�N�g����l�����������݂��Ȃ��ꍇ������̂ł����A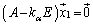 �����ŗL�x�N�g��
�����ŗL�x�N�g��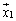 �ɑ��āA
�ɑ��āA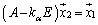 �ƂȂ�x�N�g��
�ƂȂ�x�N�g��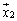 �������Ă���A
�������Ă���A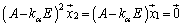 �̂悤�ɂł���̂ŁA
�̂悤�ɂł���̂ŁA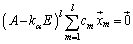 �ƂȂ�悤�ɁA1���Ɨ���l�̃x�N�g���̑g
�ƂȂ�悤�ɁA1���Ɨ���l�̃x�N�g���̑g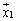 �C
�C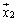 �C����C
�C����C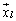 ���Ƃ邱�Ƃ��ł��āA
���Ƃ邱�Ƃ��ł��āA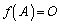 ���������Ƃ��ł��܂��B
���������Ƃ��ł��܂��B
�s��A��1�����F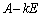 �̌`�ɂ��āA
�̌`�ɂ��āA
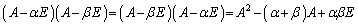
���A�����܂�(�W�J���Ă݂�n�j)�B�s��̐ς͈�ʂɂ͍��E�����ւ���ƈقȂ�s��ɂȂ��Ă��܂��܂�(�s��̐����Q��)���A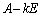 �Ƃ����`�̍s��̐ςł͍��E�����ւ��Ă���������(������A�����\�A�Ƃ��A���ƌ����܂�)�ƂȂ�܂��B
�Ƃ����`�̍s��̐ςł͍��E�����ւ��Ă���������(������A�����\�A�Ƃ��A���ƌ����܂�)�ƂȂ�܂��B
�]���āA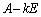 �Ƃ����`�ōs��̐ς������͈͂ɂ����ẮA�s��A�Ɋւ���a�E���E�ς̌v�Z�𐔂̌v�Z�Ɠ��l�ɍs�����Ƃ��ł��܂��B
�Ƃ����`�ōs��̐ς������͈͂ɂ����ẮA�s��A�Ɋւ���a�E���E�ς̌v�Z�𐔂̌v�Z�Ɠ��l�ɍs�����Ƃ��ł��܂��B
���A�ŗL���������A
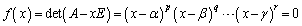 �@����B
�@����B
�̂悤�Ɉ�����������Ă����Ƃ��܂��B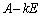 �Ƃ����`�ōs��̐ς������͈͂ɂ����ẮA���Ɠ����悤�Ɍv�Z�ł���̂ŁA�ŗL��������x���s��A�ɒu�����������������悤�Ɉ������������`�Ő������܂��B
�Ƃ����`�ōs��̐ς������͈͂ɂ����ẮA���Ɠ����悤�Ɍv�Z�ł���̂ŁA�ŗL��������x���s��A�ɒu�����������������悤�Ɉ������������`�Ő������܂��B
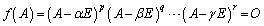 �@����C
�@����C
�܂�A�n�~���g���E�P�[���[�̒藝�ɂ���ď����ꂽ�s��̑������Ɋւ��铙���ł́A�������Ɠ������o�ň�������(���̕����ł͂���܂���)���ėǂ��A�Ƃ������ƂɂȂ�܂��B
�A���A���ӂ��ׂ����Ƃ�����܂��B�B���A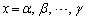 �͌����܂����A�C���A
�͌����܂����A�C���A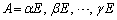 �Ƃ��邱�Ƃ͂ł��܂���B
�Ƃ��邱�Ƃ͂ł��܂���B
�Ⴆ�A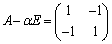 �C
�C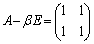 �Ƃ���ƁA
�Ƃ���ƁA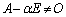 �C
�C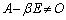 �ł����A
�ł����A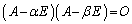 �ƂȂ�܂��B
�ƂȂ�܂��B
�n�~���g���E�P�[���[�̒藝�́A�ȉ��̗�̂悤�ɁA�s��̑������̎����������邱�Ƃɗ��p����܂��B
��1�D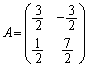 �̂Ƃ��A
�̂Ƃ��A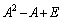 �����߂�B
�����߂�B
[��]�@�s��̐��������̂܂g����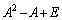 ���v�Z����̂ł͑������܂��B
���v�Z����̂ł͑������܂��B
�n�~���g���E�P�[���[�̒藝���A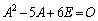
�� 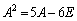
�� 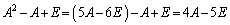
�@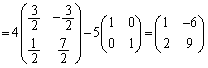 ......[��]
......[��]
��2�D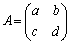 �̂Ƃ��A
�̂Ƃ��A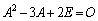 �@����@�@�����藧�B
�@����@�@�����藧�B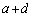 (
(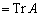 )�C
)�C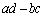 (
(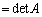 )�̒l�����߂�B
)�̒l�����߂�B
[��]�@�n�~���g���E�P�[���[�̒藝���A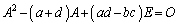 �@����A
�@����A
�@�C�A���W����r���āA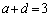 �C
�C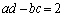 �Ƃ���Ă��܂��ƁA�s�\�����ɂȂ��Ă��܂��܂��B
�Ƃ���Ă��܂��ƁA�s�\�����ɂȂ��Ă��܂��܂��B
��1�D�Ɠ����悤�ɁA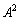 ����������A�Ƃ������j�ŗՂ݂܂��B
����������A�Ƃ������j�ŗՂ݂܂��B
�A���A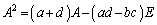
�@�ɑ�����āA
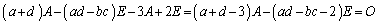 �@����B
�@����B
�����ŁA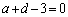 �ł���A
�ł���A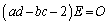
�� 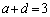 �C
�C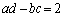
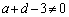 �ł���A�B����
�ł���A�B����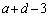 �Ŋ����āA
�Ŋ����āA
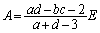
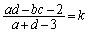 �Ƃ����ƁA
�Ƃ����ƁA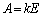
������@�ɑ������ƁA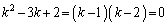
�� 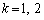
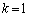 �̂Ƃ��A
�̂Ƃ��A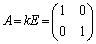
�� 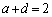 �C
�C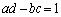
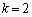 �̂Ƃ��A
�̂Ƃ��A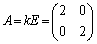
�� 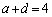 �C
�C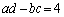
�ȏ���A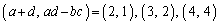 ......[��]
......[��]
��3�D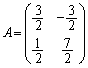 �̂Ƃ��A
�̂Ƃ��A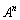 (
(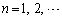 )�����߂�B
)�����߂�B
[��]�@�n�~���g���E�P�[���[�̒藝���A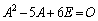
�s��Ŋ���Z���ł���A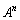 ��
��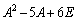 �Ŋ���悢�̂ł����A�c�O�Ȃ��琔�Ɠ����悤�Ȋ��o�Ŋ���Z�����s���邱�Ƃ͂ł��܂���B
�Ŋ���悢�̂ł����A�c�O�Ȃ��琔�Ɠ����悤�Ȋ��o�Ŋ���Z�����s���邱�Ƃ͂ł��܂���B
�����ŁA�s��A��x�ɒu�������Ăł��鑽�����Ŋ���Z���s���܂��B
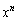 ��
��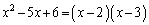 �Ŋ������]���
�Ŋ������]���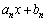 �C����
�C����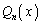 �Ƃ��āA
�Ƃ��āA
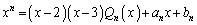 �@����@�@(�������̏��Z���Q��)
�@����@�@(�������̏��Z���Q��)
�@�ŁA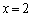 �Ƃ���ƁA
�Ƃ���ƁA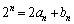 �@����A
�@����A
�@�ŁA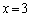 �Ƃ���ƁA
�Ƃ���ƁA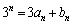 �@����B
�@����B
�B�|�A���A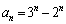
�A�~3�|�B�~2���A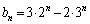
�@��x��A�ɖ߂��ƁA
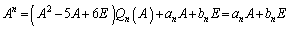
�@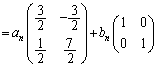
�@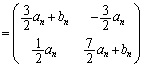
�@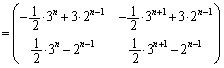 ......[��]
......[��]
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���w��b����TOP�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B 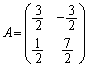 �̂Ƃ��A
�̂Ƃ��A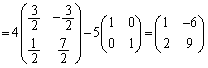 ......[��]
......[��]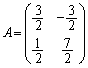 �̂Ƃ��A
�̂Ƃ��A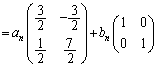
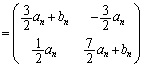
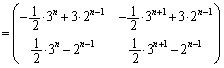 ......[��]
......[��]