�����㐔�w'10�N[2]
�\�̏o��m����p�C���̏o��m����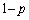 �̃R�C��������B���̃R�C���𓊂��A���̌��ʂɂ��A�2�_A�CB�̊Ԃ��ړ����A�|�C���g���l�����邱�Ƃ��J��Ԃ����̂悤�ȃQ�[�����s���B
�̃R�C��������B���̃R�C���𓊂��A���̌��ʂɂ��A�2�_A�CB�̊Ԃ��ړ����A�|�C���g���l�����邱�Ƃ��J��Ԃ����̂悤�ȃQ�[�����s���B
���[��a)�@��̓Q�[�����n�߂�Ƃ��_A�ɂ���
���[��b)�@��̓R�C�������ŕ\���o����̂Ƃ�����_�ɂƂǂ܂�A�����o���������̓_�Ɉړ�����
���[��c)�@k��ڂ̃R�C�������̌��ʁA��_A�ɂ���Ƃ���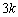 �|�C���g�V���Ɋl�����A�_B�ɂ���Ƃ���k�|�C���g�V���Ɋl������@(
�|�C���g�V���Ɋl�����A�_B�ɂ���Ƃ���k�|�C���g�V���Ɋl������@(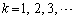 )
) n�����R���Ƃ��āA�ȉ��̖₢�ɓ�����B
(1) n��R�C���𓊂������ʁA��_A�ɂ���m����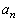 �Ƃ����B
�Ƃ����B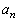 �����߂�B
�����߂�B (2) k��ڂ̃R�C�������̌��ʂɂ��V���Ɋl������|�C���g�̊��Ғl��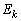 �Ƃ����B
�Ƃ����B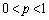 �̂Ƃ��A
�̂Ƃ��A ��n��p��p���ĕ\���B
��n��p��p���ĕ\���B (3) (1)�ŋ��߂�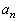 ��p�̊��ƍl���A
��p�̊��ƍl���A �Ə����Ƃ��A���̋Ɍ��l�����߂�B
�Ə����Ƃ��A���̋Ɍ��l�����߂�B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@�m���ƑQ�����̗Z�����ɁA�敪���ϖ@�̏����������Ă�����ł��B
(1) ���[��a)���A����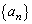 �̏���
�̏���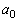 �ɂ��āA
�ɂ��āA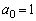 �ƍl���邱�Ƃɂ��܂��B
�ƍl���邱�Ƃɂ��܂��B 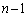 ��R�C���𓊂������ʋ�_A�ɂ���m����
��R�C���𓊂������ʋ�_A�ɂ���m����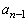 �ŁA�_B�ɂ���m����
�ŁA�_B�ɂ���m����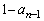 �ł��B
�ł��B
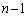 ��R�C���𓊂������ƁA�_A�ɂ�����n��ڂ̃R�C�������ŁA�m��p�ŕ\���o�ē_A�ɗ��܂�܂��B
��R�C���𓊂������ƁA�_A�ɂ�����n��ڂ̃R�C�������ŁA�m��p�ŕ\���o�ē_A�ɗ��܂�܂��B
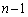 ��R�C���𓊂������ƁA�_B�ɂ�����n��ڂ̃R�C�������ŁA�m��
��R�C���𓊂������ƁA�_B�ɂ�����n��ڂ̃R�C�������ŁA�m��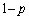 �ŗ����o�ē_A�Ɉڂ�܂��Bn��R�C���𓊂������ʁA��_A�ɂ���̂́A���2�̏ꍇ�ł����āA�����m��
�ŗ����o�ē_A�Ɉڂ�܂��Bn��R�C���𓊂������ʁA��_A�ɂ���̂́A���2�̏ꍇ�ł����āA�����m�� �́A
�́A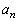 ��
�� ��α�Ƃ����āA
��α�Ƃ����āA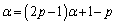 �@����A
�@����Aα�ɂ��ĉ����ƁA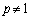 �ł���A
�ł���A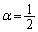
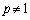 �̂Ƃ��A�@�|�A���A
�̂Ƃ��A�@�|�A���A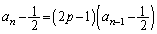
������A����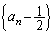 �́A����
�́A���� �C����
�C���� �����䐔���ł��B
�����䐔���ł��B �� 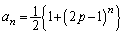 �@����B
�@����B
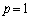 �̂Ƃ��A�@�́A
�̂Ƃ��A�@�́A �ƂȂ�܂����A�R�C�������ŕK���\���o��̂ŁA��͓_A�ɂ��Â��邱�ƂɂȂ�A
�ƂȂ�܂����A�R�C�������ŕK���\���o��̂ŁA��͓_A�ɂ��Â��邱�ƂɂȂ�A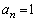 �ł��B����́A�B�Ɋ܂܂�܂��B
�ł��B����́A�B�Ɋ܂܂�܂��B 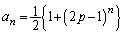 ......[��]
......[��]
(2) k��ڂ̃R�C�������̌��ʁA�A�ɂ���m���� �ŁA���̂Ƃ��̓��_��
�ŁA���̂Ƃ��̓��_��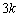 �C�B�ɂ���m����
�C�B�ɂ���m����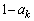 �ŁA���̂Ƃ��̓��_��k�ł��B(1)�̌��ʂ�p���āA���_�����Ғl
�ŁA���̂Ƃ��̓��_��k�ł��B(1)�̌��ʂ�p���āA���_�����Ғl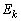 �́A
�́A 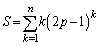 �Ƃ����ƁA
�Ƃ����ƁA �@����E
�@����E
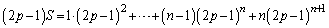 �@����F
�@����F�E�|�F���A
�� 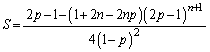 �@����G
�@����G
�C�C�D�C�G���A 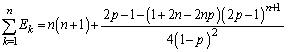 ......[��]
......[��]
(3) 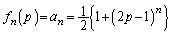
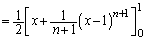
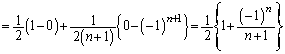 ......[��]
......[��]
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B 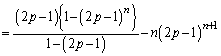
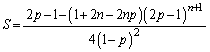 �@����G
�@����G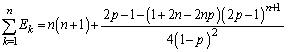 ......[��]
......[��]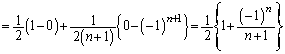 ......[��]
......[��]