北大数学'10年後期[3]
1辺の長さがaの正三角形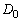 から出発して、多角形
から出発して、多角形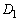 ,
,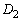 ,・・・,
,・・・,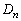 ,・・・・・・ を次のように定める。
,・・・・・・ を次のように定める。
(i) ABを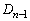 の1辺とする。辺ABを3等分し、その分点をAに近い方からP,Qとする。
の1辺とする。辺ABを3等分し、その分点をAに近い方からP,Qとする。 (ii) PQを1辺とする正三角形PQRを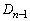 の外側に作る。
の外側に作る。 (iii) 辺ABを折れ線APRQBで置き換える。
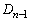 のすべての辺に対して(i)〜(iii)の操作を行って得られる多角形を
のすべての辺に対して(i)〜(iii)の操作を行って得られる多角形を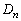 とする。
とする。
以下の問いに答えよ。
(1) 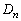 の周の長さ
の周の長さ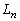 をaとnで表せ。
をaとnで表せ。 (2) 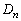 の面積
の面積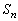 をaとnで表せ。
をaとnで表せ。 (3) 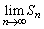 を求めよ。
を求めよ。
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
解答 フラクタルをテーマにした問題です。本問の操作によって得られる曲線をコッホ曲線と言います。図形の1部分をどんどん拡大していくと、普通は、だんだん滑らかな図形が現れてくるのですが、コッホ曲線のように、フラクタルでは拡大するとどんどん複雑な図形が現れてくるようになります。海岸線や雪の結晶など、自然界の現象では、フラクタルのような図形が現れることが知られています。
(1) 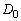 の周囲の長さは、長さaの1辺が3辺あるので、
の周囲の長さは、長さaの1辺が3辺あるので、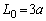 です。
です。 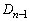 から
から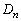 を作るとき、1辺の長さは、操作(i)で3等分されます。よって、
を作るとき、1辺の長さは、操作(i)で3等分されます。よって、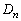 の1辺の長さは、
の1辺の長さは、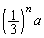 です(等比数列を参照)。
です(等比数列を参照)。
また、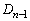 から
から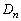 を作るとき、辺の個数は、1辺ABから、AP,PR,RQ,QBの4個の辺ができます。よって、
を作るとき、辺の個数は、1辺ABから、AP,PR,RQ,QBの4個の辺ができます。よって、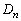 の辺の個数は、
の辺の個数は、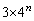 個です。
個です。
よって、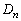 の周の長さは、
の周の長さは、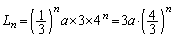 ......[答]
......[答]
(2) 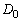 の面積は、
の面積は、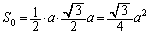
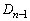 から
から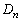 を作るとき、
を作るとき、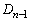 の各辺について、1つの辺に接するように正三角形1個が付け加わり、正三角形の個数分の面積が増大します。正三角形の個数は
の各辺について、1つの辺に接するように正三角形1個が付け加わり、正三角形の個数分の面積が増大します。正三角形の個数は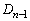 の辺の個数に一致し、
の辺の個数に一致し、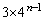 個です。
個です。
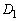 を作るときに付け加わる正三角形1個の面積は、
を作るときに付け加わる正三角形1個の面積は、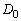 の面積の
の面積の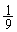 で、
で、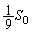 です。
です。
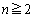 のとき、
のとき、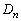 を作るときに付け加わる正三角形1個の面積は、
を作るときに付け加わる正三角形1個の面積は、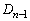 を作るときに付け加わる正三角形1個の面積の
を作るときに付け加わる正三角形1個の面積の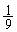 で(辺の長さは
で(辺の長さは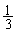 )、
)、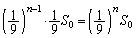 です。
です。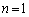 のときもこうなります。
のときもこうなります。
よって、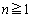 のとき、
のとき、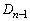 から
から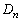 を作るときに増大する面積は、
を作るときに増大する面積は、
∴ 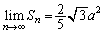 ......[答]
......[答] 追記.(3)の結果と、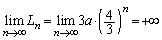 より、操作を無限に繰り返していくと、
より、操作を無限に繰り返していくと、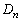 は、有限な面積
は、有限な面積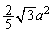 をもつのに、無限に周の長い図形になっていくことがわかります。
をもつのに、無限に周の長い図形になっていくことがわかります。
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
数学TOP TOPページに戻る
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
各問題の著作権は
出題大学に属します。©2005-2024(有)りるらる 苦学楽学塾 随時入会受付中!理系大学受験ネット塾苦学楽学塾(ご案内はこちら)ご入会は、
まず、こちらまでメールを
お送りください。