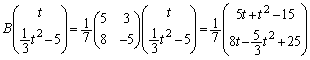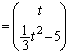�k�吔�w'10�N���[4]
���W���ʏ�̓_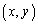 ��_
��_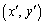 �Ɉڂ��_�̈ړ�f ���s��
�Ɉڂ��_�̈ړ�f ���s�� ��p����
��p����
�ŕ\�����Ƃ��Af ��1���ϊ��Ƃ����B���̂Ƃ�A��1���ϊ�f ��\���s��Ƃ����B
t�������Ƃ��A���W���ʏ��3�_P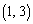 �CQ
�CQ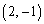 �CR
�CR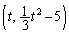 ���Ƃ�B
���Ƃ�B
(1) P��Q�Ɉڂ��AQ��P�Ɉڂ�1���ϊ�g��\���s������߂�B
(2) ����ɁAg��R��R���g�Ɉڂ��Ƃ���B���̂Ƃ���t ��R�����߂�B
(3) ��ŋ��߂�R�̂���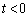 �ł�����̂ɂ��āA�W��
�ł�����̂ɂ��āA�W��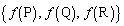 ���W��
���W��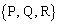 �Ɠ������Ȃ�悤��1���ϊ�f �̌������߂�B�������AP�CQ�CR��f �ňڂ����_�����ꂼ��
�Ɠ������Ȃ�悤��1���ϊ�f �̌������߂�B�������AP�CQ�CR��f �ňڂ����_�����ꂼ��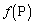 �C
�C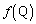 �C
�C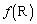 �Ƃ���B
�Ƃ���B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@1���ϊ��Ɋւ�����ł����A�{��ł́A�s��Ɋւ���ȉ��̋Z�I���g���܂��B
2��1���Ɨ��ȃx�N�g��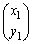 �C
�C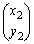 �ɂ��āA
�ɂ��āA
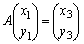 �C
�C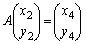 �@����@
�@����@
���A�@��2����1�ɂ܂Ƃ߂āA
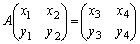 �@���(��)
�@���(��)
(1) 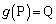 �C
�C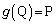 ���Ag��\���s���B�Ƃ��āA
���Ag��\���s���B�Ƃ��āA 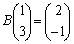 �C
�C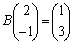
(��)��p���āA
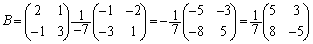 ......[��]
......[��]
(2) 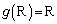 ���A
���A �� 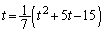 �C
�C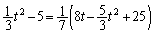
�����Ƃ��ό`����ƁA����̕������A �ƂȂ�A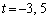 ......[��]
......[��]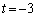 �̂Ƃ��AR
�̂Ƃ��AR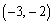 �C
�C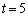 �̂Ƃ��AR
�̂Ƃ��AR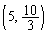 ......[��]
......[��]
(3)(i) (1)�C(2)��1���ϊ�g�́A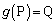 �C
�C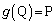 �C
�C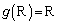 ���A
���A 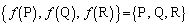 �@����@
�@����@�����܂��B
(ii) �P���ϊ�e (�C�ӂ̃x�N�g��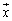 �ɂ���
�ɂ���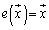 )��\���s��́A�P�ʍs��
)��\���s��́A�P�ʍs��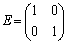 �ł����A
�ł����A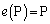 �C
�C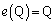 �C
�C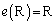 �ƂȂ�̂ŁA�@�����܂��B
�ƂȂ�̂ŁA�@�����܂��B �@�ƂȂ�\����(i)�C(ii)�ȊO�ɁA
��4�ʂ肵������܂���B
(iii)�����藧�Ƃ���ƁA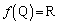 �C
�C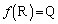 ���A
���A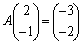 �C
�C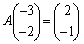
�� 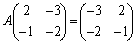
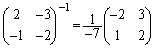 ���E���炩���āA
���E���炩���āA ���̂Ƃ��A
���A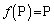 �ƂȂ�A�@�����܂��B
�ƂȂ�A�@�����܂��B (iv)�����藧�Ƃ���ƁA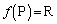 �C
�C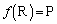 ���A
���A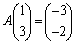 �C
�C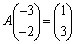
�� 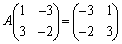
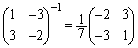 ���E���炩���āA
���E���炩���āA ���̂Ƃ��A
���A �ƂȂ�A�@�����܂��B
�ƂȂ�A�@�����܂��B (v)�����藧�Ƃ���ƁA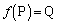 �C
�C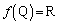 ���A
���A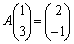 �C
�C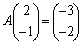
�� 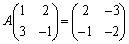
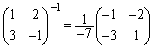 ���E���炩���āA
���E���炩���āA ���̂Ƃ��A
���A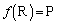 �ƂȂ�A�@�����܂��B
�ƂȂ�A�@�����܂��B (vi)�����藧�Ƃ���ƁA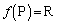 �C
�C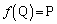 ���A
���A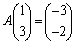 �C
�C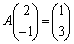
�� 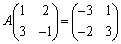
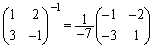 ���E���炩���āA
���E���炩���āA ���̂Ƃ��A
���A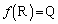 �ƂȂ�A�@�����܂��B
�ƂȂ�A�@�����܂��B
�ȏ���A�@����1���ϊ���(i)�`(vi)�́A6�� ......[��]
�NjL�D�{��ł́A�s���3�_�̍��W����̓I�Ɏw�肳��Ă��܂����A�w��Ȃ��ōl���Ă݂܂��B�O�p�`ABC��3���_A�CB�CC�̈ʒu�x�N�g����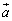 �C
�C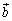 �C
�C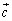 �Ƃ��A
�Ƃ��A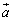 �C
�C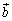 ��1���Ɨ����Ƃ��܂��Bs�Ct�������Ƃ��āA
��1���Ɨ����Ƃ��܂��Bs�Ct�������Ƃ��āA �Ƃ������Ƃ��ł��܂��B
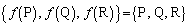 �@����@
�@����@�����\���́A��L�ŏ������悤�Ɉȉ���6�ʂ肵������܂���B
(ii)�͍P���ϊ��Ň@�͖�������܂��B
(i)�����藧���Af ��\���s���݂���Ƃ��āA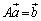 �C
�C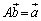
�� 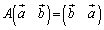
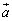 �C
�C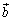 ��1���Ɨ��Ȃ̂�
��1���Ɨ��Ȃ̂�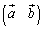 �͐���(�t�s����)�ŁA�E����
�͐���(�t�s����)�ŁA�E����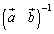 �������āA
�������āA �Ƃ���A����܂�܂��B
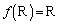 �ƂȂ邽�߂ɁA
�ƂȂ邽�߂ɁA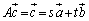
������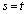 �ł���A�@�͖�������܂��B
�ł���A�@�͖�������܂��B �ȉ����l��(iii)�`(iv)�ɂ����Ă�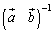 �����݂���1���ϊ�f��\���s��܂�܂��B
�����݂���1���ϊ�f��\���s��܂�܂��B (iii)�����藧�Ƃ���ƁA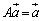 �C
�C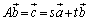
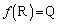 �ƂȂ邽�߂ɁA
�ƂȂ邽�߂ɁA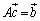
������A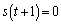 ����
���� 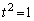 �C�]���āA
�C�]���āA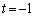 �܂��� �e
�܂��� �e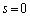 ����
����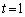 '�ƂȂ�܂����A�e
'�ƂȂ�܂����A�e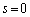 ����
����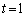 '�̂Ƃ��ɂ�
'�̂Ƃ��ɂ�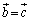 �ƂȂ�O�p�`���ł��܂���B
�ƂȂ�O�p�`���ł��܂���B
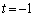 �ł���A�@����������܂��B
�ł���A�@����������܂��B (iv)�����藧�Ƃ���ƁA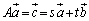 �C
�C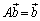
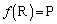 �ƂȂ邽�߂ɁA
�ƂȂ邽�߂ɁA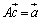
������A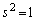 ����
���� 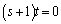 �C�]���āA
�C�]���āA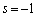 �܂��� �e
�܂��� �e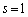 ����
����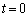 '�ƂȂ�܂����A�e
'�ƂȂ�܂����A�e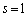 ����
����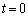 '�̂Ƃ��ɂ�
'�̂Ƃ��ɂ�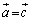 �ƂȂ�O�p�`���ł��܂���B
�ƂȂ�O�p�`���ł��܂���B
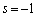 �ł���A�@����������܂��B
�ł���A�@����������܂��B (v)�����藧�Ƃ���ƁA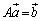 �C
�C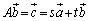
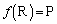 �ƂȂ邽�߂ɁA
�ƂȂ邽�߂ɁA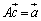
������A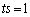 ����
���� 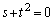 �C�]���āA
�C�]���āA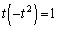 �C
�C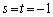 �ł���A�@�͖�������܂��B
�ł���A�@�͖�������܂��B (vi)�����藧�Ƃ���ƁA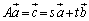 �C
�C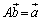
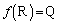 �ƂȂ邽�߂ɁA
�ƂȂ邽�߂ɁA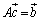
������A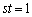 ����
���� 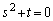 �C�]���āA
�C�]���āA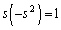 �C
�C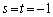 �ł���A�@�͖�������܂��B
�ł���A�@�͖�������܂��B �]���āA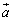 �C
�C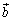 ��1���Ɨ��ł����f ��\���s���݂��A
��1���Ɨ��ł����f ��\���s���݂��A
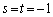 �ł���A(i)�`(vi)��6��1���ϊ����@�����܂��B
�ł���A(i)�`(vi)��6��1���ϊ����@�����܂��B
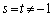 �ł���A(i)�C(ii)��2��1���ϊ����@�����܂��B
�ł���A(i)�C(ii)��2��1���ϊ����@�����܂��B
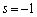 �C
�C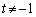 �܂���
�܂��� 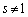 �C
�C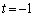 �ł���A(i)�C(ii)�C(iv)�C(v)��4��1���ϊ����@�����܂��B
�ł���A(i)�C(ii)�C(iv)�C(v)��4��1���ϊ����@�����܂��B
�{��ł́A �Ƃ���ƁA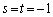 �ƂȂ�̂ŁA�@����1���ϊ���6����A�Ƃ������ƂɂȂ�܂��B
�ƂȂ�̂ŁA�@����1���ϊ���6����A�Ƃ������ƂɂȂ�܂��B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B