広島大理系数学'10年後期[1]
自然数のうち、2と8がどの桁にも現れないものを考え、それらを小さい方から重に並べた数列
1, 3, 4, 5, 6, 7, 9, 10, 11, 13, 14, 15, 16, 17, 19, 30, 31, 33, ･･･
を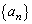
とする。いま、自然数mに対し、数列
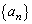の中にあるm桁の整数の個数を
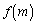とする。例えば
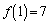である。このとき、以下の問いに答えよ。
(1) 
，
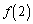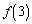を求めよ。 (2) 自然数mに対し、
を求めよ。 (3) 自然数mに対し、数列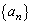
の中にあるm桁の整数の逆数の総和は
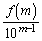より小さいことを示せ。 (4) すべての自然数nに対し、
が成り立つことを示せ。
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
解答 難問に見えますが、親切な誘導に沿って進めば標準問題です。試験会場でパスしないようにしましょう。
(1) 2桁の自然数で、10の位にも、1の位にも、2と8が現れない数は、
10の位が、1, 3, 4, 5, 6, 7, 9の7通り、1の位が、0, 1, 3, 4, 5, 6, 7, 9の8通り、
よって、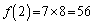
......[答] (場合の数を参照)
3桁の自然数で、100の位にも、10の位にも、1の位にも、2と8が現れない数は、100の位が、1, 3, 4, 5, 6, 7, 9の7通り、10の位が、0, 1, 3, 4, 5, 6, 7, 9の8通り、1の位が、0, 1, 3, 4, 5, 6, 7, 9の8通り、
よって、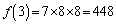
......[答]
(2) 
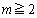のとき、m桁の自然数で、各桁に2と8が現れない数は、 
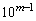の位が、1, 3, 4, 5, 6, 7, 9の7通り、
の位から
の位まで、0, 1, 3, 4, 5, 6, 7, 9の8通り、
よって、
(
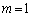のときも成り立ちます)自然数mに対し、
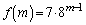......[答] (等比数列を参照)
(3) 自然数mに対し、数列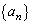
の中にあるm桁の整数が、第k項から第l項まで(項数は
)に位置しているとします。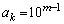 
，
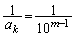
よって、自然数mに対し、数列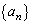
の中にあるm桁の整数の逆数の総和は
よりも小さくなります。
(4) (3)に出てくる数列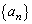
の中にあるm桁の整数の逆数の総和を
とします。(3)の結果より、 です。
がM桁の整数だとすると、(3)の結果を
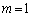から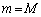
までで考えることにより、 (2)の結果を用いると、Mは有限な値なので、
無限等比級数
は、初項7，公比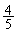
の無限等比級数ですが、公比の絶対値は1よりも小さいので、収束して和をもち、 以上より、
すべての自然数nに対し、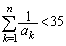
が成り立ちます。
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
数学TOP TOPページに戻る
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
各問題の著作権は
出題大学に属します。©2005-2024(有)りるらる 苦学楽学塾 随時入会受付中！理系大学受験ネット塾苦学楽学塾(ご案内はこちら)ご入会は、
まず、こちらまでメールを
お送りください。 
のとき、
，
なので、すべての自然数mに対し、
(
は、
の
項の和)
