�������吔�w'10�N[3]
���W���ʂɂ����āA�_C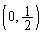 �𒆐S�Ƃ��A���a��
�𒆐S�Ƃ��A���a�� �̉~��S�Ƃ���BS��ɓ_N
�̉~��S�Ƃ���BS��ɓ_N ���Ƃ�A
���Ƃ�A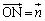 �Ƃ���B���̂Ƃ��A���̊e�₢�ɓ�����B�������AO�͌��_��\�����̂Ƃ���B
�Ƃ���B���̂Ƃ��A���̊e�₢�ɓ�����B�������AO�͌��_��\�����̂Ƃ���B
(1) x����ɓ_P ���Ƃ�A����NP�Ɖ~S�Ƃ̌�_�̂����AN�ƈقȂ���̂�Q�Ƃ���B
���Ƃ�A����NP�Ɖ~S�Ƃ̌�_�̂����AN�ƈقȂ���̂�Q�Ƃ���B �Ƃ����A
�Ƃ����A ��
��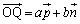 �̌`�ŕ\�����Ƃ��Aa�Cb��x�ŕ\���B
�̌`�ŕ\�����Ƃ��Aa�Cb��x�ŕ\���B (2) x�����2�_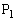
 �C
�C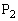
 ���Ƃ�B����
���Ƃ�B���� �Ɖ~S�Ƃ̌�_�̂����AN�ƈقȂ���̂�
�Ɖ~S�Ƃ̌�_�̂����AN�ƈقȂ���̂�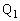 �Ƃ��A����
�Ƃ��A���� �Ɖ~S�Ƃ̌�_�̂����AN�ƈقȂ���̂�
�Ɖ~S�Ƃ̌�_�̂����AN�ƈقȂ���̂�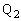 �Ƃ���B���̂Ƃ��A
�Ƃ���B���̂Ƃ��A �����藧���Ă����
�����藧���Ă���� ���������邱�Ƃ��ؖ�����B�������A �͗�x�N�g����\�����̂Ƃ���B
�͗�x�N�g����\�����̂Ƃ���B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@�����v�Z�𗘗p���镽�ʃx�N�g���̌v�Z���ł��B(1)���Ȃ���(2)�����ɂȂ��Ă�����ł��A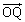 ��1�������̌`�ɕ\���悤�ɂ��܂��傤�B
��1�������̌`�ɕ\���悤�ɂ��܂��傤�B
�ƂȂ��Ă��܂��B
�ƕ\���Ƃ��AN�CQ�CP�͈꒼����̓_�Ȃ̂ŁA
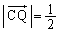 ���A
���A��  ��
�� 
 �̂Ƃ��A���
�̂Ƃ��A��� �ŁA
�ŁA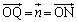 �ƂȂ��Ă��܂��̂ŕs�K�B
�ƂȂ��Ă��܂��̂ŕs�K�B  �̂Ƃ��A���
�̂Ƃ��A���
�� 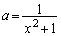 �C
�C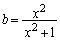 ......[��]������Ax�������̒P�ʃx�N�g��
......[��]������Ax�������̒P�ʃx�N�g��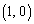 ��
��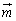 �Ƃ��āA
�Ƃ��āA ���A
���A  �@����B
�@����B
(2) �B�ɂ����āA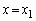 �Ƃ��邱�Ƃɂ��A
�Ƃ��邱�Ƃɂ��A �B�ɂ����āA �Ƃ��邱�Ƃɂ��A
�Ƃ��邱�Ƃɂ��A 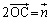 ���A
���A�����ŁA �C
�C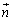 �̌W���ɂ��āA
�̌W���ɂ��āA ����āA
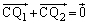 �@(�ؖ��I)
�@(�ؖ��I)
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B 
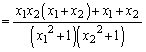
 �@(��
�@(�� 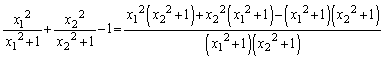

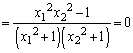 �@(��
�@(��