�É��吔�w'10�N[1]
k��萔�Ƃ���B2��������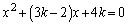 ��2�̎�����α�Cβ �������Aα�Cβ ��
��2�̎�����α�Cβ �������Aα�Cβ ��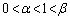 �������̂Ƃ���B���̂Ƃ��A���̖₢�ɓ�����B
�������̂Ƃ���B���̂Ƃ��A���̖₢�ɓ�����B
(1) k�̒l�͈̔͂����߂�B
(2) 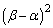 ��k��p���ĕ\���B
��k��p���ĕ\���B (3) α��β �̍��������ł���Ƃ���k�����α�Cβ �̒l�����߂�B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@2 �����E2���������Ɛ����̗Z�����ł��B
(1) 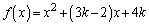 �Ƃ����ƁA2��������
�Ƃ����ƁA2��������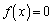 �����A2������α�Cβ �����̂ŁA
�����A2������α�Cβ �����̂ŁA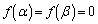 �ł��B
�ł��B 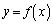 �̃O���t�͉��ɓʂȕ������ŁA
�̃O���t�͉��ɓʂȕ������ŁA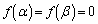 �Ƃ������Ƃ́A
�Ƃ������Ƃ́A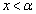 �ɂ�����
�ɂ�����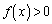 �C
�C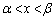 �ɂ�����
�ɂ�����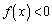 �C
�C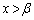 �ɂ�����
�ɂ�����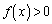 �ƂȂ�(2�������Q��)�Ƃ������Ƃł��B����āA2��������
�ƂȂ�(2�������Q��)�Ƃ������Ƃł��B����āA2��������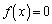 �̉�α�Cβ ��
�̉�α�Cβ ��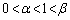 ��
�� 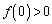 ����
���� 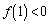 �@(2���������̉��̔z�u���Q��)
�@(2���������̉��̔z�u���Q��)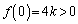 �@����@
�@����@
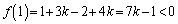 �@����A
�@����A�@���A���A
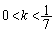 ......[��]
......[��]
(2) 2��������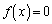 �̔��ʎ�D�F
�̔��ʎ�D�F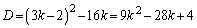
2��������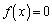 ��2���́A
��2���́A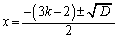
�� 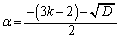 �C
�C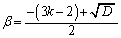 �@����@
�@����@
(3) p�𐮐��Ƃ��āA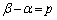 �Ƃ���ƁA(2)��p���āA
�Ƃ���ƁA(2)��p���āA �Ƃ��āA(1)���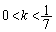 �ł����A
�ł����A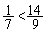 �Ȃ̂ŁA
�Ȃ̂ŁA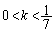 �ɂ�����
�ɂ�����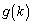 �͒P�������ł��B
�͒P�������ł��B 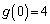 �C
�C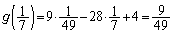
�� 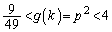 �������������
�������������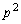 �́A
�́A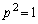 �݂̂ł��B���̂Ƃ��A
�݂̂ł��B���̂Ƃ��A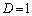 �ŁA
�ŁA 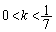 ���A
���A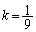 ......[��]�@���A
......[��]�@���A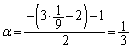 �C
�C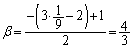 ......[��]
......[��]
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B