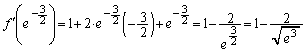�É��嗝���w'10�N[2]
���̖₢�ɓ�����B
(1) �s����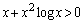 �����藧���Ƃ������B
�����藧���Ƃ������B (2) ��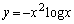 �̑����A�O���t�̉��ʂׁA�O���t�̊T�`�������B
�̑����A�O���t�̉��ʂׁA�O���t�̊T�`�������B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@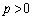 �Ƃ��āA
�Ƃ��āA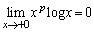 �����m�Ƃ��ĔF�߂Ă��܂��ΒP�Ȃ�v�Z���ł����A�ȉ��ł́A
�����m�Ƃ��ĔF�߂Ă��܂��ΒP�Ȃ�v�Z���ł����A�ȉ��ł́A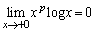 �����m�Ƃ��Ȃ��ł���Ă݂܂��B�f���ɍl���čs���ƓD�ꎮ�ɂȂ��Ă��܂����A���w�̕��A�Ƃ́A�����������̂����m��܂���B
�����m�Ƃ��Ȃ��ł���Ă݂܂��B�f���ɍl���čs���ƓD�ꎮ�ɂȂ��Ă��܂����A���w�̕��A�Ƃ́A�����������̂����m��܂���B
(1) 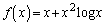
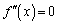 �Ƃ���ƁA
�Ƃ���ƁA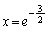
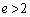 ���
���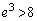 �C
�C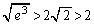 �C����āA
�C����āA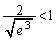
�� 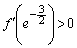
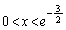 �ɂ�����
�ɂ�����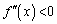 ��
��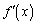 �͑����C
�͑����C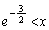 �ɂ�����
�ɂ�����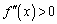 ��
��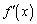 �͌���(���̑������Q��)�B
�͌���(���̑������Q��)�B
�ȏ���A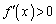 �C
�C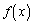 �͒P�������B
�͒P�������B
�����ŁA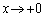 �Ƃ����Ƃ��ɁA
�Ƃ����Ƃ��ɁA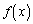 ��0�ȏ�̒l�ɋ߂Â��čs����
��0�ȏ�̒l�ɋ߂Â��čs����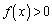 ��������@����@�@�̂ł����A���́A
��������@����@�@�̂ł����A���́A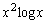 �ł��B
�ł��B
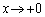 �̂Ƃ�
�̂Ƃ�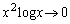 �����m�Ƃ��Ă��悢�����m��܂��A�����ł́A�m�F���Ă������Ƃɂ��܂��B
�����m�Ƃ��Ă��悢�����m��܂��A�����ł́A�m�F���Ă������Ƃɂ��܂��B
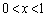 �ɂ�����
�ɂ�����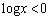 ��
��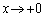 �̂Ƃ�
�̂Ƃ�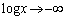 �Ȃ̂ŁA
�Ȃ̂ŁA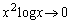 ���������߂ɂ́A
���������߂ɂ́A
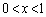 �ɂ�����
�ɂ�����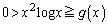 �ƂȂ�A
�ƂȂ�A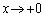 �̂Ƃ�
�̂Ƃ�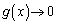 �ƂȂ��
�ƂȂ��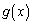 �������Ă��āA�͂��݂����ɂ��邱�ƂɂȂ�܂��B
�������Ă��āA�͂��݂����ɂ��邱�ƂɂȂ�܂��B
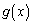 �̌��́A
�̌��́A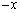 �ł��B
�ł��B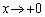 �̂Ƃ��A
�̂Ƃ��A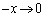 �ł��B
�ł��B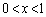 �ɂ����āA
�ɂ����āA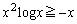 �ł����Ă����悢(���̕s�����ɖ߂��Ă��܂��܂�)�̂ł����Ax�ŗ��ӂ�����ƁA
�ł����Ă����悢(���̕s�����ɖ߂��Ă��܂��܂�)�̂ł����Ax�ŗ��ӂ�����ƁA �ɂȂ�̂ŁA
�ɂȂ�̂ŁA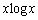 �̍ŏ��l�ׂĂ݂܂��B
�̍ŏ��l�ׂĂ݂܂��B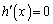 �Ƃ���ƁA
�Ƃ���ƁA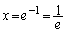
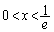 �ɂ�����
�ɂ�����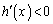 ���
���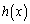 �͌����A
�͌����A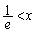 �ɂ�����
�ɂ�����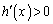 ���
���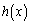 �͑����B
�͑����B����āA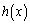 ��
��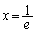 �ɂ����čŏ��l
�ɂ����čŏ��l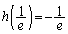 (
(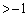 )���Ƃ�܂��B����āA
)���Ƃ�܂��B����āA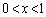 �ɂ����āA
�ɂ����āA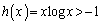
���ӂ�x�������āA
�� 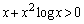 �ڕW�̕s���������藧���Ƃ������Ă��܂��܂����B
�ڕW�̕s���������藧���Ƃ������Ă��܂��܂����B
�܂��A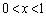 �ɂ�����s�����A
�ɂ�����s�����A �ɂ����āA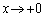 �Ƃ���ƁA
�Ƃ���ƁA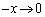 �ƂȂ�A�͂��݂����̌������A
�ƂȂ�A�͂��݂����̌������A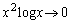
������A�@�ɂ����āA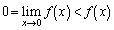 �ƂȂ�̂ŁA��͂�A
�ƂȂ�̂ŁA��͂�A �ƂȂ�܂��B�ł����A���̏ؖ���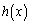 �̍ŏ��l���l���邱�Ƃɂ��A���ɂ���ł��܂��B(1)�̓��ĂƂ��ẮA�ȉ��̂悤�Ȃ��̂ɂȂ�ł��傤�B
�̍ŏ��l���l���邱�Ƃɂ��A���ɂ���ł��܂��B(1)�̓��ĂƂ��ẮA�ȉ��̂悤�Ȃ��̂ɂȂ�ł��傤�B
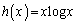 ���l����B
���l����B 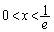 �ɂ�����
�ɂ�����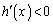 ���
���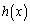 �͌����A
�͌����A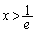 �ɂ�����
�ɂ�����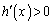 ���
���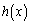 �͑����B
�͑����B
����āA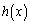 ��
��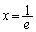 �ɂ����čŏ��l
�ɂ����čŏ��l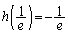 (
(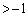 )���Ƃ�B����āA
)���Ƃ�B����āA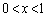 �ɂ����āA
�ɂ����āA���ӂ�x (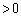 )�������āA
)�������āA �� 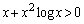 ��蕶�����������ōŏ�����ȏ�̂悤�ȓ��Ă������͓̂���Ǝv���܂����A
��蕶�����������ōŏ�����ȏ�̂悤�ȓ��Ă������͓̂���Ǝv���܂����A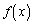 �̑�������
�̑�������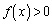 ���������߂ɂ́A�Ƃ����Ƃ��납��v�����A�[���Ɏ������ŊԂɍ����͂��ł��B
���������߂ɂ́A�Ƃ����Ƃ��납��v�����A�[���Ɏ������ŊԂɍ����͂��ł��B
(2) 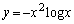
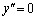 �Ƃ���ƁA
�Ƃ���ƁA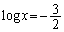 �C
�C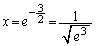
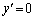 �Ƃ���ƁA
�Ƃ���ƁA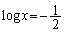 �C
�C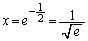
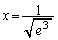 �̂Ƃ�
�̂Ƃ�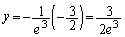 �C
�C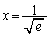 �̂Ƃ�
�̂Ƃ�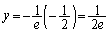
| x | 0 |
| 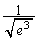 |
| 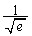 |
|
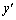 | �~ | �{ | �{ | �{ | 0 | �| |
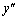 | �~ | �{ | 0 | �| | �| | �| |
| y | �~ |  | 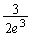 |  | 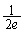 |  |
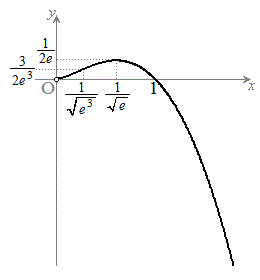 (1)�̌��ʂ��
(1)�̌��ʂ��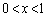 �ɂ�����
�ɂ�����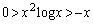 �C�����ŁA
�C�����ŁA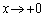 �Ƃ����
�Ƃ����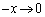 �C�͂��݂����̌������
�C�͂��݂����̌������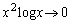 �C����āA
�C����āA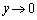
�����\(���̑����A���̉������Q��)���A�O���t�͉E�}����(���}���͏���)�B
�NjL�D��L�Ɠ��l�ɁA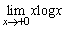 �����ɂȂ邱�Ƃ�����܂��B��L�Ɠ����悤�ɂ�낤�Ƃ��āA
�����ɂȂ邱�Ƃ�����܂��B��L�Ɠ����悤�ɂ�낤�Ƃ��āA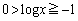 �̊e�ӂ�x��������
�̊e�ӂ�x��������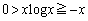 �̌`�ł͂��݂����Ɏ����������Ƃ��Ă��A
�̌`�ł͂��݂����Ɏ����������Ƃ��Ă��A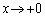 �̂Ƃ�
�̂Ƃ�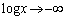 �Ȃ̂ŁA���������A
�Ȃ̂ŁA���������A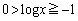 �Ƃ����s�������������܂���B
�Ƃ����s�������������܂���B �����ŁA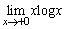 �ł́A
�ł́A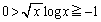 �̊e�ӂ�
�̊e�ӂ�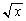 �������邱�Ƃ��l���܂��B�܂��A
�������邱�Ƃ��l���܂��B�܂��A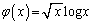 �̍ŏ��l�ׂ܂��B
�̍ŏ��l�ׂ܂��B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B