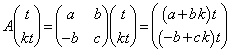�x�R��㐔�w'10�N[3]
�s�� �ŕ\�������W���ʏ�̓_�̈ړ����l����B���_��ʂ钼��l��̂��ׂĂ̓_��l��Ɉڂ����Ƃ��A���̈ړ��ɂ����l�͂��ꎩ�g�Ɉڂ����Ƃ������Ƃɂ���B���̂Ƃ��A���̖₢�ɓ�����B
�ŕ\�������W���ʏ�̓_�̈ړ����l����B���_��ʂ钼��l��̂��ׂĂ̓_��l��Ɉڂ����Ƃ��A���̈ړ��ɂ����l�͂��ꎩ�g�Ɉڂ����Ƃ������Ƃɂ���B���̂Ƃ��A���̖₢�ɓ�����B
(1) ���_��ʂ钼���ŁA���̈ړ��ɂ���Ă��ꎩ�g�Ɉڂ������̂����傤��2���݂��邽�߂̕K�v�\��������a�Cb�Cc��p���ĕ\���B
(2) a�Cb�Cc��(1)�̏������݂����Ƃ��A(1)��2�̒����́A����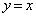 �Ɋւ��đΏ̂ł��邱�Ƃ��ؖ�����B
�Ɋւ��đΏ̂ł��邱�Ƃ��ؖ�����B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@1���ϊ��̖��ł��Bx���ɐ����Ȓ����ƁA�����łȂ�����(�X�������݂��钼��)�ɕ����čl���܂��B
(1)(i) ���ꎩ�g�Ɉڂ���钼���� �̂Ƃ��A
�̂Ƃ��A ���� ��̓_�́At��C�ӂ̎����Ƃ��āA
��̓_�́At��C�ӂ̎����Ƃ��āA �ƕ\���܂��B
�ƕ\���܂��B ���ꂪ�A�Ăђ���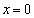 ��̓_�ł��邽�߂ɁA
��̓_�ł��邽�߂ɁA ����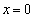 ��̂��ׂĂ̓_�ɂ��āA�܂�C�ӂ̎���t�ɂ��āA���ꂪ���藧���߂ɁA
��̂��ׂĂ̓_�ɂ��āA�܂�C�ӂ̎���t�ɂ��āA���ꂪ���藧���߂ɁA 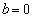 �@����@
�@����@���K�v�ł��B
�t��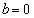 �̂Ƃ��A�܂�A
�̂Ƃ��A�܂�A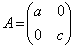 �̂Ƃ��A
�̂Ƃ��A
���� �ȊO�ɂ����ꎩ�g�Ɉڂ���钼��
�ȊO�ɂ����ꎩ�g�Ɉڂ���钼��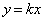 �����݂���Ƃ��܂��B
�����݂���Ƃ��܂��B
����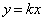 ��̓_�́At��C�ӂ̎����Ƃ��āA
��̓_�́At��C�ӂ̎����Ƃ��āA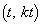 �ƕ\����܂��B
�ƕ\����܂��B ���ꂪ�A�Ăђ���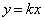 ��̓_�ł��邽�߂ɁA
��̓_�ł��邽�߂ɁA ����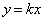 ��̂��ׂĂ̓_�ɂ��āA�܂�C�ӂ̎���t�ɂ��āA���ꂪ���藧���߂ɁA
��̂��ׂĂ̓_�ɂ��āA�܂�C�ӂ̎���t�ɂ��āA���ꂪ���藧���߂ɁA ���K�v�ł����A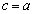 �̂Ƃ��A�܂�A
�̂Ƃ��A�܂�A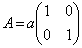 �̂Ƃ��A
�̂Ƃ��A �ƂȂ�A�C�ӂ̎���k�ɂ��āA���� �����ꎩ�g�Ɉڂ���钼���ƂȂ�A�u���傤��2���݂���v�Ƃ������������܂���B�]���āA
�����ꎩ�g�Ɉڂ���钼���ƂȂ�A�u���傤��2���݂���v�Ƃ������������܂���B�]���āA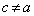 �ł����A���̂Ƃ��́A�A���A
�ł����A���̂Ƃ��́A�A���A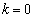 (������
(������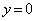 )�ƂȂ�A�ړ�A�ɂ���Ă��ꎩ�g�Ɉڂ���钼�������傤��2�A����
)�ƂȂ�A�ړ�A�ɂ���Ă��ꎩ�g�Ɉڂ���钼�������傤��2�A����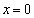 �ƒ���
�ƒ���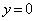 �����݂��܂��B����āA�@�ƍ��킹�āA���̏ꍇ���K�v�\�������́A
�����݂��܂��B����āA�@�ƍ��킹�āA���̏ꍇ���K�v�\�������́A 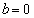 ����
����  �@����B
�@����B(ii) ���ꎩ�g�Ɉڂ���钼����2�{�Ƃ� �̌`�����Ă���Ƃ��A
�̌`�����Ă���Ƃ��A ����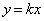 ��̓_�́At��C�ӂ̎����Ƃ��āA
��̓_�́At��C�ӂ̎����Ƃ��āA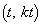 �ƕ\����܂����A
�ƕ\����܂����A ���ꂪ�A�Ăђ���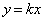 ��̓_�ł��邽�߂ɁA
��̓_�ł��邽�߂ɁA ����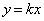 ��̂��ׂĂ̓_�ɂ��āA�܂�C�ӂ̎���t�ɂ��āA���ꂪ���藧���߂ɁA
��̂��ׂĂ̓_�ɂ��āA�܂�C�ӂ̎���t�ɂ��āA���ꂪ���藧���߂ɁA 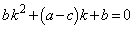 �@����C
�@����C���ꎩ�g�Ɉڂ���钼�������傤��2�{���݂��邽�߂ɁA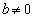 (
(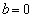 �̂Ƃ��͇C��2���������ɂȂ�܂���)�ł����Ă��A�����̌X��k��2�ʂ葶�݂���A�܂�A2���������C���قȂ�������������Ƃ��K�v�\���ł��B����āA
�̂Ƃ��͇C��2���������ɂȂ�܂���)�ł����Ă��A�����̌X��k��2�ʂ葶�݂���A�܂�A2���������C���قȂ�������������Ƃ��K�v�\���ł��B����āA �B�C�D�����킹�āA(i)�C(ii)���A���߂�K�v�\�������́A
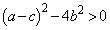 ......[��]
......[��]
(2) a�Cb�Cc��(1)�̏������݂����Ƃ��A�܂��A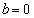 �̂Ƃ��A�܂�B�̂Ƃ��A���ꎩ�g�Ɉڂ���钼���́A����
�̂Ƃ��A�܂�B�̂Ƃ��A���ꎩ�g�Ɉڂ���钼���́A����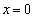 �ƒ���
�ƒ��� �ł���2�����́A����
�ł���2�����́A����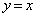 �Ɋւ��đΏ̂ł��B
�Ɋւ��đΏ̂ł��B  �̏ꍇ�́A�����̌X��k�́A���قȂ�2��������L����2���������C�����܂��B2���������C��2����
�̏ꍇ�́A�����̌X��k�́A���قȂ�2��������L����2���������C�����܂��B2���������C��2����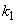 �C
�C �Ƃ���ƁA���ƌW���̊W���A
�Ƃ���ƁA���ƌW���̊W���A����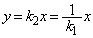 �C����
�C����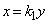 �ƒ���
�ƒ��� �́A����
�́A����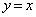 �Ɋւ��đΏ̂ł��B(�ؖ��I)
�Ɋւ��đΏ̂ł��B(�ؖ��I)
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B