日本女子大理数学'11年前期[3]
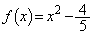とおく。
(1) 2次方程式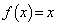
の2つの解をα，β (
)とする。α，β の値を求めよ。 (2)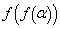 
の値を求めよ。 (3) 関数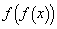
を求めよ。 (4) 方程式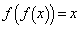
を解け。
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
解答 (2)を活かして考えれば(4)は容易です。
(1) 
より、
......[答]
(3) 
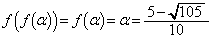......[答]
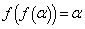と合わせて、
は、方程式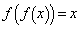
の解にもなっています。
従って、
は、
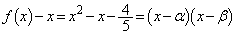で割り切れます(因数定理を参照)。除算を実行する(整式の除算を参照)と、商が
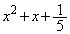となり、の解は、
解は、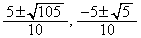
......[答]
追記．本問だけであれば容易ですが、本問には以下のような類題があります。
一橋大'97年後期[1]
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
aは0と異なる実数とし、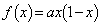
とおく。 (1) 
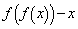は、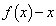
で割り切れることを示せ。 (2) 
，
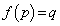をみたす異なる実数p，qが存在するようなaの値の範囲を求めよ。 【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
解答(1)は、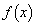
の具体的な形が与えられていなくても示すことが可能です。なお、'97年には、岡山大[2]にも類題が出題されています。
(1) 2次方程式
の解を、
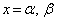とします。 です。よって、4次方程式
は、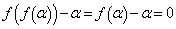 
，
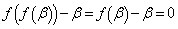
より、やはり、解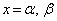
をもちます。よって、
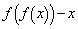は、
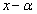でも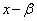
でも割り切れます。従って、
は
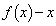で割り切れます。
(2) 
，
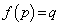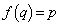より、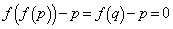 
，
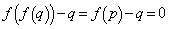
よって、p，qは、方程式
の解です。ですが、 
，
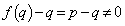
より、p，qは、方程式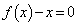
の解ではありません。 これより、p，qは、
の2解であり、この2次方程式が相異なる2実数解p，qをもつために、判別式について、
∴ 
，
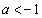......[答]
数学TOP TOPページに戻る
各問題の著作権は
出題大学に属します。©2005-2024(有)りるらる 苦学楽学塾 随時入会受付中！理系大学受験ネット塾苦学楽学塾(ご案内はこちら)ご入会は、
まず、こちらまでメールを
お送りください。 
の解が
であることにより、
の解が
であることにより、
の解が、
の解が、
