��s�嗝�n���w'11�N�O��[2]
���W��Ԃ�3�_A �CB
�CB �CC
�CC ��ʂ镽�ʂ�α�Ƃ���B�_D
��ʂ镽�ʂ�α�Ƃ���B�_D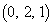 ��ʂ�A�x�N�g��
��ʂ�A�x�N�g��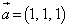 �ɕ��s�Ȓ�����
�ɕ��s�Ȓ����� �Ƃ���B�܂��A�_D��ʂ�A�x�N�g��
�Ƃ���B�܂��A�_D��ʂ�A�x�N�g��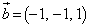 �ɕ��s�Ȓ�����
�ɕ��s�Ȓ����� �Ƃ���B���̂Ƃ��A�ȉ��̖₢�ɓ�����B
�Ƃ���B���̂Ƃ��A�ȉ��̖₢�ɓ�����B
(1) 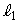 ��α�̌�_��E�Ƃ��A
��α�̌�_��E�Ƃ��A ��α�Ƃ̌�_��F�Ƃ���BE�CF�̍��W�����߂�B
��α�Ƃ̌�_��F�Ƃ���BE�CF�̍��W�����߂�B (2)  ��
��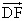 �̂Ȃ��p��θ (
�̂Ȃ��p��θ (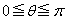 )�Ƃ���Ƃ��A
)�Ƃ���Ƃ��A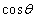 �̒l�����߂�B
�̒l�����߂�B (3) ��DEF�̖ʐς����߂�B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@���ʂ̕������𗘗p����Α債�����Ƃ͂Ȃ��̂ł����A���p���Ȃ��A�Ƃ������ƂɂȂ�ƁA���ʓ|�ɂȂ�܂��B�Ȃ��A��ԃx�N�g�����Q�Ƃ��Ă��������B
(1) 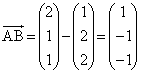 �C
�C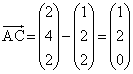
����α��̓_ �́Ap�Cq�������Ƃ��āA
�́Ap�Cq�������Ƃ��āA 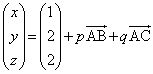 �@����@
�@����@�ƕ\�����Ƃ��ł��܂��B�����ŁA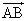 �C
�C �o���ɐ����ȃx�N�g��
�o���ɐ����ȃx�N�g��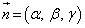 �������邱�Ƃ��ł����Ƃ��āA�@���ӂ�
�������邱�Ƃ��ł����Ƃ��āA�@���ӂ�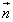 �Ƃ̓��ς��l����ƁA
�Ƃ̓��ς��l����ƁA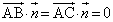 ���A
���A �� 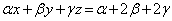 �@����A
�@����A
�Ƃ����W�������藧���܂��B���̊W����α�̕������ƌ����܂��B�����ŁA �����߂邱�Ƃɂ��܂��B
�����߂邱�Ƃɂ��܂��B 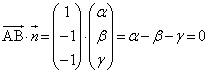 �@����B
�@����B
 �@����C
�@����C�C���A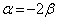 �C������B�ɑ�����āA
�C������B�ɑ�����āA 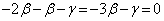 �@��
�@�� 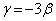
����āA
�Ƃ���A �́A
�́A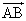 �C
�C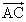 �o���ɐ����ɂȂ�܂��B����
�o���ɐ����ɂȂ�܂��B���� ���A����α�̖@���x�N�g���ƌ����܂��B�@���x�N�g���͕����݂̂��d�v�ŁA
���A����α�̖@���x�N�g���ƌ����܂��B�@���x�N�g���͕����݂̂��d�v�ŁA �̑傫���͏d�v�ȗv�f�ł͂Ȃ��̂ŁA
�̑傫���͏d�v�ȗv�f�ł͂Ȃ��̂ŁA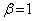 �Ƃ��āA
�Ƃ��āA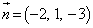 �Ƃ��܂��B���̂Ƃ��A�A�́A
�Ƃ��܂��B���̂Ƃ��A�A�́A 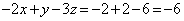 �@����D
�@����D�ƂȂ�܂��B
����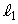 ��̓_
��̓_ �́A
�́A  �@����E
�@����E�ƕ\���܂��B����α��̓_�͇D�����̂ŁA������D�ɑ������ƁA
�� 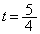 �E���AE�̍��W�́A
�E���AE�̍��W�́A ......[��]����
......[��]����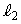 ��̓_
��̓_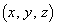 �́A
�́A 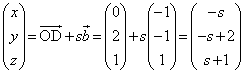 �@����F
�@����F�ƕ\���܂��B������D�ɑ������ƁA
�� 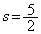 �F���AF�̍��W�́A
�F���AF�̍��W�́A ......[��]
......[��]
���A
 ......[��]
......[��]
(3) ��DEF�̖ʐς́A
�NjL�D��L�ŁA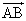 �C
�C �̑o���ɐ����ȃx�N�g���́A�O���𗘗p����A
�̑o���ɐ����ȃx�N�g���́A�O���𗘗p����A �Ƌ��߂邱�Ƃ��ł��܂��B���Ăɂ́A �ƂȂ鎖���������Ă����Ηǂ��ł��傤�B
�ƂȂ鎖���������Ă����Ηǂ��ł��傤�B
���ʂ̕������𗘗p���Ȃ��ꍇ�ɂ́A����α��̓_ ���A
���A �������Ƃ𗘗p���܂��B�E���A����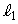 ��̓_
��̓_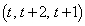 ���G�������Ƃ���A
���G�������Ƃ���A ���A
��A�����āAE�̍��W�����߂邱�ƂɂȂ�܂��BF�̍��W�����l�ł��B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B 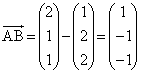 �C
�C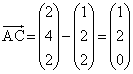
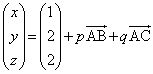 �@����@
�@����@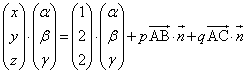
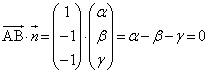 �@����B
�@����B �@����C
�@����C �@����E
�@����E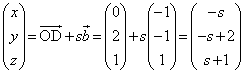 �@����F
�@����F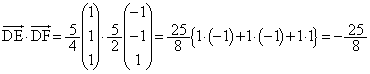
 ......[��]
......[��]
