名古屋市大芸工数学'11年[4]
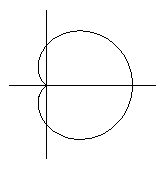 xy平面上において、媒介変数t (
xy平面上において、媒介変数t (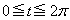 )によって
)によって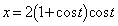 ,
,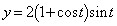 と表される右図の曲線について次の問いに答えよ。
と表される右図の曲線について次の問いに答えよ。
(1) xの最大値、最小値を求めよ。
(2) 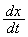 を求めよ。
を求めよ。 (3) この曲線で囲まれる図形をx軸のまわりに1回転してできる立体の体積を求めよ。
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
解答 曲線はカージオイドです。媒介変数表示された曲線を回転させたときの回転体体積の問題です。大変な計算になりそうに見えますが、やってみると意外と簡単です。
(1) 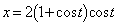
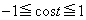 より、
より、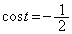 ,つまり、
,つまり、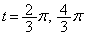 のときに、最小値:
のときに、最小値: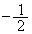 ......[答]
......[答]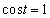 ,つまり、
,つまり、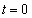 のときに、最大値:4 ......[答]
のときに、最大値:4 ......[答]
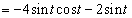 ......[答]
......[答]
(3) 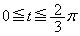 (
(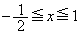 )における曲線のy座標を
)における曲線のy座標を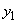 ,
,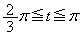 (
(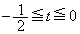 )における曲線のy座標を
)における曲線のy座標を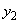 とします。立体の体積Vは、
とします。立体の体積Vは、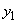 を回転させた回転体の体積から、
を回転させた回転体の体積から、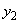 を回転させた回転体の体積を引いたものです(x軸のまわりの回転体を参照)。
を回転させた回転体の体積を引いたものです(x軸のまわりの回転体を参照)。 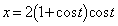 とおくと、(2)より
とおくと、(2)より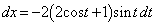
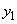 では、x:
では、x: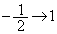 のときt:
のときt: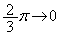 ,
,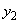 では、x:
では、x: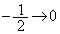 のときt:
のときt: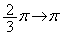 (置換積分を参照)
(置換積分を参照)
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
数学TOP TOPページに戻る
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
各問題の著作権は
出題大学に属します。©2005-2024(有)りるらる 苦学楽学塾 随時入会受付中!理系大学受験ネット塾苦学楽学塾(ご案内はこちら)ご入会は、
まず、こちらまでメールを
お送りください。