���k�嗝�n���w'11�N�O��[5]
a�������Az��0�łȂ����f���Ƃ���Bz�Ƌ����ȕ��f���� �ŕ\���B
�ŕ\���B
(1) ������z�����߂�B
(2) ������z�����݂���悤��a�͈̔͂����߂�B
(3) ������z�����݂���悤��a�͈̔͂����߂�B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@���f���̖��Ǝv������A(2)(3)�͎����̖��ł����B
(1) �^����z�������܂��B
�A���A�^����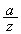 ���܂ނ̂ŁA
���܂ނ̂ŁA �����ɂȂ邱�Ƃ͂Ȃ��A
�����ɂȂ邱�Ƃ͂Ȃ��A �ł��B
�ł��B
�@��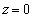 �Ƃ����������Ƃ���ƁA
�Ƃ����������Ƃ���ƁA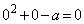 ���
���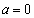
(i) 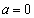 �̂Ƃ��A�@�́A
�̂Ƃ��A�@�́A 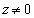 ���A
���A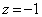
(ii) 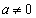 �̂Ƃ��A�@�̉��́A
�̂Ƃ��A�@�̉��́A ����āA ......[��]
......[��]
(2) �^����z�������܂��B
 �@����A
�@����Au�Cv�������Ƃ��āA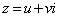 �Ƃ����ƁA
�Ƃ����ƁA �ł��B
�ł��B ����́A���ĕ��f�����ʂ������͈͂ɓ����Ă����Ƃ��ɁA
�ƂȂ��Ă��������ɑ��Ȃ�܂���B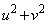 �͎����Ȃ̂ŁA
�͎����Ȃ̂ŁA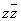 �͎����ł��B�]���āA
�͎����ł��B�]���āA ���Az�͎����Ɍ����A
���Az�͎����Ɍ����A �ł��B�A�́A
�ł��B�A�́A  �@����B
�@����B�ƂȂ�܂��B�A���A�^����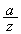 ���܂ނ̂ŁA
���܂ނ̂ŁA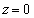 �������ɂȂ邱�Ƃ͂Ȃ��A
�������ɂȂ邱�Ƃ͂Ȃ��A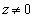 �ł��B
�ł��B
�A��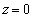 �Ƃ����������Ƃ����
�Ƃ����������Ƃ����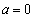
(i) 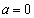 �̂Ƃ��A�A�́A
�̂Ƃ��A�A�́A 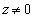 ���A
���A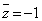 �C�����A
�C�����A �ŁA�A����z (
�ŁA�A����z (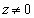 )�����݂��܂��B
)�����݂��܂��B(ii) 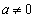 �̂Ƃ��A�B��z��2���������Ƃ݂�Ƃ��A������z�����݂��邽�߂ɁA
�̂Ƃ��A�B��z��2���������Ƃ݂�Ƃ��A������z�����݂��邽�߂ɁA ���ʎ��F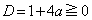
�ȏ���A�^������z�����݂���a�͈̔͂́A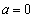 ���܂߂āA
���܂߂āA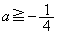 ......[��]
......[��]
(3) �^����z�������܂��B
 �@����B
�@����Bu�Cv�������Ƃ��āA �Ƃ����ƁA
�Ƃ����ƁA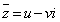 �ł��B
�ł��B 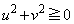 ���A
���A �Ƃ����ƁAx�͎�����
�Ƃ����ƁAx�͎�����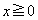 �ł��B������A�B�́A
�ł��B������A�B�́A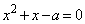 �@����C
�@����C�ƂȂ�܂��B�A���A�^���� ���܂ނ̂ŁA
���܂ނ̂ŁA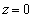 �����ɂȂ邱�Ƃ͂Ȃ��A
�����ɂȂ邱�Ƃ͂Ȃ��A �ł��B�]����
�ł��B�]����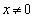 �ł��B
�ł��B
������^������z�����݂���Ƃ��A�C�� �͈̔͂ɉ��������܂��B���̏����́A
�͈̔͂ɉ��������܂��B���̏����́A �Ƃ��āA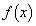 �̃O���t�̎���
�̃O���t�̎���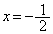 (
(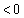 )�ł��邱�Ƃ���A
)�ł��邱�Ƃ���A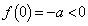 �C�����A
�C�����A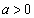 ......[��] �@(2���������̈�ʘ_���Q��)
......[��] �@(2���������̈�ʘ_���Q��)
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B  ......[��]
......[��]