山形大医数学'11年[1]
座標平面において、点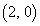 を中心とする半径2の円をCとする。点
を中心とする半径2の円をCとする。点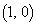 を通る直線
を通る直線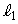 と円Cとの交点をA,Bとし、点
と円Cとの交点をA,Bとし、点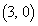 を通る直線
を通る直線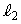 と円Cとの交点をP,Qとする。さらに、
と円Cとの交点をP,Qとする。さらに、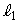 と
と は垂直に交わるとする。ただし、
は垂直に交わるとする。ただし、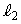 は座標軸とは一致しない。
は座標軸とは一致しない。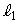 の傾きをkで表す。このとき、次の問いに答えよ。
の傾きをkで表す。このとき、次の問いに答えよ。
(1) 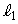 と
と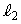 の交点Dは円Cの内部にあることを示せ。
の交点Dは円Cの内部にあることを示せ。 (2) 弦ABの長さをkを用いて表せ。
(3) 弦PQの長さをkを用いて表せ。
(4) 四角形APBQの面積の最大値を求めよ。
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
解答 (2),(3)は、半径rの円が直線から切り取る弦の長さが、円の中心と直線との距離をdとして、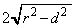 (∵ 三平方の定理)となることを使って求めます。なお、円と直線の位置関係を参照してください。
(∵ 三平方の定理)となることを使って求めます。なお、円と直線の位置関係を参照してください。
(1) 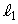 ,
, は、それぞれ定点を通る直線で、直交するので、交点は、2定点
は、それぞれ定点を通る直線で、直交するので、交点は、2定点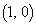 ,
,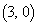 を直径の両端とする円周
を直径の両端とする円周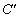 上にあります。
上にあります。 は円Cの内部に位置するので、
は円Cの内部に位置するので、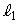 ,
,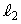 の交点Dは円Cの内部の点です。
の交点Dは円Cの内部の点です。
弦ABの長さは、
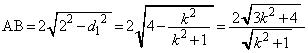 ......[答]
......[答]
弦PQの長さは、
 ......[答]
......[答]
(4) 四角形APBQの面積Sは、
Sは、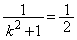 、つまり、
、つまり、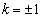 のとき、最大値:7 ......[答]
のとき、最大値:7 ......[答]
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
数学TOP TOPページに戻る
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
各問題の著作権は
出題大学に属します。©2005-2024(有)りるらる 苦学楽学塾 随時入会受付中!理系大学受験ネット塾苦学楽学塾(ご案内はこちら)ご入会は、
まず、こちらまでメールを
お送りください。 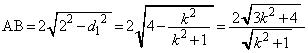 ......[答]
......[答]
 ......[答]
......[答]