��嗝�n���w'13�N�O��[2]
�s����
�̕\���̈��xy���ʂɐ}������B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@�f���ɏꍇ�������Ă��܂���16�ʂ�ɕ����邱�ƂɂȂ�܂����A����ł́A�������Ŏ��ԓI�Ɍ������Ȃ�܂��B
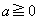 �C
�C �Ƃ��܂��B
�Ƃ��܂��B
 �C
�C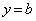 �̂Ƃ��^�s��������������Ƃ��܂��B�܂�A
�̂Ƃ��^�s��������������Ƃ��܂��B�܂�A
 �@����@
�@����@
 �^�s�����ŁA
�^�s�����ŁA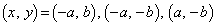 �Ƃ��Ă��@�Ɠ����ɂȂ�A�^�s�����͐������܂�(�����̐�Βl���Q��)�B
�Ƃ��Ă��@�Ɠ����ɂȂ�A�^�s�����͐������܂�(�����̐�Βl���Q��)�B
���l�ɁA �C
�C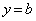 �̂Ƃ��^�s�������������Ȃ��Ƃ���ƁA
�̂Ƃ��^�s�������������Ȃ��Ƃ���ƁA �̂Ƃ��ɂ��^�s�����͐������܂���B
�̂Ƃ��ɂ��^�s�����͐������܂���B
�]���āA��1�ی��ŗ̈�D�����߂Ă����A�̈�D��y���Ɋւ��đΏ̂ȗ̈�C�̈�D�ƌ��_�Ɋւ��đΏ̂ȗ̈�A�̈�D��x���Ɋւ��đΏ̂ȗ̈���^�s�������\���̈�ƂȂ�܂��B
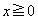 �C
�C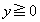 �̂Ƃ��A
�̂Ƃ��A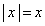 �C
�C ���A�^�s�����́A
���A�^�s�����́A
�ƂȂ�܂��B
(i) 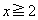 �C
�C �̂Ƃ��A�^�s�����́A
�̂Ƃ��A�^�s�����́A �� 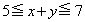
(ii) 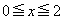 �C
�C �̂Ƃ��A�^�s�����́A
�̂Ƃ��A�^�s�����́A �� 
(iii) 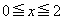 �C
�C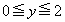 �̂Ƃ��A�^�s�����́A
�̂Ƃ��A�^�s�����́A �� 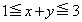
(iv)  �C
�C �̂Ƃ��A�^�s�����́A
�̂Ƃ��A�^�s�����́A �� 
(i)�`(iv)��}��������̈�D�́A�E��}���ΐF���F��(���E�����܂�)�B
�����y���Ɋւ��đΏ̂ȗ̈�A���_�Ɋւ��đΏ̂ȗ̈�Ax���Ɋւ��đΏ̂ȗ̈�����킹�āA���߂�̈�͉E���}���ΐF���F��(���E�����܂�)�B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B