��嗝�n���w'24�N�O��[5]
���R��1�C2�C3�C����Cn�̂����An�ƌ݂��ɑf�ł�����̂̌���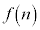 �Ƃ���B
�Ƃ���B
(1) ���R��a�Cb�Cc����ё��قȂ�f��p�Cq�Cr�ɑ��āA����
�����藧���Ƃ������B
(2) 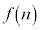 ��n�̖ƂȂ�5�ȏ�100�ȉ��̎��R��n�����ׂċ��߂�B
��n�̖ƂȂ�5�ȏ�100�ȉ��̎��R��n�����ׂċ��߂�B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@p�Cq�Cr��f���Aa�Cb�Cc�����R���Ƃ��āA�f����������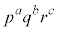 �ƂȂ鐮���̖́A
�ƂȂ鐮���̖́A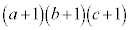 ����܂�(�������Q��)�B�{��ł́A�݂��ɑf�Ȏ��R���̌����l���܂��B
����܂�(�������Q��)�B�{��ł́A�݂��ɑf�Ȏ��R���̌����l���܂��B
(1) �܂��A�f��2��p�Cq (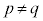 )�ɂ��f��������
)�ɂ��f��������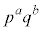 (a�Cb�͎��R��)���l���܂��B1�C2�C3�C����C
(a�Cb�͎��R��)���l���܂��B1�C2�C3�C����C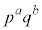 �̂���
�̂���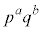 �ƌ݂��ɑf�Ȃ��̂́A1�C2�C3�C����C
�ƌ݂��ɑf�Ȃ��̂́A1�C2�C3�C����C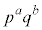 ����Ap�̔{���ƁAq�̔{�������������̂ł��B�A���Ap�̔{����q�̔{���ɂ͏d��������܂��B
����Ap�̔{���ƁAq�̔{�������������̂ł��B�A���Ap�̔{����q�̔{���ɂ͏d��������܂��B 1�C2�C3�C����C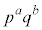 ��v�f�Ƃ���W����C�CC�̗v�f�̂���p�̔{���ł���W����A�CC�̗v�f�̂���q�̔{���ł���W����B�Ƃ��āCC�̗v�f�̂���p�̔{���ł����Ă���q�̔{���ł���W��
��v�f�Ƃ���W����C�CC�̗v�f�̂���p�̔{���ł���W����A�CC�̗v�f�̂���q�̔{���ł���W����B�Ƃ��āCC�̗v�f�̂���p�̔{���ł����Ă���q�̔{���ł���W��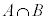 ��
��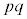 �̔{���̏W���ł��B�����ŁA
�̔{���̏W���ł��B�����ŁA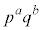 �́Ap�̔{���ł�����Aq�̔{���ł�����A
�́Ap�̔{���ł�����Aq�̔{���ł�����A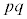 �̔{���ł�����܂��B����āA
�̔{���ł�����܂��B����āA ���R��a�Cb�Cc����ё��قȂ�f��p�Cq�Cr�ɑ��āA1�C2�C3�C����C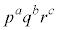 �̂���
�̂���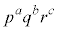 �ƌ݂��ɑf�Ȃ��̂́A1�C2�C3�C����C
�ƌ݂��ɑf�Ȃ��̂́A1�C2�C3�C����C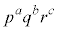 ����Ap�̔{���ƁAq�̔{���ƁAr�̔{�������������̂ł��B�A���Ap�̔{����q�̔{���ɂ͏d��������
����Ap�̔{���ƁAq�̔{���ƁAr�̔{�������������̂ł��B�A���Ap�̔{����q�̔{���ɂ͏d��������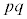 �̔{���ł��Bq�̔{����r�̔{���ɂ��d��������
�̔{���ł��Bq�̔{����r�̔{���ɂ��d��������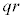 �̔{���ł��Br�̔{����p�̔{���ɂ��d��������
�̔{���ł��Br�̔{����p�̔{���ɂ��d��������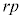 �̔{���ł��B�܂��A
�̔{���ł��B�܂��A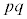 �̔{����
�̔{����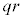 �̔{����
�̔{����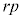 �̔{���ɂ��d��������
�̔{���ɂ��d��������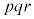 �̔{���ł��B1�C2�C3�C����C
�̔{���ł��B1�C2�C3�C����C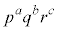 ��v�f�Ƃ���W����D�CD�̗v�f�̂���p�̔{���ł���W����A�CD�̗v�f�̂���q�̔{���ł���W����B�CD�̗v�f�̂���r�̔{���̏W����C�Ƃ��āC
��v�f�Ƃ���W����D�CD�̗v�f�̂���p�̔{���ł���W����A�CD�̗v�f�̂���q�̔{���ł���W����B�CD�̗v�f�̂���r�̔{���̏W����C�Ƃ��āC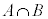 ��
��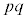 �̔{���̏W���A
�̔{���̏W���A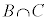 ��
��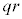 �̔{���̏W���A
�̔{���̏W���A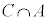 ��
��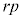 �̔{���̏W���A
�̔{���̏W���A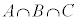 ��
��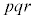 �̔{���̏W���ł��B
�̔{���̏W���ł��B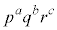 ��p�̔{���ł�����Aq�̔{���ł�����Ar�̔{���ł�����A
��p�̔{���ł�����Aq�̔{���ł�����Ar�̔{���ł�����A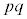 �̔{���ł�����A
�̔{���ł�����A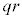 �̔{���ł�����A
�̔{���ł�����A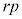 �̔{���ł�����A
�̔{���ł�����A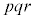 �̔{���ł�����܂��B
�̔{���ł�����܂��B 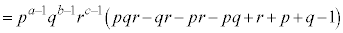
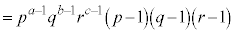 �@����A
�@����A
(2) �f����������������4������ƁA2�C3�C5�C7�Ȃ̂ŁA�f��4�ɂ��f���������ɂȂ鎩�R���ōŏ��̂��̂́A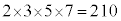 ��100���傫���A100�ȉ��̎��R���́A3�ȉ��̑f���őf���������ł��܂��B
��100���傫���A100�ȉ��̎��R���́A3�ȉ��̑f���őf���������ł��܂��B
�f��3�ɂ��f���������ƂȂ鎩�R���������������炠����ƁA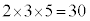 �C
�C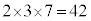 �C
�C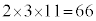 �C
�C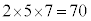 �C
�C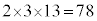 �C
�C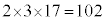 �C
�C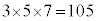 �ƂȂ�A����ȊO�͂��ׂ�100���傫���Ȃ�܂��B100�ȉ��̎��R���őf����������3�̑f���ɂ����̂ł́A�f����������
�ƂȂ�A����ȊO�͂��ׂ�100���傫���Ȃ�܂��B100�ȉ��̎��R���őf����������3�̑f���ɂ����̂ł́A�f����������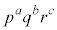 �Ƃ��āA���ׂ�
�Ƃ��āA���ׂ�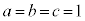 �ł��B�܂�A3�̑f���̐ςƂ��ĕ\����鎩�R���ɂȂ�܂��B���R��1�C2�C3�C����C
�ł��B�܂�A3�̑f���̐ςƂ��ĕ\����鎩�R���ɂȂ�܂��B���R��1�C2�C3�C����C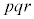 �̂����A
�̂����A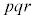 �ƌ݂��ɑf�Ȏ��R���̌��́A�A���A
�ƌ݂��ɑf�Ȏ��R���̌��́A�A���A p�Cq�Cr�͑f���ŁA3�̑f���̂����ɂ�2�ȊO�̑f��������A�Ⴆ�A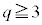 �Ƃ���ƁAq�͊�ŋ���
�Ƃ���ƁAq�͊�ŋ���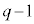 (
(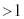 )�̔{���ɂȂ蓾���A
)�̔{���ɂȂ蓾���A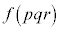 ��
��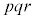 �̖ɂȂ邱�Ƃ͂���܂���B100�ȉ��̎��R���őf����������2�̑f��p�Cq (
�̖ɂȂ邱�Ƃ͂���܂���B100�ȉ��̎��R���őf����������2�̑f��p�Cq (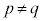 )�ɂ����̂ł́Aa�Cb�����R���A�f����������
)�ɂ����̂ł́Aa�Cb�����R���A�f����������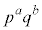 �C
�C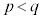 �Ƃ��āA�@���A
�Ƃ��āA�@���A �E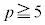 �C
�C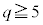 �̂Ƃ��A����
�̂Ƃ��A����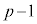 �C
�C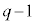 �́A�
�́A�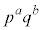 �̖ɂȂ蓾���A
�̖ɂȂ蓾���A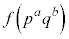 ��
��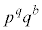 �̖ɂȂ蓾�܂���B
�̖ɂȂ蓾�܂���B �E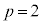 �C
�C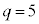 �̂Ƃ��A
�̂Ƃ��A ����́A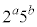 �̖ɂȂ蓾�܂���(
�̖ɂȂ蓾�܂���(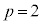 �Ȃ̂�
�Ȃ̂�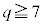 �ł����A�ȉ���
�ł����A�ȉ���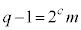 �̏ꍇ�Ɋ܂܂�܂�)�B
�̏ꍇ�Ɋ܂܂�܂�)�B �E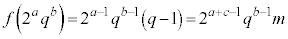 �C
�C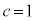 �̂Ƃ��Aq����Ȃ̂ŁAc�����R���Am����Ƃ��āA
�̂Ƃ��Aq����Ȃ̂ŁAc�����R���Am����Ƃ��āA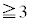 �ƕ\���܂����A
�ƕ\���܂����A 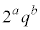 �̏ꍇ�Am��3�ȏ�̊�ł����Am ��
�̏ꍇ�Am��3�ȏ�̊�ł����Am ��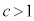 �̖ł��f��q�̖ł��Ȃ�(
�̖ł��f��q�̖ł��Ȃ�(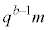 )�A
)�A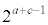 �́A
�́A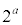 �̖ɂȂ蓾�܂���B
�̖ɂȂ蓾�܂���B
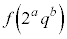 �̏ꍇ�A
�̏ꍇ�A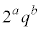 ���
���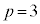 ��
��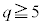 �̖łȂ��A����
�̖łȂ��A����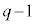 �͊
�͊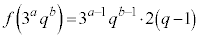 �̖ł��Ȃ��A
�̖ł��Ȃ��A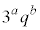 �́A
�́A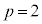 �̖ɂȂ蓾�܂���B
�̖ɂȂ蓾�܂���B�E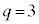 �C
�C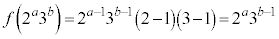 �̂Ƃ��Aq�͊�Ȃ̂�
�̂Ƃ��Aq�͊�Ȃ̂�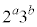 �͋����ł���A
�͋����ł���A �͋����Ȃ̂ŁA��ł���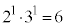 �̖ɂȂ蓾�܂���B
�̖ɂȂ蓾�܂���B �ȏ���A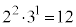 �C
�C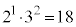 �Ɍ����܂��B
�Ɍ����܂��B �́Aa�Cb�������Ȃ鎩�R���ł����Ă��A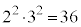 �̖ł��B5�ȏ�100�ȉ��̎��R���ŁA�f����������
�̖ł��B5�ȏ�100�ȉ��̎��R���ŁA�f����������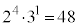 (a�Cb�͎��R��)�̌`�ɂȂ鎩�R���́A
(a�Cb�͎��R��)�̌`�ɂȂ鎩�R���́A �ł��B
�f����������1�̑f��p�ɂ����̂ł́A�f����������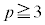 ���Ƃ��āAp�̔{����
���Ƃ��āAp�̔{����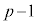 �ƌ݂��ɑf�ł͂���܂���B
�ƌ݂��ɑf�ł͂���܂���B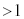 �ȉ���p�̔{����
�ȉ���p�̔{����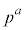 ����܂��B
����܂��B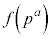 �ƌ݂��ɑf�Ȏ��R���́A
�ƌ݂��ɑf�Ȏ��R���́A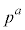 ����܂��B
����܂��B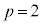 �̂Ƃ��Ap�͑f���ł����Ȃ̂ŁA����
�̂Ƃ��Ap�͑f���ł����Ȃ̂ŁA����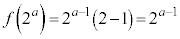 (
(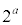 )��
)��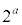 �̖ɂ͂Ȃ蓾���A
�̖ɂ͂Ȃ蓾���A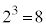 ��
��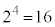 �̖ł͂���܂���B
�̖ł͂���܂���B
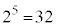 �̂Ƃ��A
�̂Ƃ��A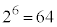 �́Aa�������Ȃ鎩�R���ł����Ă��A
�́Aa�������Ȃ鎩�R���ł����Ă��A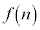 �̖ł��B5�ȏ�100�ȉ��̎��R���ŁA�f����������
�̖ł��B5�ȏ�100�ȉ��̎��R���ŁA�f����������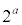 (a�͎��R��)�̌`�ɂȂ鎩�R���́A
(a�͎��R��)�̌`�ɂȂ鎩�R���́A �ł��B
�B�C�C���A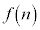 ��n�̖ƂȂ�5�ȏ�100�ȉ��̎��R��n�́A
��n�̖ƂȂ�5�ȏ�100�ȉ��̎��R��n�́A 6�C8�C12�C16�C18�C24�C32�C36�C48�C54�C64�C72�C96 ......[��]
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B 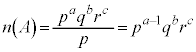
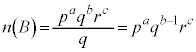
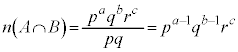
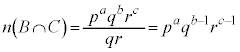
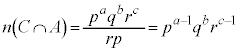
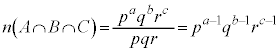
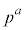 ����܂��B
����܂��B