東京科学大医歯学系2025年数学入試問題
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
[1] 20個の合同な正三角形の面を持ち、各頂点に5つの面が集まるへこみのない多面体を、正二十面体という。各面に20種類の異なる目が1つずつ与えられており、すべての目が等しい確率で出る正二十面体のサイコロをIとする。Iの2つの面A，Bに対し、Iの表面上を、Aの内部の点からBの内部の点へ、Iの頂点を通らずに移動するとき、横切るIの辺の本数の最小値を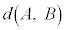
とする。たとえば、AとBが1辺を共有しているとき、
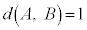となる。また、Iの任意の面Aに対し、
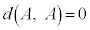とする。さらに、Iをn回投げたとき、i回目に出た目に対応する面を
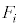とし、
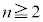のとき、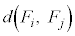
(
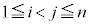)の最大値をM，最小値をmとする。このとき、以下の各問いに答えよ。
(1) xyz空間において、Iの1つの面とxy平面が平行となるようにIを配置したとき、Iの頂点または辺上の点を通りz軸に平行な直線とxy平面の交点全体の集合がなす図形を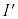
とする。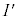
の概形を描け。ただし、
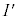における線分どうしの長さの比やなす角の角度は正確でなくてもよい。
(2) 
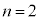のとき、0以上の整数kに対し、
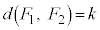となる確率を
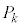とする。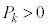
となるすべてのkに対して、それぞれ
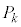を求めよ。
(3) 
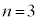のとき、
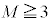となる確率を求めよ。
(4) 
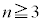のとき、
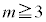となる確率を求めよ。
(5) 
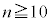のとき、
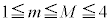となる確率を求めよ。 [解答へ]
[2] xy平面上に3点O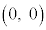
，A
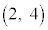，B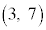
をとる。さらに、
となる整数m，nが存在するようなxy平面上の点P全体の集合をLとする。このとき、以下の各問いに答えよ。
(2) Lに属する点のうち、x軸上にあるものをすべて求めよ。
(3) 2点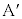
，
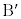をLの要素とする。Lの任意の要素Pに対して、
(4) 任意のLの要素Pに対して、内積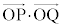
が整数となるようなxy平面上の点Q全体の集合をMとする。Mの要素のうち、x座標およびy座標の絶対値がともに1以下であるものをすべて求めよ。 [解答へ]
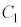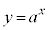[3] aを1より大きい実数とし、xy平面上の曲線
：
および曲線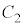
：
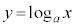について考える。原点をOとし、
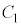上に点P，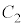
上に点Qをとる。このとき、以下の各問いに答えよ。
(1) Oを通る傾きkの直線が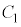
に接するとき、aの値をkを用いて表せ。また、接点の座標をaを用いて表せ。
(2) Oを通る直線が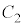
に接するとき、接点の座標をaを用いて表せ。
(3) △OPQが正三角形となるようなP，Qの組の個数を、aの値で場合分けして求めよ。
[解答へ]
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
東京科学大数学TOP 数学TOP TOPページに戻る
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
各問題の著作権は
出題大学に属します。なお、解答は、
苦学楽学塾制作です。©2005-2025(有)りるらる 苦学楽学塾 随時入会受付中！理系大学受験ネット塾苦学楽学塾(ご案内はこちら)ご入会は、
まず、こちらまでメールを
お送りください。 
，
，
はLに属するか。それぞれ判定せよ。
，
が存在するとき、
の最小値を求めよ。