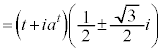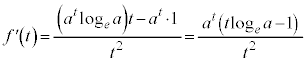�����Ȋw��㎕�w�n���w'25�N�O��[3]
a��1���傫�������Ƃ��Axy���ʏ�̋Ȑ�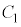 �F
�F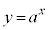 ����ыȐ�
����ыȐ�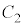 �F
�F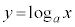 �ɂ��čl����B���_��O�Ƃ��A
�ɂ��čl����B���_��O�Ƃ��A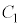 ��ɓ_P�C
��ɓ_P�C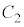 ��ɓ_Q���Ƃ�B���̂Ƃ��A�ȉ��̊e�₢�ɓ�����B
��ɓ_Q���Ƃ�B���̂Ƃ��A�ȉ��̊e�₢�ɓ�����B
(1) O��ʂ�X��k�̒�����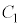 �ɐڂ���Ƃ��Aa�̒l��k��p���ĕ\���B�܂��A�ړ_�̍��W��a��p���ĕ\���B
�ɐڂ���Ƃ��Aa�̒l��k��p���ĕ\���B�܂��A�ړ_�̍��W��a��p���ĕ\���B
(2) O��ʂ钼����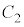 �ɐڂ���Ƃ��A�ړ_�̍��W��a��p���ĕ\���B
�ɐڂ���Ƃ��A�ړ_�̍��W��a��p���ĕ\���B
(3) ��OPQ�����O�p�`�ƂȂ�悤��P�CQ�̑g�̌����Aa�̒l�ŏꍇ�������ċ��߂�B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@��w���̓�����肾�������āA���G����ȓ��ł��B�{��ł͇G�̎���(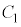 ��
��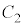 �͒���
�͒���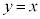 �Ɋւ��đΏ̂�P��Q��
�Ɋւ��đΏ̂�P��Q��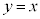 �Ɋւ��đΏ�)�ɋC�Â��Ȃ��Ƃ���グ�ɂȂ�܂��B
�Ɋւ��đΏ�)�ɋC�Â��Ȃ��Ƃ���グ�ɂȂ�܂��B
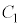 �ɌX��0�̐ڐ����������Ƃ͂ł��Ȃ��̂�
�ɌX��0�̐ڐ����������Ƃ͂ł��Ȃ��̂�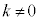 �ڐ��̌X����k���A
�ڐ��̌X����k���A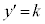 �Ƃ���
�Ƃ���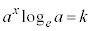 �C
�C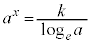
�ړ_��x���W��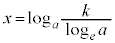 �C�ړ_��y���W��
�C�ړ_��y���W��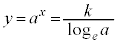 �@����@
�@����@
�ڐ��F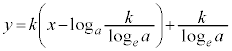
�ڐ��́A���_O��ʂ�̂ŁA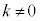 ���A
���A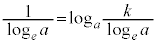 �C
�C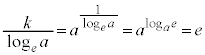 �C
�C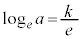 (�ΐ������Q��)�@��
(�ΐ������Q��)�@�� 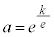 ......[��]�@�ɑ������ƁA
......[��]�@�ɑ������ƁA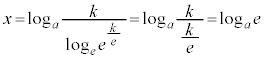 �C
�C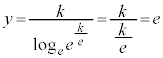
�ړ_�̍��W�́A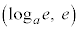 ......[��]
......[��]
�ڐ��̌X����k�C�����A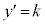 �Ƃ���
�Ƃ���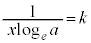
�ړ_��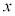 ���W��
���W��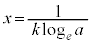 �C�ړ_��y���W��
�C�ړ_��y���W��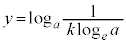 �@����A
�@����A
�ڐ��F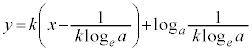
�ڐ��͌��_O��ʂ�̂ŁA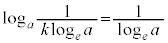 �C
�C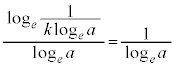 �C
�C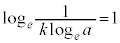 �C
�C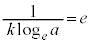
�A�ɑ������ƁA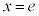 �C
�C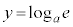
�ړ_�̍��W�́A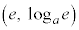 ......[��]
......[��]
(3) t�������C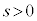 �Ƃ��āA
�Ƃ��āA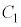 ��̓_P
��̓_P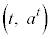 �C
�C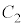 ��̓_Q
��̓_Q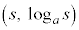 �ƌ��_O�ƂŐ��O�p�`�ƂȂ�̂ŁA
�ƌ��_O�ƂŐ��O�p�`�ƂȂ�̂ŁA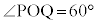 �ł��BP��
�ł��BP��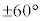 ��]������Q�ɗ��܂��B
��]������Q�ɗ��܂��B �܂��A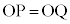 ���A
���A 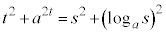
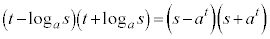 �@����B
�@����B�����ŁA
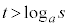 (�܂�
(�܂�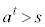 )�@����C
)�@����C�Ɖ��肷��ƁA�B�ɂ����āA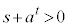 ���
���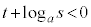 �C�����A
�C�����A 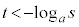 �@����D
�@����D�ł��B�C���D�Ƃ������Ƃ́A
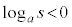 �@����E
�@����E�Ƃ������Ƃł��B����ƁA
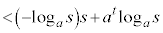 �@(�� �D)
�@(�� �D)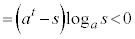 �@(�� �C�C�E)
�@(�� �C�C�E)�ƂȂ�A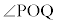 �͓݊p��
�͓݊p��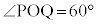 �ɂȂ蓾�܂���B�܂�A�C�̉���͔ے肳��܂�(�w���@�ɂ��Ă��ؖ��̋Z�I���Q��)�B
�ɂȂ蓾�܂���B�܂�A�C�̉���͔ے肳��܂�(�w���@�ɂ��Ă��ؖ��̋Z�I���Q��)�B 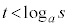 (�܂�
(�܂�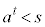 )�@����F
)�@����F�Ɖ��肷��ƁA�B�ɂ����āA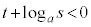 �C
�C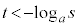 �ł���A
�ł���A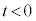 �ł��B
�ł��B 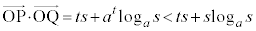 �@(�� �F)
�@(�� �F)��͂�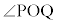 �͓݊p��
�͓݊p��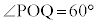 �ɂȂ蓾�܂���B�܂�A�F�̉���͔ے肳��܂��B
�ɂȂ蓾�܂���B�܂�A�F�̉���͔ے肳��܂��B
�C�C�F���Ƃ��ɔے肳���A�Ƃ������Ƃ́A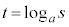 �Ƃ������Ƃł��B
�Ƃ������Ƃł��B
���̎����́A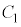 ��
��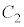 ���݂��ɋt���̊W�ɂ���A����
���݂��ɋt���̊W�ɂ���A����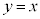 �Ɋւ��đΏ̂Ȃ̂ŁA��OPQ�����O�p�`�ɂȂ�Ƃ��A
�Ɋւ��đΏ̂Ȃ̂ŁA��OPQ�����O�p�`�ɂȂ�Ƃ��A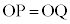 ���AP��Q�͒���
���AP��Q�͒���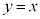 �Ɋւ��đΏ̂Ȉʒu�ɂ���A�Ώ̂łȂ��ꍇ�͐��O�p�`�ɂȂ�Ȃ��A�Ƃ������Ƃ��Ӗ����Ă��܂��B�܂�AP�CQ�̍��W�ɂ��āA
�Ɋւ��đΏ̂Ȉʒu�ɂ���A�Ώ̂łȂ��ꍇ�͐��O�p�`�ɂȂ�Ȃ��A�Ƃ������Ƃ��Ӗ����Ă��܂��B�܂�AP�CQ�̍��W�ɂ��āA 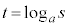 �C
�C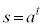 �@����G
�@����G���������܂��B
�ȉ��A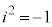 �C���������Ƃ��āA
�C���������Ƃ��āA 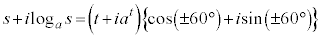 �@(�������{�̂Ƃ�P��
�@(�������{�̂Ƃ�P��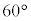 ��]�����Q�C�������|�̂Ƃ�P��
��]�����Q�C�������|�̂Ƃ�P��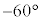 ��]�����Q)
��]�����Q)����āA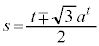 �@����H�C
�@����H�C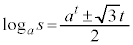 �@����I
�@����I
�H�ɂ����āA�������{�̂Ƃ��ɂ�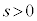 �ł����A�������|�̂Ƃ�(P��
�ł����A�������|�̂Ƃ�(P��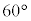 ��]�����Q)�ɂ́A
��]�����Q)�ɂ́A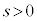 �ł��邽�߂�
�ł��邽�߂�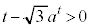 ���K�v�ł��B
���K�v�ł��B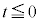 �Ȃ�
�Ȃ�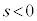 �ŕs�K�ł��B����āA
�ŕs�K�ł��B����āA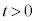 �ƂȂ�܂����A���̂Ƃ��A
�ƂȂ�܂����A���̂Ƃ��A 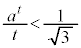 �@����J
�@����J�łȂ���Ȃ�܂���B
�G�C�H���A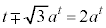 �C
�C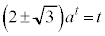
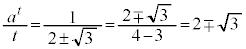 �@(�H�C�I���畡�������ł�)�@����K
�@(�H�C�I���畡�������ł�)�@����K�G�C�I���A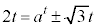 �C
�C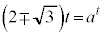 �C����͇K�Ɠ������ʂ�^���܂��B
�C����͇K�Ɠ������ʂ�^���܂��B
�����ŁA��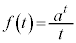 ���l���܂��B���������ƁA
���l���܂��B���������ƁA 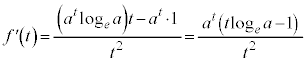
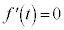 �Ƃ���ƁA
�Ƃ���ƁA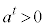 ���A
���A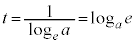
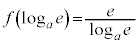 �C
�C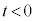 �̂Ƃ�
�̂Ƃ�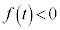 �ł����A
�ł����A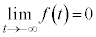 �C
�C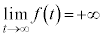 �C�����\�͈ȉ��̂悤�ɂȂ�܂��B
�C�����\�͈ȉ��̂悤�ɂȂ�܂��B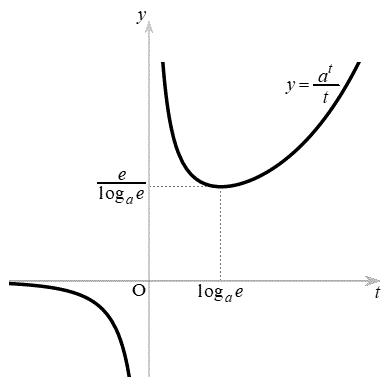
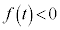 �ł�
�ł�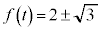 �ɂȂ蓾�Ȃ��̂ŁA
�ɂȂ蓾�Ȃ��̂ŁA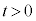 �ɂ�����ŏ��l
�ɂ�����ŏ��l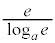 ��
��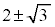 �̑召�ŕ��ނ��āA
�̑召�ŕ��ނ��āA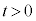 �ɂ����āA
�ɂ����āA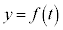 �̃O���t(�E�})�ƒ���
�̃O���t(�E�})�ƒ���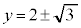 �̋��L�_�̌��ׂ܂�(�����@�̕������ւ̉��p(2)���Q��)�B���̌����A��OPQ�����O�p�`�ƂȂ�悤��P�CQ�̑g�̌��ɂȂ�܂��B
�̋��L�_�̌��ׂ܂�(�����@�̕������ւ̉��p(2)���Q��)�B���̌����A��OPQ�����O�p�`�ƂȂ�悤��P�CQ�̑g�̌��ɂȂ�܂��B
�Ƃ����(�ΐ������Q��)�A
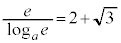 �̂Ƃ�
�̂Ƃ�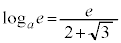 �C
�C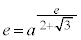 �C
�C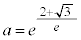 �ł��B
�ł��B
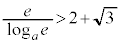 �̂Ƃ�
�̂Ƃ�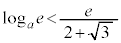 �C
�C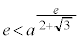 �C
�C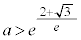 �ł��B
�ł��B
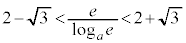 �̂Ƃ�
�̂Ƃ�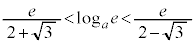 �C
�C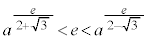 �C
�C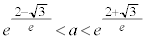 �ł��B
�ł��B
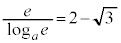 �̂Ƃ�
�̂Ƃ�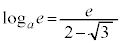 �C
�C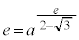 �C
�C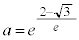 �ł��B
�ł��B
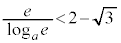 �̂Ƃ�
�̂Ƃ�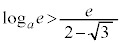 �C
�C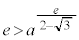 �C
�C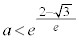 �ł��B
�ł��B
������A
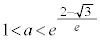 �̂Ƃ��A
�̂Ƃ��A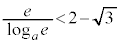 �ł����āA
�ł����āA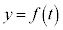 �̃O���t�́A
�̃O���t�́A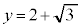 �C
�C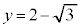 �̂�����Ƃ�2���L�_�������A��OPQ�����O�p�`�ƂȂ�悤��P�CQ�̑g�̌���4�ł��B
�̂�����Ƃ�2���L�_�������A��OPQ�����O�p�`�ƂȂ�悤��P�CQ�̑g�̌���4�ł��B
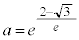 �̂Ƃ��A
�̂Ƃ��A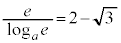 �ł����āA
�ł����āA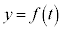 �̃O���t�́A
�̃O���t�́A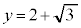 �Ƃ�2���L�_�������܂����A
�Ƃ�2���L�_�������܂����A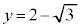 �Ƃ�1���L�_�����������A��OPQ�����O�p�`�ƂȂ�悤��P�CQ�̑g�̌���3�ł��B
�Ƃ�1���L�_�����������A��OPQ�����O�p�`�ƂȂ�悤��P�CQ�̑g�̌���3�ł��B
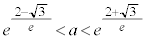 �̂Ƃ��A
�̂Ƃ��A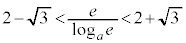 �ł����āA
�ł����āA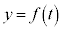 �̃O���t�́A
�̃O���t�́A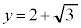 �Ƃ�2���L�_�������܂����C
�Ƃ�2���L�_�������܂����C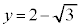 �Ƃ͋��L�_���������A��OPQ�����O�p�`�ƂȂ�悤��P�CQ�̑g�̌���2�ł��B
�Ƃ͋��L�_���������A��OPQ�����O�p�`�ƂȂ�悤��P�CQ�̑g�̌���2�ł��B
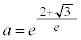 �̂Ƃ��A
�̂Ƃ��A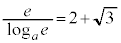 �ł����āA
�ł����āA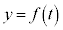 �̃O���t�́A
�̃O���t�́A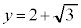 ��1���L�_�������C
��1���L�_�������C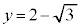 �Ƃ͋��L�_���������A��OPQ�����O�p�`�ƂȂ�悤��P�CQ�̑g�̌���1�ł��B
�Ƃ͋��L�_���������A��OPQ�����O�p�`�ƂȂ�悤��P�CQ�̑g�̌���1�ł��B
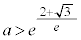 �̂Ƃ��A
�̂Ƃ��A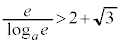 �ł����āA
�ł����āA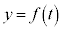 �̃O���t�́A
�̃O���t�́A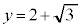 �C
�C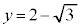 �̂�����Ƃ����L�_���������A��OPQ�����O�p�`�ƂȂ�悤��P�CQ�̑g�̌���0�ł��B
�̂�����Ƃ����L�_���������A��OPQ�����O�p�`�ƂȂ�悤��P�CQ�̑g�̌���0�ł��B
��L�ŁA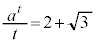 (
(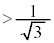 )�̂Ƃ��A�J�����Ȃ��悤�Ɍ����܂����A���̂Ƃ��H�̕����́{(P��
)�̂Ƃ��A�J�����Ȃ��悤�Ɍ����܂����A���̂Ƃ��H�̕����́{(P��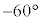 ��]�����Q)��
��]�����Q)��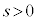 �ł��B
�ł��B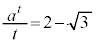 (
(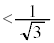 )�͇J�����Ă��܂�(���̂Ƃ��H�̕����́|��P��
)�͇J�����Ă��܂�(���̂Ƃ��H�̕����́|��P��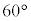 ��]�����Q)�B
��]�����Q)�B
�ȏ���A
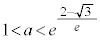 �̂Ƃ�4�C
�̂Ƃ�4�C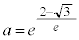 �̂Ƃ�3�C
�̂Ƃ�3�C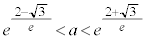 �̂Ƃ�2�C
�̂Ƃ�2�C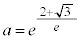 �̂Ƃ�1�C
�̂Ƃ�1�C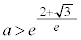 �̂Ƃ�0 ......[��]
�̂Ƃ�0 ......[��]
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@�����Ȋw�吔�wTOP�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B�Ȃ��A�́A
��w�y�w�m����ł��B©2005-2025(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B 
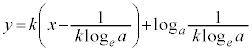
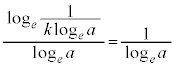 �C
�C