�����Ȋw��㎕�w�n���w'25�N�O��[1]
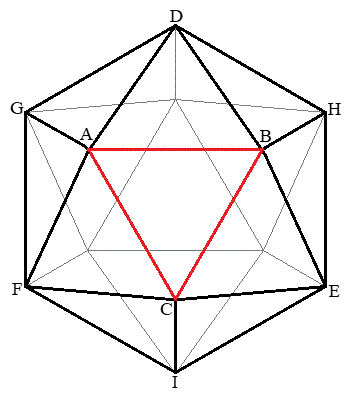
20�̍����Ȑ��O�p�`�̖ʂ������A�e���_��5�̖ʂ��W�܂�ւ��݂̂Ȃ����ʑ̂��A����\�ʑ̂Ƃ����B�e�ʂ�20��ނ̈قȂ�ڂ�1���^�����Ă���A���ׂĂ̖ڂ��������m���ŏo�鐳��\�ʑ̂̃T�C�R����I�Ƃ���BI��2�̖�A�CB�ɑ��AI�̕\�ʏ���AA�̓����̓_����B�̓����̓_�ցAI�̒��_��ʂ炸�Ɉړ�����Ƃ��A����I�̕ӂ̖{���̍ŏ��l��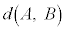 �Ƃ���B���Ƃ��AA��B��1�ӂ����L���Ă���Ƃ��A
�Ƃ���B���Ƃ��AA��B��1�ӂ����L���Ă���Ƃ��A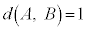 �ƂȂ�B�܂��AI�̔C�ӂ̖�A�ɑ��A
�ƂȂ�B�܂��AI�̔C�ӂ̖�A�ɑ��A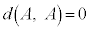 �Ƃ���B����ɁAI��n�����Ƃ��Ai��ڂɏo���ڂɑΉ�����ʂ�
�Ƃ���B����ɁAI��n�����Ƃ��Ai��ڂɏo���ڂɑΉ�����ʂ�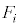 �Ƃ��A
�Ƃ��A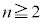 �̂Ƃ��A
�̂Ƃ��A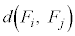 (
(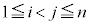 )�̍ő�l��M�C�ŏ��l��m�Ƃ���B���̂Ƃ��A�ȉ��̊e�₢�ɓ�����B
)�̍ő�l��M�C�ŏ��l��m�Ƃ���B���̂Ƃ��A�ȉ��̊e�₢�ɓ�����B
(1) xyz��Ԃɂ����āAI��1�̖ʂ�xy���ʂ����s�ƂȂ�悤��I��z�u�����Ƃ��AI�̒��_�܂��͕ӏ�̓_��ʂ�z���ɕ��s�Ȓ�����xy���ʂ̌�_�S�̂̏W�����Ȃ��}�`��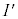 �Ƃ���B
�Ƃ���B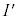 �̊T�`��`���B�������A
�̊T�`��`���B�������A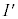 �ɂ���������ǂ����̒����̔��Ȃ��p�̊p�x�͐��m�łȂ��Ă��悢�B
�ɂ���������ǂ����̒����̔��Ȃ��p�̊p�x�͐��m�łȂ��Ă��悢�B
(2) 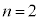 �̂Ƃ��A0�ȏ�̐���k�ɑ��A
�̂Ƃ��A0�ȏ�̐���k�ɑ��A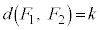 �ƂȂ�m����
�ƂȂ�m����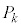 �Ƃ���B
�Ƃ���B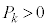 �ƂȂ邷�ׂĂ�k�ɑ��āA���ꂼ��
�ƂȂ邷�ׂĂ�k�ɑ��āA���ꂼ��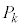 �����߂�B
�����߂�B
(3) 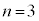 �̂Ƃ��A
�̂Ƃ��A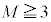 �ƂȂ�m�������߂�B
�ƂȂ�m�������߂�B
(4) 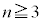 �̂Ƃ��A
�̂Ƃ��A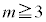 �ƂȂ�m�������߂�B
�ƂȂ�m�������߂�B
(5) 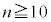 �̂Ƃ��A
�̂Ƃ��A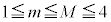 �ƂȂ�m�������߂�B
�ƂȂ�m�������߂�B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@���̊��o���������ł��B����������\�ʑ��̐}���`����Ă���킯�ł͂Ȃ��̂ŁA(1)���炵�đ�ςł��B
xy���ʂƕ��s�ł����āAI��xy���ʏ�ɂȂ�I�̈�̖ʂł��鐳�O�p�`����ABC(�E�}�ԐF�̕ӂň͂܂��O�p�`�A�܂�A��ԏ�ɗ��Ă��鐳�O�p�`)�Ƃ��܂��B�����ł͌����Ƃ��āA1��I�𓊂��ā�ABC�̈ʒu�ɂ���ʂ�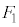 �Ƃ��Ai��I�𓊂��ďo���ڂɑΉ������
�Ƃ��Ai��I�𓊂��ďo���ڂɑΉ������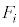 �́A��ABC�̈ʒu�ɂ���
�́A��ABC�̈ʒu�ɂ���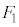 �ɑ��Ăǂ��Ɉʒu���邩�A�Ƃ������Ƃōl���܂��B�ȉ��ł́A�K�������AI�𓊂��Ĉ�ԏ�ɗ��Ă���ʂ���ABC�C
�ɑ��Ăǂ��Ɉʒu���邩�A�Ƃ������Ƃōl���܂��B�ȉ��ł́A�K�������AI�𓊂��Ĉ�ԏ�ɗ��Ă���ʂ���ABC�C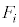 �Ƃ��čl���Ă���킯�ł͂Ȃ����Ƃɒ��ӂ��Ă��������B
�Ƃ��čl���Ă���킯�ł͂Ȃ����Ƃɒ��ӂ��Ă��������B
 (1) ��蕶�ł́A
(1) ��蕶�ł́A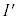 ���A�uI�̒��_�܂��͕ӏ�̓_��ʂ�z���ɕ��s�Ȓ�����xy���ʂ̌�_�S�̂̏W���v�Ƃ��Ă��܂����A����͐���\�ʑ�I�̂��ׂĂ̕ӁA���_��z�����������Ă��Ƃ���xy���ʂւ̓��e��
���A�uI�̒��_�܂��͕ӏ�̓_��ʂ�z���ɕ��s�Ȓ�����xy���ʂ̌�_�S�̂̏W���v�Ƃ��Ă��܂����A����͐���\�ʑ�I�̂��ׂĂ̕ӁA���_��z�����������Ă��Ƃ���xy���ʂւ̓��e��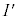 �Ƃ���A�Ƃ������Ƃł��B
�Ƃ���A�Ƃ������Ƃł��B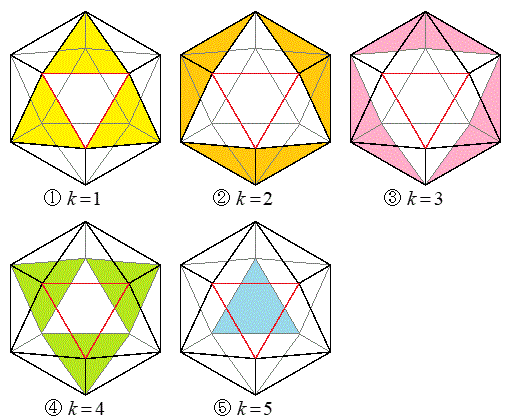 (2)
(2) 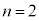 �̂Ƃ��A
�̂Ƃ��A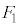 ���E�}�̐Ԑ��ň͂܂ꂽ���O�p�`���Ƃ����(�Ȍ�A
���E�}�̐Ԑ��ň͂܂ꂽ���O�p�`���Ƃ����(�Ȍ�A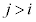 �Ƃ��āA����\�ʑ̂̃T�C�R����i��Cj�����Ƃ��A�u
�Ƃ��āA����\�ʑ̂̃T�C�R����i��Cj�����Ƃ��A�u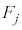 ��
��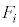 �Ɠ������O�p�`�v�Ƃ����̂́A
�Ɠ������O�p�`�v�Ƃ����̂́A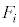 �ɗ^�����Ă���ڂƓ����ڂ̐��O�p�`��
�ɗ^�����Ă���ڂƓ����ڂ̐��O�p�`��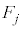 �ɂȂ�A�Ƃ����Ӗ��ł�)�A
�ɂȂ�A�Ƃ����Ӗ��ł�)�A
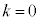 �C
�C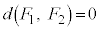 �ƂȂ�̂́A
�ƂȂ�̂́A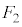 ��
��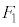 �Ɠ������O�p�`�ɂȂ�Ƃ��ŁA���̊m���́A
�Ɠ������O�p�`�ɂȂ�Ƃ��ŁA���̊m���́A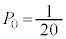
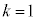 �C
�C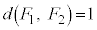 �ƂȂ�̂́A
�ƂȂ�̂́A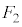 ���E�}�̇@�̉��F���F������3�̐��O�p�`�̂����ꂩ�ł���ꍇ�ŁA�����m���́A
���E�}�̇@�̉��F���F������3�̐��O�p�`�̂����ꂩ�ł���ꍇ�ŁA�����m���́A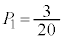
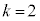 �C
�C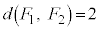 �ƂȂ�̂́A
�ƂȂ�̂́A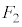 ���E�}�̇A�̞�F���F������6�̐��O�p�`�̂����ꂩ�ł���ꍇ�ŁA���̊m���́A
���E�}�̇A�̞�F���F������6�̐��O�p�`�̂����ꂩ�ł���ꍇ�ŁA���̊m���́A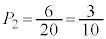
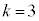 �C
�C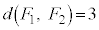 �ƂȂ�̂́A
�ƂȂ�̂́A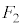 ���E�}�̇B�̃s���N�F���F��(DHEIFG�Ɋւ��ė����ɂȂ�܂�)����6�̐��O�p�`�̂����ꂩ�ł���ꍇ�ŁA���̊m���́A
���E�}�̇B�̃s���N�F���F��(DHEIFG�Ɋւ��ė����ɂȂ�܂�)����6�̐��O�p�`�̂����ꂩ�ł���ꍇ�ŁA���̊m���́A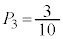
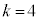 �C
�C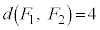 �ƂȂ�̂́A
�ƂȂ�̂́A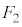 ���E�}�̇C�̉��ΐF���F��(����)����3�̐��O�p�`�̂����ꂩ�ł���ꍇ�ŁA���̊m���́A
���E�}�̇C�̉��ΐF���F��(����)����3�̐��O�p�`�̂����ꂩ�ł���ꍇ�ŁA���̊m���́A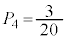
 �C
�C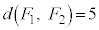 �ƂȂ�̂́A
�ƂȂ�̂́A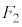 ���E�}�̇D�̐��F���F(����)�̐��O�p�`�ł���ꍇ�ŁA���̊m���́A
���E�}�̇D�̐��F���F(����)�̐��O�p�`�ł���ꍇ�ŁA���̊m���́A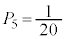
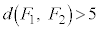 �ƂȂ邱�Ƃ͂���܂���B
�ƂȂ邱�Ƃ͂���܂���B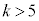 �̂Ƃ�
�̂Ƃ�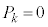 �ł��B
�ł��B
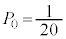 �C
�C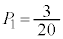 �C
�C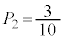 �C
�C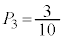 �C
�C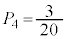 �C
�C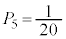 ......[��]
......[��]
(3) 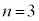 �̂Ƃ�
�̂Ƃ�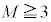 �ƂȂ�̂́A
�ƂȂ�̂́A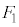 ���E��}�̐Ԑ��ň͂܂ꂽ���O�p�`�ł���Ƃ��āA
���E��}�̐Ԑ��ň͂܂ꂽ���O�p�`�ł���Ƃ��āA (i) 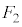 ���E��}�B�C�C�C�D(DHEIFG�Ɋւ��ė���)�̗̈���̐��O�p�`�C�܂�A
���E��}�B�C�C�C�D(DHEIFG�Ɋւ��ė���)�̗̈���̐��O�p�`�C�܂�A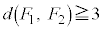 �ł���
�ł��� �܂���
(ii) 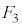 ���E��}�B�C�C�A�D�̗̈���̐��O�p�`�A�܂�A
���E��}�B�C�C�A�D�̗̈���̐��O�p�`�A�܂�A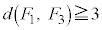 �ł���
�ł��� �܂���(iii) 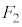 �C
�C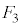 ���Ƃ��ɉE��}�@�C�A�̗̈���̐��O�p�`�ł����Ă��A
���Ƃ��ɉE��}�@�C�A�̗̈���̐��O�p�`�ł����Ă��A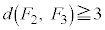 �ł���
�ł���
�ꍇ�ł��B�Ȃ��A(i)��(ii)�ɂ͏d��������܂��B(i)�C(ii)�̊m�����l����ƁA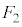 �܂���
�܂���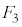 ���E��}�̇B�C�C�C�D�ɗ���ꍇ�ɂ�
���E��}�̇B�C�C�C�D�ɗ���ꍇ�ɂ�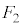 �C
�C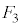 ���Ƃ��ɉE��}�̇B�C�C�C�D�ɗ���ꍇ���d������̂ŁA�����m���́A
���Ƃ��ɉE��}�̇B�C�C�C�D�ɗ���ꍇ���d������̂ŁA�����m���́A 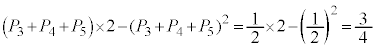 �@����E
�@����E(iii)�̏ꍇ�A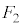 ��
��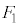 �ƈ�v���A�E��}�̐Ԑ��ň͂܂ꂽ��ABC�ɗ����Ƃ��ɂ́A
�ƈ�v���A�E��}�̐Ԑ��ň͂܂ꂽ��ABC�ɗ����Ƃ��ɂ́A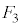 ���B�C�C�C�D�̗̈���̐��O�p�`�ɂ����
���B�C�C�C�D�̗̈���̐��O�p�`�ɂ����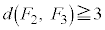 �ƂȂ�܂����A�����(ii)�̇E�Ɋ܂܂�܂��B
�ƂȂ�܂����A�����(ii)�̇E�Ɋ܂܂�܂��B
�܂��A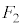 ����ABC�ɗאڂ��遢ABD�C��BCE�C��CAF(�E��}�̇@)�ɗ����Ƃ��A�Ⴆ��
����ABC�ɗאڂ��遢ABD�C��BCE�C��CAF(�E��}�̇@)�ɗ����Ƃ��A�Ⴆ��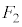 ����ABD�ɗ����Ƃ��A
����ABD�ɗ����Ƃ��A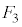 ���E��}�\��(�@�C�A)�́�CEI�CFI�ɗ��Ă�
���E��}�\��(�@�C�A)�́�CEI�CFI�ɗ��Ă�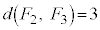 �ɂȂ�܂��B
�ɂȂ�܂��B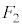 ����BCE�ɗ���ƁA
����BCE�ɗ���ƁA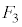 ����ADG�C��AFG�ɗ��Ă�
����ADG�C��AFG�ɗ��Ă�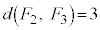 �ɂȂ�܂��B
�ɂȂ�܂��B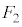 ����CAF�ɗ���ƁA
����CAF�ɗ���ƁA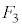 ����BDH�C��BEH�ɗ��Ă�
����BDH�C��BEH�ɗ��Ă�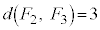 �ɂȂ�܂��B�����̊m���́A
�ɂȂ�܂��B�����̊m���́A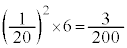 �@����F
�@����F
�܂��A�Ⴆ�A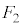 ����ADG�ɗ���ƁA
����ADG�ɗ���ƁA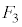 ���E��}�\��(�@�C�A)�́�BEH�C��BCE�C��CEI�C��CFI(4�ʂ�)�ɗ��Ă�
���E��}�\��(�@�C�A)�́�BEH�C��BCE�C��CEI�C��CFI(4�ʂ�)�ɗ��Ă�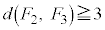 �ɂȂ�܂��B
�ɂȂ�܂��B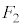 ���E��}�A��6�̐��O�p�`�̂ǂ��ɗ��Ă����l�ŁA�����̊m���́A
���E��}�A��6�̐��O�p�`�̂ǂ��ɗ��Ă����l�ŁA�����̊m���́A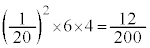 �@����G
�@����G
����āA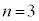 �̂Ƃ�
�̂Ƃ�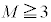 �ƂȂ�m���́A�E�C�F�C�G���A
�ƂȂ�m���́A�E�C�F�C�G���A 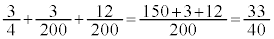 ......[��]
......[��]
(4) 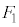 ���E��}�̐Ԑ��ň͂܂ꂽ���O�p�`�ł���Ƃ��܂��Bm��傫�����悤�Ƃ��āA
���E��}�̐Ԑ��ň͂܂ꂽ���O�p�`�ł���Ƃ��܂��Bm��傫�����悤�Ƃ��āA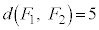 �C
�C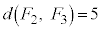 �̂悤�ɂ���ƁA
�̂悤�ɂ���ƁA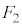 �͇D�ƂȂ�A
�͇D�ƂȂ�A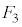 ��
��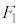 �Ɠ����O�p�`�ɖ߂��Ă��܂��A
�Ɠ����O�p�`�ɖ߂��Ă��܂��A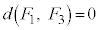 �C
�C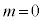 �ɂȂ��Ă��܂��܂��B�܂�A���x��I�𓊂���ƁA����ȑO�ɗ����ʒu�Ƌ߂��ʒu�ɖ߂��Ă��܂����Ƃ�����A
�ɂȂ��Ă��܂��܂��B�܂�A���x��I�𓊂���ƁA����ȑO�ɗ����ʒu�Ƌ߂��ʒu�ɖ߂��Ă��܂����Ƃ�����A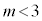 �ɂȂ��Ă��܂��܂��B
�ɂȂ��Ă��܂��܂��B 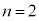 �̂Ƃ�
�̂Ƃ�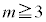 �ƂȂ邽�߂ɂ́A
�ƂȂ邽�߂ɂ́A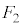 �́A�E��}�̇B�C�C�C�D�̗̈���̐��O�p�`�łȂ���Ȃ�܂���B�����ŁA
�́A�E��}�̇B�C�C�C�D�̗̈���̐��O�p�`�łȂ���Ȃ�܂���B�����ŁA�E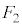 ���D���Ƃ���ƁA
���D���Ƃ���ƁA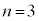 �̂Ƃ�
�̂Ƃ�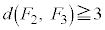 �ƂȂ邽�߂ɂ́A
�ƂȂ邽�߂ɂ́A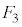 �͉E��}�\���ɗ���K�v������܂����A���̂Ƃ�
�͉E��}�\���ɗ���K�v������܂����A���̂Ƃ�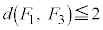 �ƂȂ�
�ƂȂ�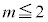 �ƂȂ��Ă��܂��܂��B
�ƂȂ��Ă��܂��܂��B 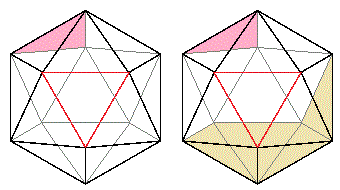 �E
�E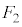 ���B��6�̐��O�p�`�̂ǂ����ɗ����Ƃ����
���B��6�̐��O�p�`�̂ǂ����ɗ����Ƃ����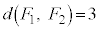 �ł��B
�ł��B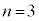 �̂Ƃ��A
�̂Ƃ��A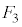 ���E��}�\���ɗ��Ă��܂���
���E��}�\���ɗ��Ă��܂���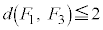 �ƂȂ�
�ƂȂ�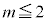 �ƂȂ��Ă��܂��܂��B�ł����A�Ⴆ��
�ƂȂ��Ă��܂��܂��B�ł����A�Ⴆ��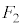 ���E�}�̃s���N�F�̐��O�p�`�̈ʒu�ɗ���ƁA
���E�}�̃s���N�F�̐��O�p�`�̈ʒu�ɗ���ƁA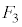 ���E�}�����F��4�̐��O�p�`�̂̂ǂ��炩�ɗ���A
���E�}�����F��4�̐��O�p�`�̂̂ǂ��炩�ɗ���A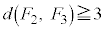 �ƂȂ�܂��B
�ƂȂ�܂��B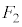 �C
�C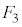 �����̏ƂȂ�m���́A
�����̏ƂȂ�m���́A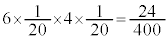 �@����I
�@����I����āA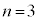 �̂Ƃ�
�̂Ƃ�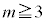 �ƂȂ�m���́A�H�C�I���A
�ƂȂ�m���́A�H�C�I���A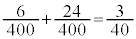 ......[��]
......[��]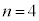 �̏ꍇ���l���܂��B
�̏ꍇ���l���܂��B �E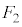 ���C��3�̉��ΐF�̐��O�p�`�̂ǂ����ɗ����Ƃ��܂��B�Ⴆ�A
���C��3�̉��ΐF�̐��O�p�`�̂ǂ����ɗ����Ƃ��܂��B�Ⴆ�A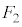 ���E��}�̉��ΐF�̐��O�p�`�ł����āA
���E��}�̉��ΐF�̐��O�p�`�ł����āA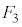 ���E��}�����F��2�̐��O�p�`�̂ǂ��炩���Ƃ��āA��L�I�Ɠ��l�ɍl����ƁA
���E��}�����F��2�̐��O�p�`�̂ǂ��炩���Ƃ��āA��L�I�Ɠ��l�ɍl����ƁA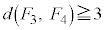 �ł���ʒu�́A�ǂ��
�ł���ʒu�́A�ǂ��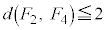 �ł�����
�ł�����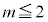 �ƂȂ��Ă��܂��܂��B
�ƂȂ��Ă��܂��܂��B 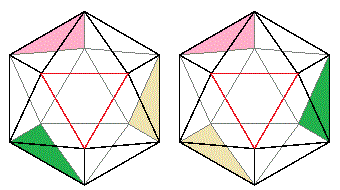 �E
�E ���B��6�̃s���N�F�̐��O�p�`�̂ǂ����ɗ����Ƃ��܂��B�Ⴆ�A
���B��6�̃s���N�F�̐��O�p�`�̂ǂ����ɗ����Ƃ��܂��B�Ⴆ�A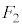 ���E�}�s���N�F�̐��O�p�`�ł����āA
���E�}�s���N�F�̐��O�p�`�ł����āA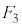 ���E��}�����F��4�̐��O�p�`�̂ǂꂩ���Ƃ��āA�Ⴆ�A�E�}��2�ʂ�̏��l����ƁA
���E��}�����F��4�̐��O�p�`�̂ǂꂩ���Ƃ��āA�Ⴆ�A�E�}��2�ʂ�̏��l����ƁA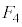 ���E�}�̗ΐF�̐��O�p�`�ɗ���A
���E�}�̗ΐF�̐��O�p�`�ɗ���A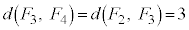 �ƂȂ�܂��B����2�ʂ�ȊO�ɂ́A
�ƂȂ�܂��B����2�ʂ�ȊO�ɂ́A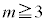 �ƂȂ�ꍇ�͂���܂���B����āA
�ƂȂ�ꍇ�͂���܂���B����āA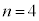 �̂Ƃ�
�̂Ƃ�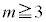 �ƂȂ�m���́A
�ƂȂ�m���́A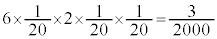 ......[��]
......[��]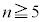 �̏ꍇ�ɂ́A
�̏ꍇ�ɂ́A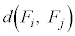 (
(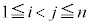 )�̂����ꂩ�̒���1��2�ɂȂ���̂�����A
)�̂����ꂩ�̒���1��2�ɂȂ���̂�����A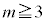 �ƂȂ蓾���A
�ƂȂ蓾���A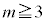 �ƂȂ�m����0 ......[��]
�ƂȂ�m����0 ......[��]
(5) 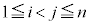 �̂Ƃ��A
�̂Ƃ��A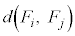 ��0����5�܂ł̐����l�݂̂Ƃ�̂ŁA
��0����5�܂ł̐����l�݂̂Ƃ�̂ŁA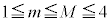 �ƂȂ�A�Ƃ������Ƃ́A
�ƂȂ�A�Ƃ������Ƃ́A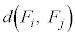 ��0�C5���Ƃ�Ȃ��A�Ƃ������Ƃł��B
��0�C5���Ƃ�Ȃ��A�Ƃ������Ƃł��B 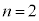 �̂Ƃ��A
�̂Ƃ��A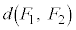 ��0�C5���Ƃ�Ȃ��A�Ƃ������Ƃ́A
��0�C5���Ƃ�Ȃ��A�Ƃ������Ƃ́A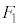 ��
��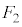 �ƈ�v�����A
�ƈ�v�����A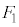 ���E��}�̇D�ɗ��邱�Ƃ��Ȃ�(
���E��}�̇D�ɗ��邱�Ƃ��Ȃ�(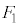 �̍s���
�̍s���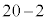 �ʂ�)�@����J
�ʂ�)�@����J
�Ƃ������Ƃł��B���̊m����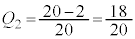 �ł��B
�ł��B
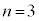 �̂Ƃ��A
�̂Ƃ��A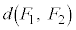 �C
�C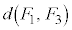 �C
�C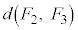 ��0�C5���Ƃ�Ȃ��A�Ƃ������Ƃ́A�J�ɉ����āA
��0�C5���Ƃ�Ȃ��A�Ƃ������Ƃ́A�J�ɉ����āA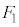 �C
�C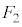 �͂Ƃ���
�͂Ƃ���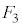 �ƈ�v�����A
�ƈ�v�����A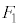 ��
��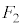 ���E��}�̇D�ɗ��邱�Ƃ͂Ȃ�(
���E��}�̇D�ɗ��邱�Ƃ͂Ȃ�(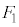 �C
�C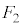 �̍s���
�̍s���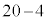 �ʂ�)�@����K
�ʂ�)�@����K
�Ƃ������Ƃł��B���̊m����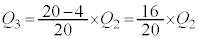 �ł��B
�ł��B
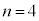 �̂Ƃ��A
�̂Ƃ��A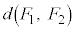 �C
�C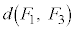 �C
�C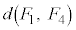 �C
�C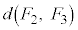 �C
�C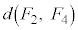 �C
�C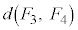 ��0�C5���Ƃ�Ȃ��A�Ƃ������Ƃ́A�K�ɉ����āA
��0�C5���Ƃ�Ȃ��A�Ƃ������Ƃ́A�K�ɉ����āA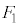 �C
�C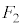 �C
�C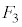 �͂������
�͂������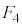 �ƈ�v�����A
�ƈ�v�����A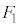 �C
�C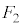 �C
�C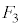 �͂�������E��}�̇D�ɗ��邱�Ƃ͂Ȃ�(
�͂�������E��}�̇D�ɗ��邱�Ƃ͂Ȃ�(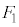 �C
�C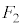 �C
�C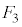 �̍s���
�̍s���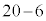 �ʂ�)�Ƃ������Ƃł��B���̊m����
�ʂ�)�Ƃ������Ƃł��B���̊m����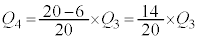 �ł��B
�ł��B
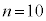 �̂Ƃ��A
�̂Ƃ��A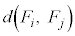 (
(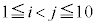 )�����ׂĂ�i�Cj�ɂ���0�C5���Ƃ�Ȃ��m���́A
)�����ׂĂ�i�Cj�ɂ���0�C5���Ƃ�Ȃ��m���́A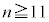 �̂Ƃ��A����\�ʑ̂ɂ�20�̖ʂ����Ȃ��̂ŁA
�̂Ƃ��A����\�ʑ̂ɂ�20�̖ʂ����Ȃ��̂ŁA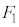 �`
�`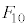 �̑S�Ă��A
�̑S�Ă��A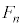 �ƈقȂ�A���A�E��}�̇D�ɗ��邱�Ƃ͂Ȃ��A�Ƃ������Ƃ͋N����܂���B���̂Ƃ��́A�m����0�ł��B
�ƈقȂ�A���A�E��}�̇D�ɗ��邱�Ƃ͂Ȃ��A�Ƃ������Ƃ͋N����܂���B���̂Ƃ��́A�m����0�ł��B
�ȏ���A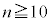 �̂Ƃ��A
�̂Ƃ��A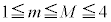 �ƂȂ�m���́A
�ƂȂ�m���́A
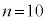 �̂Ƃ�
�̂Ƃ�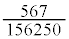 �C
�C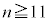 �̂Ƃ�0 ......[��]
�̂Ƃ�0 ......[��]
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@�����Ȋw�吔�wTOP�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B�Ȃ��A�́A
��w�y�w�m����ł��B©2005-2025(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B