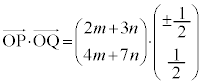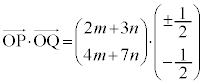�����Ȋw��㎕�w�n���w'25�N�O��[2]
xy���ʏ��3�_O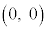 �CA
�CA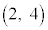 �CB
�CB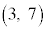 ���Ƃ�B����ɁA
���Ƃ�B����ɁA
�ƂȂ鐮��m�Cn�����݂���悤��xy���ʏ�̓_P�S�̂̏W����L�Ƃ���B���̂Ƃ��A�ȉ��̊e�₢�ɓ�����B
(1) 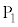
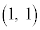 �C
�C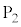
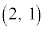 �C
�C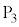
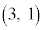 ��L�ɑ����邩�B���ꂼ�ꔻ�肹��B
��L�ɑ����邩�B���ꂼ�ꔻ�肹��B
(2) L�ɑ�����_�̂����Ax����ɂ�����̂����ׂċ��߂�B
(3) 2�_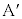 �C
�C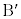 ��L�̗v�f�Ƃ���BL�̔C�ӂ̗v�fP�ɑ��āA
��L�̗v�f�Ƃ���BL�̔C�ӂ̗v�fP�ɑ��āA �ƂȂ鐮��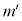 �C
�C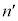 �����݂���Ƃ��A
�����݂���Ƃ��A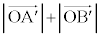 �̍ŏ��l�����߂�B
�̍ŏ��l�����߂�B
(4) �C�ӂ�L�̗v�fP�ɑ��āA����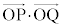 �������ƂȂ�悤��xy���ʏ�̓_Q�S�̂̏W����M�Ƃ���BM�̗v�f�̂����Ax���W�����y���W�̐�Βl���Ƃ���1�ȉ��ł�����̂����ׂċ��߂�B
�������ƂȂ�悤��xy���ʏ�̓_Q�S�̂̏W����M�Ƃ���BM�̗v�f�̂����Ax���W�����y���W�̐�Βl���Ƃ���1�ȉ��ł�����̂����ׂċ��߂�B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@�x�N�g����1���Ɨ������l�^�ɂ��������̖��ł��B�ȉ��̉�@�͂�┭���I��@�ł����AL�̗v�f�S�̂�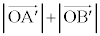 �̍ŏ��l���l����̂ł͑�ςł��B
�̍ŏ��l���l����̂ł͑�ςł��B
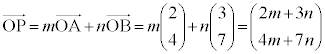 �@����@
�@����@
(1) 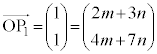 �Ƃ���ƁA
�Ƃ���ƁA 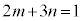 �@����A
�@����A
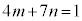 �@����B
�@����B�B�|�A�~2���A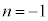 �C
�C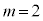
����m�Cn�����݂���̂ŁA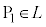
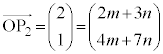 �Ƃ���ƁA
�Ƃ���ƁA 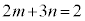 �@����C
�@����C
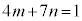 �@����D
�@����D�D�|�C�~2���A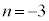 �C
�C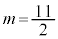 m�������łȂ��A
m�������łȂ��A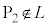
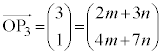 �Ƃ���ƁA
�Ƃ���ƁA 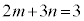 �@����E
�@����E
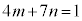 �@����F
�@����F�F�|�E�~2���A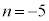 �C
�C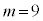
����m�Cn�����݂���̂ŁA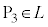
����āA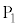
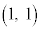 ��
��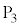
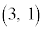 ��L�ɑ����邪�A
��L�ɑ����邪�A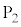
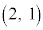 ��L�ɑ����Ȃ� ......[��]
��L�ɑ����Ȃ� ......[��]
(2) 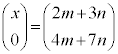 �Ƃ���ƁA
�Ƃ���ƁA
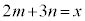 �@����G
�@����G
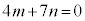 �@����H
�@����H�H���A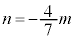 m��7�̔{���ŁAk�𐮐��Ƃ���
m��7�̔{���ŁAk�𐮐��Ƃ���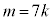 �Ƃ����ƁA
�Ƃ����ƁA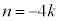
L�ɑ�����_�̂����Ax����ɂ�����̂́A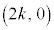 (k�F����) ......[��]
(k�F����) ......[��]
(3) L�̗v�fP�͕��ʏ�ɕ��z����̂ŁA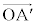 �C
�C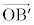 ��1���Ɨ��ł���K�v������܂��B�܂�A
��1���Ɨ��ł���K�v������܂��B�܂�A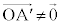 �C
�C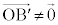 �ł���AO�C
�ł���AO�C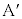 �C
�C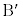 �͈꒼����ɂ͂���܂���B���̏�ŁA
�͈꒼����ɂ͂���܂���B���̏�ŁA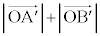 ���ŏ��Ƃ���
���ŏ��Ƃ���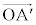 �C
�C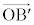 �����߂�̂ŁA
�����߂�̂ŁA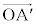 �C
�C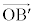 ��1���Ɨ��ł����āA�����_�̋߂��ɂ���
��1���Ɨ��ł����āA�����_�̋߂��ɂ���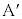 �C
�C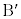 �����߂܂��B�����ŁAL�̗v�f�Ō��_O�̋߂��ɂ�����ׂ̂܂��B
�����߂܂��B�����ŁAL�̗v�f�Ō��_O�̋߂��ɂ�����ׂ̂܂��B (2)�Ɠ��l�ɂ��āA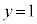 ��ɂ���L�̗v�f�ׂ܂��B
��ɂ���L�̗v�f�ׂ܂��B �ƂȂ�̂ŁA�J�|�K�Ƃ��āA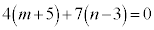 �@(���̉�@�ɂ��ẮA�s����������Q��)
�@(���̉�@�ɂ��ẮA�s����������Q��)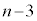 ��4�̔{���ŁAl�𐮐��Ƃ���
��4�̔{���ŁAl�𐮐��Ƃ���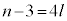 �Ƃ����ƁA
�Ƃ����ƁA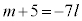
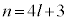 �C
�C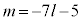
�I�ɑ������ƁA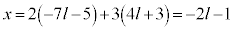 L�ɑ�����_�̂����A
L�ɑ�����_�̂����A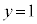 ��ɂ�����̂́A
��ɂ�����̂́A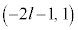 (l�F����)�@����L
(l�F����)�@����L
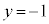 ��ɂ���L�̗v�f�ׂ܂��B
��ɂ���L�̗v�f�ׂ܂��B �ƂȂ�̂ŁA�N�|�O�Ƃ��āA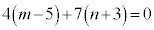
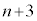 ��4�̔{���ŁAj�𐮐��Ƃ���
��4�̔{���ŁAj�𐮐��Ƃ���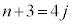 �Ƃ����ƁA
�Ƃ����ƁA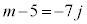
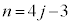 �C
�C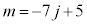
�M�ɑ������ƁA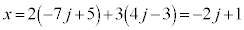 L�ɑ�����_�̂����A
L�ɑ�����_�̂����A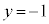 ��ɂ�����̂́A
��ɂ�����̂́A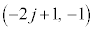 (j�F����)�@����P(2)�̌��ʂ��A
(j�F����)�@����P(2)�̌��ʂ��A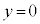 ���L�̗v�f�Ō��_�łȂ����_�ɋ߂����̂́A
���L�̗v�f�Ō��_�łȂ����_�ɋ߂����̂́A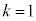 ��
��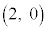 ��
��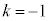 ��
��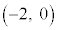 �ŁA���_�Ƃ̋�����2�ł��B
�ŁA���_�Ƃ̋�����2�ł��B
�L���A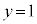 ���L�̗v�f�Ō��_�ɋ߂����̂́A
���L�̗v�f�Ō��_�ɋ߂����̂́A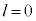 ��
��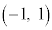 ��
��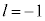 ��
��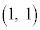 �ŁA���_�Ƃ̋�����
�ŁA���_�Ƃ̋�����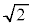 �ł��B
�ł��B
�P���A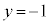 ���L�̗v�f�Ō��_�ɋ߂����̂́A
���L�̗v�f�Ō��_�ɋ߂����̂́A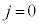 ��
��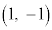 ��
��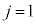 ��
��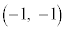 �ŁA���_�Ƃ̋�����
�ŁA���_�Ƃ̋�����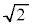 �ł��BL�̗v�f�ŁA
�ł��BL�̗v�f�ŁA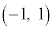 �C
�C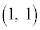 �C
�C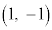 �C
�C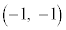 �������_O�ɋ߂����̂͂���܂���B
�������_O�ɋ߂����̂͂���܂���B
�����ŁA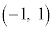 �C
�C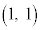 �C
�C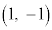 �C
�C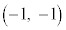 ��4�̂�������꒼����ɂȂ�2��I�т܂�(�ǂ̂悤�ɑI��ł��������ʂ�^���܂�)�B�Ⴆ�A
��4�̂�������꒼����ɂȂ�2��I�т܂�(�ǂ̂悤�ɑI��ł��������ʂ�^���܂�)�B�Ⴆ�A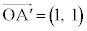 �C
�C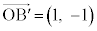 �Ƃ���ƁAL�̔C�ӂ̗v�f�͇@���m�Cn��C�ӂ̐����Ƃ��āA
�Ƃ���ƁAL�̔C�ӂ̗v�f�͇@���m�Cn��C�ӂ̐����Ƃ��āA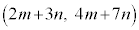 �Ƃ��ė^�����܂����A
�Ƃ��ė^�����܂����A �Ƃ��Ă݂�ƁA
�ӁX������ƁA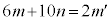 �@��
�@�� 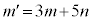 �C
�C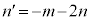
������A����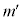 �C
�C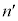 �����݂��܂��B
�����݂��܂��B
�ȏ���A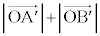 �̍ŏ��l��
�̍ŏ��l��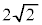 ......[��]
......[��]
(4) 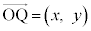 �C
�C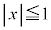 �C
�C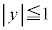 �Ƃ��܂��B�܂��A
�Ƃ��܂��B�܂��A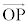 �Ƃ���L�̗v�f�ł��邱�Ƃ��m�F����Ă���A
�Ƃ���L�̗v�f�ł��邱�Ƃ��m�F����Ă���A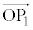 �C
�C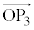 ���l���Ă݂܂��B
���l���Ă݂܂��B 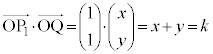 �@����Q�@(�������Q��)
�@����Q�@(�������Q��)k�͐����ł��B
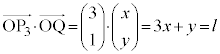 �@����R
�@����Rl�͐����ł��B
�R�|�Q���A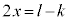 �͐����ł��B
�͐����ł��B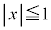 �������̂́A
�������̂́A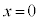 �C
�C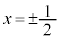 �C
�C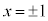 �ł��B
�ł��B
�R�|�Q�~3���A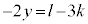 �͐����ł��B
�͐����ł��B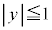 �������̂́A
�������̂́A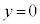 �C
�C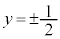 �C
�C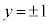 �ł��BL�̔C�ӂ̗v�f
�ł��BL�̔C�ӂ̗v�f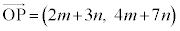 (m�Cn�͐���)�ɑ��āA
(m�Cn�͐���)�ɑ��āA
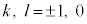 �Ƃ��āA
�Ƃ��āA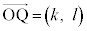 �̂Ƃ��A
�̂Ƃ��A �͐����ł��B
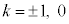 �Ƃ��āA
�Ƃ��āA
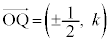 �̂Ƃ��A
�̂Ƃ��A 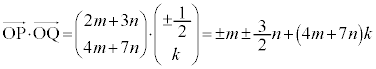 (��������)
(��������)��n����̂Ƃ������ɂȂ�܂���B
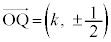 �̂Ƃ��A
�̂Ƃ��A 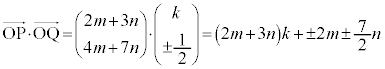 (��������)
(��������)��n����̂Ƃ������ɂȂ�܂���B
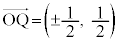 �̂Ƃ��A
�̂Ƃ��A 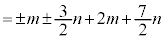 (��������)
(��������)�́A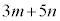 ��
��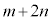 �ł����A������������ł��B
�ł����A������������ł��B
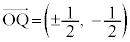 �̂Ƃ��A
�̂Ƃ��A 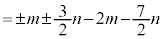 (��������)
(��������)�́A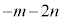 ��
��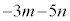 �ł����A������������ł��B
�ł����A������������ł��B
�ȏ���AM�̗v�f�̂����Ax���W�����y���W�̐�Βl���Ƃ���1�ȉ��ł�����̂́A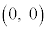 �C
�C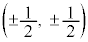 �C
�C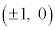 �C
�C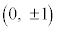 �C
�C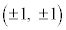 (�����C��) ......[��]
(�����C��) ......[��]
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@�����Ȋw�吔�wTOP�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B�Ȃ��A�́A
��w�y�w�m����ł��B©2005-2025(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B 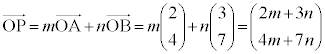 �@����@
�@����@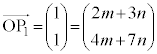 �Ƃ���ƁA
�Ƃ���ƁA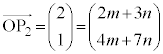 �Ƃ���ƁA
�Ƃ���ƁA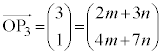 �Ƃ���ƁA
�Ƃ���ƁA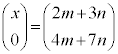 �Ƃ���ƁA
�Ƃ���ƁA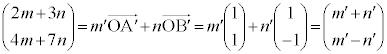
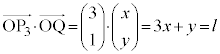 �@����R
�@����R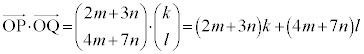
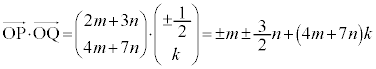 (��������)
(��������)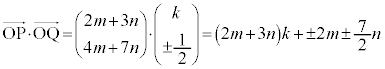 (��������)
(��������)