�ꋴ�吔�w'05�N�O��[4]
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
a��萔�Ƃ��Ax��2����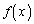 �C
�C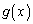 �����̂悤�ɒ�߂�B
�����̂悤�ɒ�߂�B
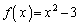 �C
�C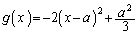
(1) 2�̕�����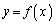 ��
��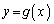 ��2�̋��L�_�����悤��a�͈̔͂����߂�B
��2�̋��L�_�����悤��a�͈̔͂����߂�B (2) (1)�ŋ��߂��͈͂ɑ�����a�̒l�ɑ��āA2�̕������ɂ���Ĉ͂܂��}�`��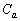 �Ƃ���B
�Ƃ���B �̖ʐς�a�ŕ\���B
�̖ʐς�a�ŕ\���B (3) a��(1)�ŋ��߂��͈͂��Ƃ��A���Ȃ��Ƃ�1��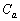 �ɑ�����_�S�̂���Ȃ�}�`�̖ʐς����߂�B
�ɑ�����_�S�̂���Ȃ�}�`�̖ʐς����߂�B
���@��Ԃ̕p�o���ł��B(3)��x���Œ肵a�̊��Ƃ݂čő�l���l���A�̈�����߂܂��B
(1) 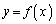 ��
��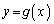 ��A�����āA
��A�����āA ��������ƁA
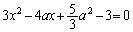 �@����@
�@����@2�̕�����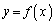 ��
��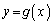 ��2�̋��L�_�����Ƃ��A2���������@�́A���قȂ�2�������������A���ʎ�D�́A
��2�̋��L�_�����Ƃ��A2���������@�́A���قȂ�2�������������A���ʎ�D�́A 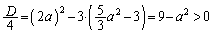 �@����A
�@����A�� 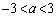 ......[��]
......[��]
(2) 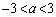 �ł���Ƃ��ɁA�@��2����α�Cβ (
�ł���Ƃ��ɁA�@��2����α�Cβ (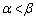 )�Ƃ��āA
)�Ƃ��āA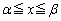 �ɂ����Ă�
�ɂ����Ă�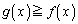 ���A
���A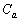 ���ʐ��́A
���ʐ��́A 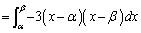 �@(
�@(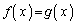 ��2����α�Cβ �ł��邱�Ƃɒ���)
��2����α�Cβ �ł��邱�Ƃɒ���)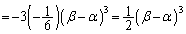 �@����B�@(��ϕ��̌������Q��)
�@����B�@(��ϕ��̌������Q��)�Ƃ���ŁA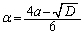 �C
�C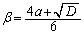 �ƇA���A
�ƇA���A �B�ɑ�����āA
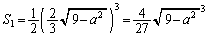 ......[��]
......[��]
(3) 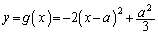 �̃O���t�́Aa�������Ƃ���������������čl���ɂ����̂ŁA����x���W�̂Ƃ���ł����l���邱�Ƃɂ��܂��B����x���W�̂Ƃ���ł́Aa���ς��ƃO���t�������̂ɔ����Ay���W���ω����܂��B����y���W�̂Ƃ蓾��͈͂��A�u���Ȃ��Ƃ�1��
�̃O���t�́Aa�������Ƃ���������������čl���ɂ����̂ŁA����x���W�̂Ƃ���ł����l���邱�Ƃɂ��܂��B����x���W�̂Ƃ���ł́Aa���ς��ƃO���t�������̂ɔ����Ay���W���ω����܂��B����y���W�̂Ƃ蓾��͈͂��A�u���Ȃ��Ƃ�1��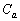 �ɑ�����_�S�̂���Ȃ�v�}�`K������x���W�̂Ƃ���Őؒf�����Ƃ���y���W�͈̔͂ɂȂ�܂��B
�ɑ�����_�S�̂���Ȃ�v�}�`K������x���W�̂Ƃ���Őؒf�����Ƃ���y���W�͈̔͂ɂȂ�܂��B �����ŁAx���Œ肵��a�������Ƃ���y�͈̔͂��l���邱�Ƃɂ��܂�(2�����̍ő�ŏ����Q��)�B y�̍ő�l�ɂ��ẮA���ʒu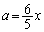 ���A�͈�
���A�͈�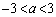 �̉E���ɂ���̂�(
�̉E���ɂ���̂�(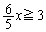 �C�܂�
�C�܂�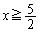 )�A�܂܂��̂�(
)�A�܂܂��̂�(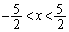 )�A�����ɂ���̂�(
)�A�����ɂ���̂�(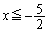 )�ŏꍇ�������Ay�̍ŏ��l�ɂ��ẮA���ʒu���͈�
)�ŏꍇ�������Ay�̍ŏ��l�ɂ��ẮA���ʒu���͈�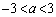 �̒��Ԉʒu
�̒��Ԉʒu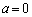 �̍�����(
�̍�����(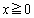 )�E����(
)�E����(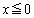 )�ŏꍇ�������čl���邱�Ƃɂ��܂��B
)�ŏꍇ�������čl���邱�Ƃɂ��܂��B
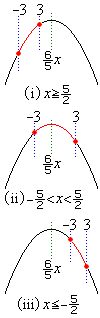 (i)
(i) 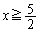 �̂Ƃ��A���ʒu�͔͈�
�̂Ƃ��A���ʒu�͔͈�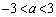 �̉E���ɗ��܂��B�E�}���Ay�̍ő�l�́A
�̉E���ɗ��܂��B�E�}���Ay�̍ő�l�́A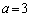 �̂Ƃ��A
�̂Ƃ��A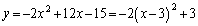
(ii) 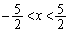 �̂Ƃ��A���ʒu�͔͈�
�̂Ƃ��A���ʒu�͔͈�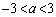 �̒��ɂ���܂��B�E�}���Ay�̍ő�l�́A
�̒��ɂ���܂��B�E�}���Ay�̍ő�l�́A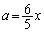 �̂Ƃ��A
�̂Ƃ��A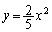
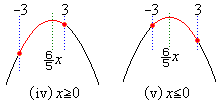 (iv)
(iv) 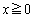 �̂Ƃ��A���ʒu�͔͈�
�̂Ƃ��A���ʒu�͔͈�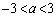 �̒��Ԉʒu�����E�ɗ��܂��B�E�}���Ay�̍ŏ��l�́A
�̒��Ԉʒu�����E�ɗ��܂��B�E�}���Ay�̍ŏ��l�́A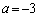 �̂Ƃ��A
�̂Ƃ��A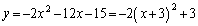
(v) 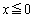 �̂Ƃ��A���ʒu�͔͈�
�̂Ƃ��A���ʒu�͔͈�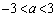 �̒��Ԉʒu�������ɗ��܂��B�E�}���Ay�̍ŏ��l�́A
�̒��Ԉʒu�������ɗ��܂��B�E�}���Ay�̍ŏ��l�́A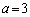 �̂Ƃ��A
�̂Ƃ��A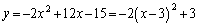
���E����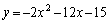 �@����C�@�ƁA
�@����C�@�ƁA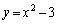 �@����D�@��A������ƁA
�@����D�@��A������ƁA �� 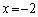 �C�ƇD��
�C�ƇD��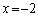 �ɂ����Đڂ��܂��B
�ɂ����Đڂ��܂��B
���E����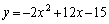 �@����E�@�ƁA�D��A������ƁA
�@����E�@�ƁA�D��A������ƁA �E�ƇD��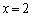 �ɂ����Đڂ��܂��B
�ɂ����Đڂ��܂��B
���E����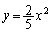 �@����F�@�ƁA�D��A������ƁA
�@����F�@�ƁA�D��A������ƁA �� 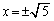 �F�ƇD��
�F�ƇD��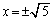 �ɂ����Č����܂��B
�ɂ����Č����܂��B
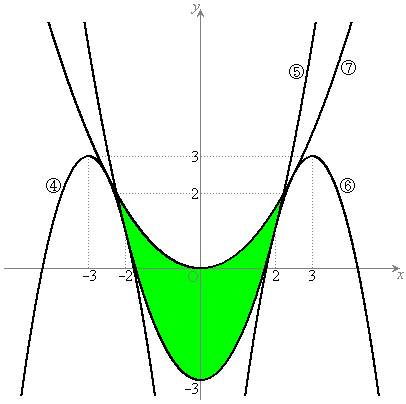 �ȏ���A�}�`K�́A
�ȏ���A�}�`K�́A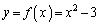 ����㑤��
����㑤��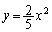 ���牺���̕����ɂȂ�܂�(�E�}���ΐF���F����)�B���̖ʐ�
���牺���̕����ɂȂ�܂�(�E�}���ΐF���F����)�B���̖ʐ�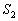 �́A
�́A 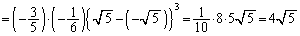 ......[��]
......[��]
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���w��b����TOP�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B