�ꋴ�吔�w'07�N�O��[1]
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
m�𐮐��Ƃ��A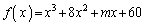 �Ƃ���B
�Ƃ���B
(1) ����a�ƁA0�ł͂Ȃ�����b�ŁA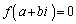 ���݂������̂����݂���悤��m�����ׂċ��߂�B�������Ai�͋����P�ʂł���B
���݂������̂����݂���悤��m�����ׂċ��߂�B�������Ai�͋����P�ʂł���B (2) (1)�ŋ��߂����ׂĂ�m�ɑ��āA������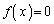 �������B
�������B
���@
(1) 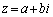 �Ƃ����ƁA
�Ƃ����ƁA ����āA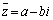 ��
��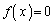 �̉��ł��B
�̉��ł��B
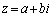 �C
�C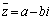 ��2���Ƃ���2�������������߂܂��B
��2���Ƃ���2�������������߂܂��B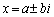 �C
�C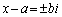 ��2�悷��ƁA
��2�悷��ƁA ���ꂪ�Az�C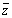 ��2���Ƃ���2���������ł��B
��2���Ƃ���2���������ł��B
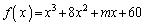 ��
��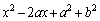 �Ŋ���Ɗ�����͂��ł����A����
�Ŋ���Ɗ�����͂��ł����A����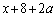 �C�]��ɂ��āA
�C�]��ɂ��āA ����āA
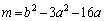 �@����@
�@����@
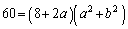 �@����A
�@����A�A���A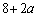 ��
��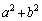 ��60�̖�(�������Q��)�ŁA
��60�̖�(�������Q��)�ŁA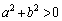 ���
���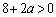
�� 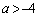 �����������a�ł����āA
�����������a�ł����āA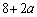 (�����ł�)��60�̖ƂȂ���̂�T���܂��B
(�����ł�)��60�̖ƂȂ���̂�T���܂��B b�������ɂȂ炸�s�K�B
b�������ɂȂ炸�s�K�B
�� 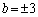 �@���A
�@���A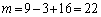 �@����C
�@����C b�������ɂȂ炸�s�K�B
�� 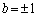 �@���A
�@���A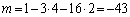 �@����D
�@����D 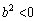 �ƂȂ�s�K�B
�ƂȂ�s�K�B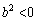 �ƂȂ�s�K�B
�ƂȂ�s�K�B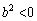 �ƂȂ�s�K�B
�ƂȂ�s�K�B�E����ȊO��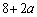 ��60�̖ƂȂ�ꍇ�͂���܂���B
��60�̖ƂȂ�ꍇ�͂���܂���B
�C�C�D���A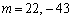 ......[��]
......[��]
(2) �E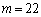 �̂Ƃ��A�C���A
�̂Ƃ��A�C���A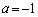 �C
�C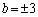 �C�������́A
�C�������́A 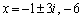 ......[��]
......[��]�E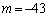 �̂Ƃ��A�D���A
�̂Ƃ��A�D���A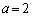 �C
�C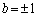 �C�������́A
�C�������́A 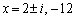 ......[��]
......[��]
[�ʉ�]�@3���������̉��ƌW���̊W�𗘗p���邱�Ƃ��ł��܂��B
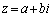 �C
�C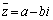 �ȊO�̉���c�Ƃ��āA3���������̉��ƌW���̊W���A
�ȊO�̉���c�Ƃ��āA3���������̉��ƌW���̊W���A
�E���A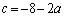
�F�C�G�ɑ�����āA
�ƂȂ�A�@�C�A���o�Ă��܂��B
�ȍ~�́A��L�Ɠ����悤�ɂ���悢�̂ł����A(2)�ł́A�������������Ȃ��Ă��A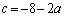 ���炷����3�߂̉��������܂��B
���炷����3�߂̉��������܂��B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���w��b����TOP�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B