�ꋴ�吔�w'09�N�O��[2]
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
(1) �C�ӂ̊pθ �ɑ��āA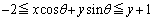 ����������悤�ȓ_
����������悤�ȓ_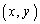 �̑S�̂���Ȃ�̈��xu���ʏ�ɐ}�����A���̖ʐς����߂�B
�̑S�̂���Ȃ�̈��xu���ʏ�ɐ}�����A���̖ʐς����߂�B (2) �C�ӂ̊pα�Cβ �ɑ��āA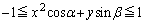 ����������悤�ȓ_
����������悤�ȓ_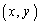 �̑S�̂���Ȃ�̈��xy���ʏ�ɐ}�����A���̖ʐς����߂�B
�̑S�̂���Ȃ�̈��xy���ʏ�ɐ}�����A���̖ʐς����߂�B
���@���T�C�g�̉�����ƁA(1)�ł�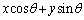 �̍ő�l��
�̍ő�l��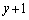 �ȉ��ōŏ��l��
�ȉ��ōŏ��l��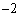 �ȏ�ł���悢�A(2)�ł�
�ȏ�ł���悢�A(2)�ł�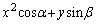 �̍ő�l��1�ȉ��ōŏ��l��
�̍ő�l��1�ȉ��ōŏ��l��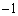 �ȏ�ł���悢�A�ƁA�P���ɏ�����Ă��܂��B�����Ă݂�Ίm���ɂ����Ȃ̂ł����A�_
�ȏ�ł���悢�A�ƁA�P���ɏ�����Ă��܂��B�����Ă݂�Ίm���ɂ����Ȃ̂ł����A�_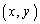 �̑��ݗ̈����ɂ��Ă���̂ŁA�ǂ����Ă�x�Cy�̕��ɖڂ������Ă��܂������ŁA�������ł������z���邱�Ǝ��̂�������낤�Ǝv���܂��B
�̑��ݗ̈����ɂ��Ă���̂ŁA�ǂ����Ă�x�Cy�̕��ɖڂ������Ă��܂������ŁA�������ł������z���邱�Ǝ��̂�������낤�Ǝv���܂��B
���ďo�肳�ꂽ'97�N���[5]�Ȃǂ̓��ł������Ȃ̂ł����A�p�����[�^a���܂�x�Cy�̎��������āA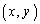 �̑��ݗ̈�����߂�A�Ƃ��A�Ȑ��̒ʉߗ̈�����߂�
�̑��ݗ̈�����߂�A�Ƃ��A�Ȑ��̒ʉߗ̈�����߂� ����ꂽ��Ax�Cy�ł͂Ȃ��A�p�����[�^a�̕��ɒ��ڂ���A�Ƃ������Ƃ��o���Ă����Ă��������B
����ꂽ��Ax�Cy�ł͂Ȃ��A�p�����[�^a�̕��ɒ��ڂ���A�Ƃ������Ƃ��o���Ă����Ă��������B
�{��ł́A(1)�ł�θ �ɁA(2)�ł́A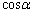 �C
�C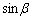 �̕��ɒ��ڂ��܂��B
�̕��ɒ��ڂ��܂��B
(1) 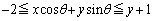 �@����@
�@����@ �E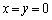 �̂Ƃ��A�@�͔C�ӂ̊pθ �ɑ��Đ�������̂ŁA
�̂Ƃ��A�@�͔C�ӂ̊pθ �ɑ��Đ�������̂ŁA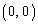 �͋��߂�̈���̓_�ł��B
�͋��߂�̈���̓_�ł��B �E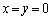 �ł͂Ȃ��Ƃ��A
�ł͂Ȃ��Ƃ��A �������Aδ �́A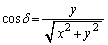 �C
�C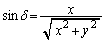 ���݂����p�Bθ ���C�ӂ̊p�ł���Ƃ��A
���݂����p�Bθ ���C�ӂ̊p�ł���Ƃ��A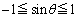
����āA�C�ӂ̊pθ �ɑ��ć@���������邽�߂ɂ́A
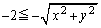 �@����A
�@����A����
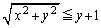 �@����B
�@����B�ł��邱�Ƃ��K�v�\���ł��B
�A���A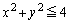 �@����C
�@����C
�B���A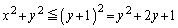
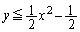 �@����D
�@����D�C�C�D�̋��E���A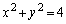 �C
�C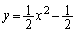 �́A�A������ƁA
�́A�A������ƁA 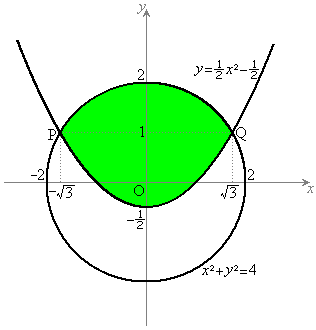
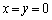 �́A�C�C�D���݂����܂��B
�́A�C�C�D���݂����܂��B
����āA���߂�̈�́A�C���D�ŁA�}������ƉE�}���ΐF���F����(���E�����܂�)�B
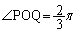 �Ȃ̂ŁA�̈�̖ʐ�
�Ȃ̂ŁA�̈�̖ʐ�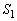 �́A���a2�̉~�̖ʐς�
�́A���a2�̉~�̖ʐς�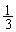 ����A���p
����A���p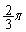 ���͂���2�ӂ̒�����2�̓ӎO�p�`�̖ʐς������āA����
���͂���2�ӂ̒�����2�̓ӎO�p�`�̖ʐς������āA����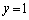 �ƕ�����
�ƕ�����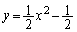 �Ƃň͂܂�镔���̖ʐς����������̂ɂȂ�܂��B
�Ƃň͂܂�镔���̖ʐς����������̂ɂȂ�܂��B
(2) 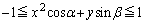 �@����E
�@����E �E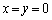 �̂Ƃ��A�E�͔C�ӂ̊pα�Cβ �ɑ��Đ�������̂ŁA
�̂Ƃ��A�E�͔C�ӂ̊pα�Cβ �ɑ��Đ�������̂ŁA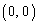 �͋��߂�̈���̓_�ł��B
�͋��߂�̈���̓_�ł��B �E �ł͂Ȃ��Ƃ��A
�ł͂Ȃ��Ƃ��A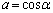 �C
�C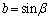 �Ƃ����ƁAα�Cβ ���C�ӂ̊p�ł���A
�Ƃ����ƁAα�Cβ ���C�ӂ̊p�ł���A 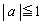 �C
�C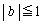 �@����F
�@����F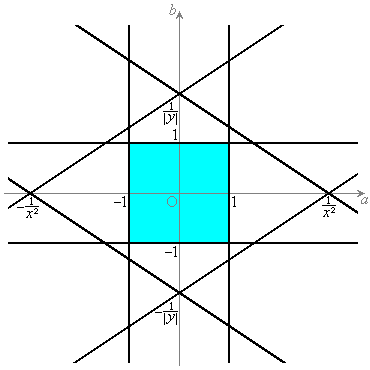 �F���݂����悤��a�Cb�����Ƃ��A
�F���݂����悤��a�Cb�����Ƃ��A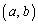 �͉E�}�̐����`�̐��F���F����(���E�����܂�)�ɂ���܂��B
�͉E�}�̐����`�̐��F���F����(���E�����܂�)�ɂ���܂��B�́A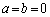 �̂Ƃ��ɂ݂������̂ŁAab���ʂŒ���
�̂Ƃ��ɂ݂������̂ŁAab���ʂŒ���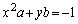 ���猴�_���̗̈��\���܂��B
���猴�_���̗̈��\���܂��B
����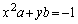 �́Aa�ؕ�
�́Aa�ؕ�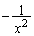 (
(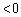 )�Cb�ؕ�
)�Cb�ؕ�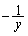 ��a���̕�����ʉ߂��钼���ł�(
��a���̕�����ʉ߂��钼���ł�(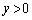 �Ȃ�b���̕����A
�Ȃ�b���̕����A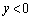 �Ȃ�b���̐�����ʉ߂��܂�)�B
�Ȃ�b���̐�����ʉ߂��܂�)�B �́A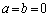 �̂Ƃ��ɂ݂������̂ŁAab���ʂŒ���
�̂Ƃ��ɂ݂������̂ŁAab���ʂŒ���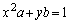 ���猴�_���̗̈��\���܂��B
���猴�_���̗̈��\���܂��B
����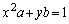 �́Aa�ؕ�
�́Aa�ؕ�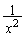 (
(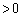 )�Cb�ؕ�
)�Cb�ؕ�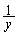 ��a���̐�����ʉ߂��钼���ł�(
��a���̐�����ʉ߂��钼���ł�(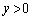 �Ȃ�b���̐����A
�Ȃ�b���̐����A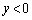 �Ȃ�b���̕�����ʉ߂��܂�)�B
�Ȃ�b���̕�����ʉ߂��܂�)�B
�]���āA�F���݂����C�ӂ�a�Cb���E���݂������߂ɂ́A�E�}�̐����`�̒��_�A �ɂ����ćE���݂�����邱�Ƃ��K�v�\���ł��B����āA
�����A
�����ŁA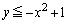 �ł����
�ł����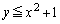 �݂͂�����A
�݂͂�����A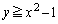 �ł����
�ł����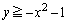 �݂͂������̂ŁA
�݂͂������̂ŁA 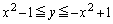 �@����G
�@����G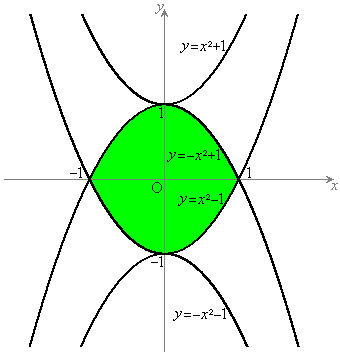
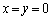 �͇E���݂����܂��B
�͇E���݂����܂��B
����āA���߂�̈�͇G�ŁA�}������ƉE�}���ΐF���F����(���E�����܂�)�B
�̈�̖ʐ�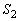 �́Ax���ƕ�����
�́Ax���ƕ�����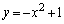 �ň͂܂�镔���̖ʐς�2�{�ŁA
�ň͂܂�镔���̖ʐς�2�{�ŁA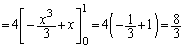 ......[��]
......[��]
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���w��b����TOP�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B