�ꋴ�吔�w'09�N�O��[3]
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
p�Cq�������Ƃ���B������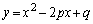 ���A���S
���A���S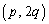 �Ŕ��a1�̉~�ƒ��S
�Ŕ��a1�̉~�ƒ��S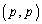 �Ŕ��a1�̉~�̗����Ƌ��L�_�����B���̕������̒��_�����݂�����̈��xy���ʏ�ɐ}������B
�Ŕ��a1�̉~�̗����Ƌ��L�_�����B���̕������̒��_�����݂�����̈��xy���ʏ�ɐ}������B
���@�����Ď��g�݂₷�����Ƃ͌����܂��A'09�N�O���̈ꋴ��̖��̒��ł́A[1]��[3]�����W���I��@�ʼn�������͂Ȃ��̂ŁA���Ƃ����̂ɂ�����1��ł��B
�������F
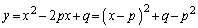 �@����@
�@����@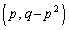 �ɂ���������ł�(2�������Q��)�B
�ɂ���������ł�(2�������Q��)�B
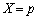 �C
�C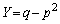
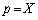 �C
�C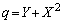 �@����A
�@����A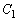 �F
�F
�����L�_�����̂ŁA�������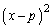 ����������ƁA
����������ƁA
�������āA
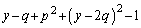 �@����B
�@����B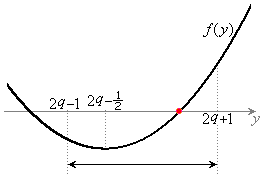 ���̍��ӂ�
���̍��ӂ�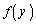 �Ƃ����܂��B�~
�Ƃ����܂��B�~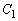 �̑��ݔ͈͂��l����ƁA������
�̑��ݔ͈͂��l����ƁA������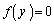 �́A
�́A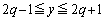 �͈̔͂ɏ��Ȃ��Ƃ�1�������������܂��B
�͈̔͂ɏ��Ȃ��Ƃ�1�������������܂��B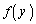 �̎��̈ʒu��
�̎��̈ʒu��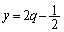 �ʼn��͈̔͂̒��ɂ���̂ŁA���̏���(2���������̉��̔z�u���Q��)�́A
�ʼn��͈̔͂̒��ɂ���̂ŁA���̏���(2���������̉��̔z�u���Q��)�́A
�ł�(�E�}�Q��)�B
���D�~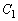 �̑��ݔ͈͂��l�����Ȃ��ƁA
�̑��ݔ͈͂��l�����Ȃ��ƁA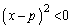 �ƂȂ�悤��y�̎����������蓾�Ă��܂��܂��B
�ƂȂ�悤��y�̎����������蓾�Ă��܂��܂��B
�C���A
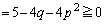 �@����E
�@����E
�� 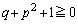 �@����F
�@����F
�܂��A�@�Ɖ~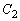 �F
�F
�����L�_�����̂ŁA�������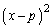 ����������ƁA
����������ƁA
�������āA
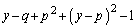 �@����G
�@����G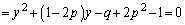 �@����H
�@����H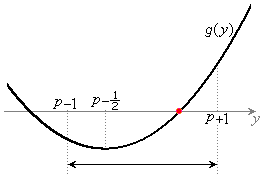 ���̍��ӂ�
���̍��ӂ�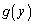 �Ƃ����܂��B�~
�Ƃ����܂��B�~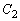 �̑��ݔ͈͂��l����ƁA������
�̑��ݔ͈͂��l����ƁA������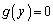 �́A
�́A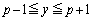 �͈̔͂ɏ��Ȃ��Ƃ�1�������������܂��B
�͈̔͂ɏ��Ȃ��Ƃ�1�������������܂��B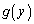 �̎��̈ʒu��
�̎��̈ʒu��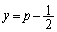 �ʼn��͈̔͂̒��ɂ���̂ŁA���̏����́A
�ʼn��͈̔͂̒��ɂ���̂ŁA���̏����́A
�ł�(�E�}�Q��)�B�I���A
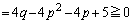 �@����K
�@����K
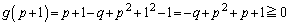 �@����L
�@����L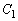 �C
�C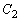 �̗����Ƌ��L�_���������́A�E���F���K���L�ł����A�@�̒��_�̑��ݔ͈͇͂A��p���āA
�̗����Ƌ��L�_���������́A�E���F���K���L�ł����A�@�̒��_�̑��ݔ͈͇͂A��p���āA
�E�́A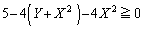
�� 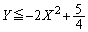
�F�́A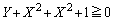
�� 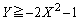
�K�́A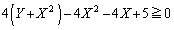
�� 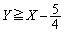
�L�́A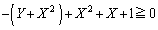
�� 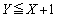
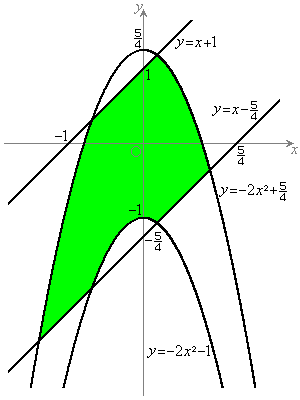 �ȏ���A�@�̒��_�̑��ݔ͈͂́A��L��
�ȏ���A�@�̒��_�̑��ݔ͈͂́A��L��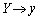 �C
�C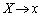 �Ƃ��āA
�Ƃ��āA
�ł����āA�}������ƉE�}���ΐF���F����(���E�����܂�)�B
�Ȃ��A���E��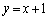 ��
��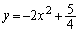 �́A
�́A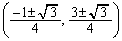 (��������)�ɂ����āA
(��������)�ɂ����āA
���E��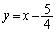 ��
��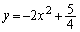 �́A
�́A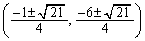 (��������)�ɂ����āA
(��������)�ɂ����āA
���E��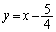 ��
��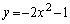 �́A
�́A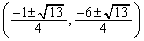 (��������)�ɂ����āA
(��������)�ɂ����āA
�����܂��B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���w��b����TOP�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B