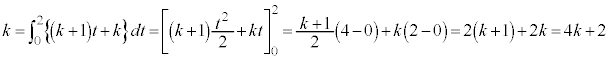積分方程式 関連問題
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
関係式の中に、積分を含むものを積分方程式といいます。
例1.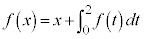 を満たす
を満たす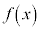 を求める。
を求める。
[解答] 定積分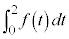 は定数になるので、
は定数になるので、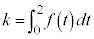 ・・・① とおきます。すると、
・・・① とおきます。すると、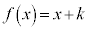 と書けます。この
と書けます。この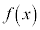 を①に代入して積分すると(定積分を参照)、
を①に代入して積分すると(定積分を参照)、 ∴ 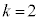 ,
,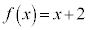 ......[答]
......[答]
例2.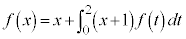 を満たす
を満たす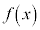 を求める。
を求める。
[解答] 定積分は変数t について行うので、被積分関数内の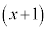 は積分計算する間は定数であって、積分の外に出すことができます。
は積分計算する間は定数であって、積分の外に出すことができます。 例1と同様に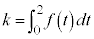 ・・・① とおくと、
・・・① とおくと、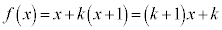 と書けます。この
と書けます。この を①に代入すると、
を①に代入すると、 ∴  ,
,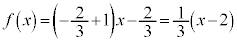 ......[答]
......[答]
例3.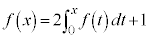 を満たす
を満たす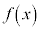 を求める。
を求める。
[解答] 定積分の上端、下端にxを含む場合は、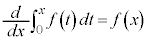 (定積分と微分を参照)を利用し、与式両辺を微分します。
(定積分と微分を参照)を利用し、与式両辺を微分します。
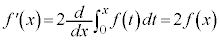 ・・・②
・・・②また、与式の定積分を0とする操作を行います。積分の上端と下端を一致させます。与式では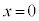 を代入します。
を代入します。 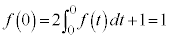 ・・・③
・・・③②より、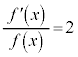 ,両辺を積分する(不定積分の公式を参照)と、
,両辺を積分する(不定積分の公式を参照)と、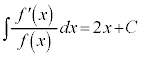 (C:積分定数)
(C:積分定数) 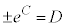 とおくと、
とおくと、③より、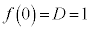
∴ 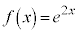 .......[答]
.......[答]
例4.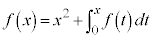 を満たす
を満たす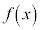 を求める。
を求める。
[解答] 定積分の上端、下端にxを含むので、例3と同様に、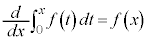 を利用し、与式両辺を微分します。
を利用し、与式両辺を微分します。
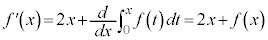 ・・・④
・・・④これは、線形1階微分方程式(微分方程式(その2)を参照)と呼ばれるタイプの微分方程式で、定数変化法を用いて解きます。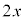 がない場合の方程式
がない場合の方程式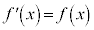 の解は
の解は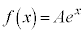 (A:定数)です。
(A:定数)です。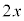 がついた場合の解を、この定数Aが関数
がついた場合の解を、この定数Aが関数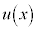 になったものだとして、
になったものだとして、 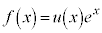 ・・・⑤
・・・⑤とおくと、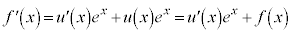
これと④を見比べて、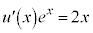 ,つまり、
,つまり、 ,よって、
,よって、 与式で、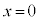 を代入すると、
を代入すると、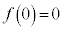 ,⑤より、
,⑤より、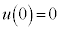 ,よって、
,よって、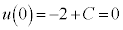 ∴
∴ 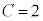 ⑤より、
⑤より、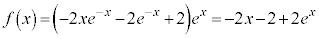 ......[答]
......[答]
例3.例4.のような、積分の上端・下端にxを含むタイプの積分方程式は、微分して微分方程式に直して解くことになります。
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
数学基礎事項TOP 数学TOP TOPページに戻る
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
各問題の著作権は
出題大学に属します。©2005-2024(有)りるらる 苦学楽学塾 随時入会受付中!理系大学受験ネット塾苦学楽学塾(ご案内はこちら)ご入会は、
まず、こちらまでメールを
お送りください。