�c�嗝�H���w'07�N[B1]
(1) 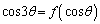 ����3����
����3����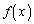 �ƁA
�ƁA ����4����
����4���� �����߂Ȃ����B�܂��A������
�����߂Ȃ����B�܂��A������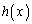 �ŁA
�ŁA �������̂����߂Ȃ����B���ɂ͓��������������ƁB
(2)  ��(1)�ŋ��߂��������Ƃ���B
��(1)�ŋ��߂��������Ƃ���B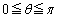 �Ƃ���Ƃ��A
�Ƃ���Ƃ��A �ł��邽�߂ɂ́A
�ł��邽�߂ɂ́A �܂���
�܂���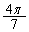 �܂���
�܂���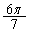 �ł��邱�Ƃ��K�v�\���ł��邱�Ƃ��ؖ����Ȃ����B
�ł��邱�Ƃ��K�v�\���ł��邱�Ƃ��ؖ����Ȃ����B (3)  �̒l�����߂Ȃ����B�l�����łȂ��A�Ȃ������Ȃ�̂����������ƁB
�̒l�����߂Ȃ����B�l�����łȂ��A�Ȃ������Ȃ�̂����������ƁB
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@���R��n�ɑ��āA �ŗ^������n��������
�ŗ^������n��������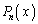 ���`�F�r�V�F�t�̑������ƌ����܂��B
���`�F�r�V�F�t�̑������ƌ����܂��B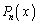 �̒�`��A�l��Ƃ��A
�̒�`��A�l��Ƃ��A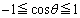 �C
�C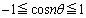 �ƂȂ��Ă��āA
�ƂȂ��Ă��āA �̃O���t��
�̃O���t��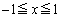 �C
�C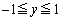 �̐����`�̗̈�ɂ����ۂ�Ǝ��܂�̂Ńn���h�����O���Ղ��A�����ł��悭�̂�グ���܂��B
�̐����`�̗̈�ɂ����ۂ�Ǝ��܂�̂Ńn���h�����O���Ղ��A�����ł��悭�̂�グ���܂��B
(1)  ��3�{�p�̌����ō\��Ȃ��̂ł����A
��3�{�p�̌����ō\��Ȃ��̂ł����A �����߂�̂ŁA
�����߂�̂ŁA �C
�C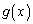 �Ƃ��ɁA2�{�p�̌������g���ċ��߂邱�Ƃɂ��܂��B
�Ƃ��ɁA2�{�p�̌������g���ċ��߂邱�Ƃɂ��܂��B 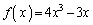 �C
�C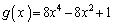 ......[��]
......[��] ��
��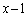 �Ŋ��鏜�Z�����s���邱�Ƃɂ���āA
�Ŋ��鏜�Z�����s���邱�Ƃɂ���āA �@����@
�@����@ ......[��]
......[��]
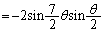 �@����A
�@����A
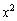 �̌W�����r���邱�Ƃɂ��A
�̌W�����r���邱�Ƃɂ��A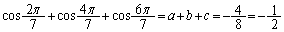 ......[��]
......[��]
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@�c�嗝�H���wTOP�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B