慶大理工数学'07年[A1]
(1) 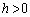 とする。実数aに対して、
とする。実数aに対して、 を考える。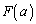 を最小にするようなaを
を最小にするようなaを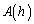 とするとき、
とするとき、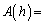 ア ,
ア , イ である。
イ である。
次に、関数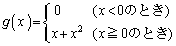 と、実数b,cに対して、
と、実数b,cに対して、 を考える。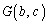 を最小にするようなb,cをそれぞれ
を最小にするようなb,cをそれぞれ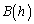 ,
,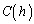 とすれば、
とすれば、 ウ ,
ウ ,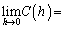 エ である。
エ である。 (2) 正9角形の3つの頂点でできる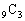 (
(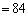 )個の三角形のうち、鈍角三角形の個数は オ 個である。一般に、正整数nに対して、正
)個の三角形のうち、鈍角三角形の個数は オ 個である。一般に、正整数nに対して、正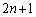 角形の3つの頂点でできる鈍角三角形は、全部で カ 個ある。
角形の3つの頂点でできる鈍角三角形は、全部で カ 個ある。
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
解答(1)(ア) 
これを最小にするaは、
∴  ......[答]
......[答] ∴ 
1 ......[答]
(ウ) 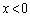 で
で となることに注意して、
となることに注意して、  は、b,cに依存しない定数。
は、b,cに依存しない定数。 ......[答]
......[答](エ) 0 ......[答]
 (2)(オ) 正9角形の頂点に順に、
(2)(オ) 正9角形の頂点に順に、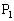 ,
, ,・・・,
,・・・, と名前をつけます。
と名前をつけます。三角形が鈍角三角形になるのは、正9角形の外接円の直径の片側に3頂点がくる場合です。
ここでは、最大辺に目をつけます。
重複して数えないように、最大辺で正9角形を2つに分けるとき、小さい方の多角形に含まれる三角形のみを考えることにします。
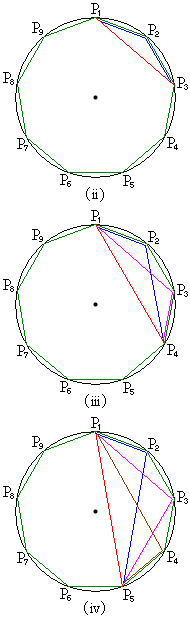
(i) 最大辺の両端が隣接2頂点になることはありません。
(ii) 最大辺の両端が1頂点おいた2頂点、例えば、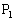 ,
,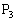 のとき、三角形のもう一つの頂点は
のとき、三角形のもう一つの頂点は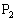 であって、三角形
であって、三角形 は鈍角三角形です。このタイプの鈍角三角形は、最大辺の選び方だけ9個あります。
は鈍角三角形です。このタイプの鈍角三角形は、最大辺の選び方だけ9個あります。 (iii) 最大辺の両端が2頂点おいた2頂点、例えば、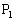 ,
, のとき、三角形のもう一つの頂点は、
のとき、三角形のもう一つの頂点は、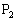 または
または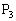 です。三角形
です。三角形 ,三角形
,三角形 は鈍角三角形です。最大辺の選び方が9通りあり、各々について残る頂点の選び方が2通りあるので、このタイプの鈍角三角形は
は鈍角三角形です。最大辺の選び方が9通りあり、各々について残る頂点の選び方が2通りあるので、このタイプの鈍角三角形は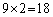 個あります。
個あります。 (iv) 最大辺の両端が3頂点おいた2頂点、例えば、 ,
, のとき、三角形のもう一つの頂点は、
のとき、三角形のもう一つの頂点は、 または
または または
または です。三角形
です。三角形 ,三角形
,三角形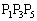 ,三角形
,三角形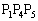 は鈍角三角形です。最大辺の選び方が9通りあり、各々について残る頂点の選び方が3通りあるので、このタイプの鈍角三角形は
は鈍角三角形です。最大辺の選び方が9通りあり、各々について残る頂点の選び方が3通りあるので、このタイプの鈍角三角形は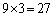 個あります。
個あります。 これですべての場合です。
鈍角三角形は、 個あります。
個あります。 54 ......[答]
(カ) 正 角形の場合(正9角形は
角形の場合(正9角形は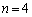 の場合になります)、最大辺の両端の頂点は、1頂点おいた2頂点、から、
の場合になります)、最大辺の両端の頂点は、1頂点おいた2頂点、から、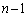 頂点おいた2頂点までの可能性があります。
頂点おいた2頂点までの可能性があります。 正9角形のときと同様に考えて、最大辺で正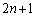 角形を2つに分けるとき、小さい方の多角形に含まれる三角形のみを考えることにします。
角形を2つに分けるとき、小さい方の多角形に含まれる三角形のみを考えることにします。
最大辺がk頂点おいた2頂点となる場合(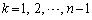 )、このk個の頂点が三角形の残る頂点となる可能性があるのでk通りの三角形ができます。
)、このk個の頂点が三角形の残る頂点となる可能性があるのでk通りの三角形ができます。
いずれのkの値についても、最大辺の選び方は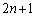 通りあり、鈍角三角形は、
通りあり、鈍角三角形は、 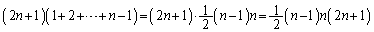 個
個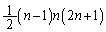 ......[答]
......[答]
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
慶大理工数学TOP 数学TOP TOPページに戻る
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
各問題の著作権は
出題大学に属します。©2005-2024(有)りるらる 苦学楽学塾 随時入会受付中!理系大学受験ネット塾苦学楽学塾(ご案内はこちら)ご入会は、
まず、こちらまでメールを
お送りください。