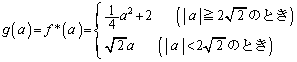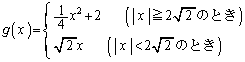�c�嗝�H���w'08�N[A3]
(1) ����a���Œ肵���Ƃ��A����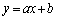 �ƋȐ�
�ƋȐ�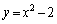 �����L�_�������߂̐ؕ�b�̏�����a��p���Ă���킷��
�����L�_�������߂̐ؕ�b�̏�����a��p���Ă���킷��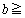 �@�X�@�ł���B
�@�X�@�ł���B (2) ����a���Œ肵���Ƃ��A����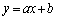 �ƋȐ�
�ƋȐ�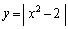 �����L�_�������߂̐ؕ�b�̏����́A
�����L�_�������߂̐ؕ�b�̏����́A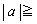 �@�Z�@�̂Ƃ�
�@�Z�@�̂Ƃ�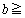 �@�X�@�ł���A
�@�X�@�ł���A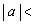 �@�Z�@�̂Ƃ�
�@�Z�@�̂Ƃ�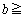 �@�\�@�ƂȂ�B
�@�\�@�ƂȂ�B
���̂悤�ɁAa���Œ肵���Ƃ��A����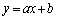 �ƋȐ�
�ƋȐ�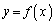 �����L�_�����悤��b�̍ŏ��l�����݂��邱�Ƃ�����B���̍ŏ��l�̕��������������̂�
�����L�_�����悤��b�̍ŏ��l�����݂��邱�Ƃ�����B���̍ŏ��l�̕��������������̂�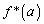 �Ə������Ƃɂ���B���Ƃ���
�Ə������Ƃɂ���B���Ƃ���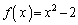 �Ȃ��
�Ȃ��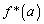 ���|(�@�X�@)�ł���B
���|(�@�X�@)�ł���B
(3) 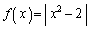 �Ƃ���B
�Ƃ���B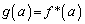 �ƒ�߂āAa��ϐ�x�ŏ�����������
�ƒ�߂āAa��ϐ�x�ŏ�����������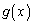 �ɑ���
�ɑ���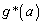 ���l����B
���l����B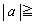 �@�^�@�̂Ƃ�
�@�^�@�̂Ƃ�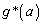 ���@�`�@�ł���A
���@�`�@�ł���A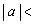 �@�^�@�̂Ƃ�
�@�^�@�̂Ƃ�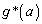 ���@�c�@�ł���B
���@�c�@�ł���B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�� �L���̒�`��^���āA���̋L�����g���čl��������^�C�v�̖��ł����A��̕t���₷����ނŁA�����Ė����łȂ��A�_��Ȏv�l�͂�����ǂ���肾�Ǝv���܂��B
(1)(�X) ����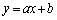 �@����@�@�ƁA�Ȑ�
�@����@�@�ƁA�Ȑ�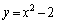 �@����A�@�����L�_�����Ƃ��A�@�C�A��A�����āA
�@����A�@�����L�_�����Ƃ��A�@�C�A��A�����āA 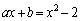
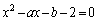 �@����B
�@����B�� 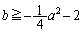 ......[��]�@����C
......[��]�@����C
(2)(�Z) �����@�ƋȐ�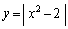 �@����D�@�̋��L�_���l���܂����A�D�́A
�@����D�@�̋��L�_���l���܂����A�D�́A 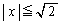 �̂Ƃ��A
�̂Ƃ��A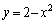
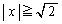 �̂Ƃ��A�A
�̂Ƃ��A�A
�Ȃ̂ŁA(�X)�Ɠ��������ŗǂ��̂́A�B��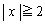 �͈̔͂ɉ������ꍇ�ł��B����́A�B�̍��ӂ�x��2�����ƌ���Ƃ��A���̃O���t�̎��̈ʒu
�͈̔͂ɉ������ꍇ�ł��B����́A�B�̍��ӂ�x��2�����ƌ���Ƃ��A���̃O���t�̎��̈ʒu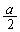 ��
��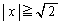 �Ƃ����͈͂ɓ���Ƃ������Ƃł�(2���������̉��̔z�u���Q��)�B�܂�A
�Ƃ����͈͂ɓ���Ƃ������Ƃł�(2���������̉��̔z�u���Q��)�B�܂�A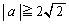 ......[��]
......[��]����́A�����@�̌X���̐�Βl���傫���ꍇ�ɂ́A������y�ؕ�b���C��(�X)�̏��������A�@�ƇD��A������Ƃ��ɁA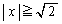 �͈̔͂ɉ��������Ƃ��Ӗ����܂��B
�͈̔͂ɉ��������Ƃ��Ӗ����܂��B 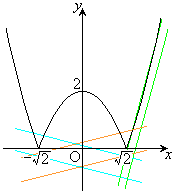
(�\) 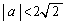 �̂Ƃ��ɂ́A�����@�̌X�����ɂ₩�ŁA�Ȑ��A��
�̂Ƃ��ɂ́A�����@�̌X�����ɂ₩�ŁA�Ȑ��A��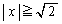 �̕����Ƌ��L�_�������Ȃ����Ƃ����蓾�܂��B
�̕����Ƌ��L�_�������Ȃ����Ƃ����蓾�܂��B �E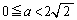 �̂Ƃ��́A�E�}(��F�̐�)���A�����@���_
�̂Ƃ��́A�E�}(��F�̐�)���A�����@���_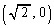 ������ʉ߂���A�����@�ƋȐ��D�����L�_�������܂��B����āA
������ʉ߂���A�����@�ƋȐ��D�����L�_�������܂��B����āA 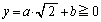 ��
�� 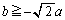 �@����E
�@����E�E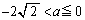 �̂Ƃ��́A�E�}(���F�̐�)���A�����@���_
�̂Ƃ��́A�E�}(���F�̐�)���A�����@���_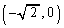 ������ʉ߂���A�����@�ƋȐ��D�����L�_�������܂��B����āA
������ʉ߂���A�����@�ƋȐ��D�����L�_�������܂��B����āA 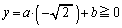 ��
�� 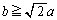 �@����F
�@����F�E�C�F�����킹�āAa�̐����Ɍ��炸�A
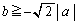 ......[��]
......[��](3)(�^�`) 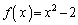 �̂Ƃ��ɁA
�̂Ƃ��ɁA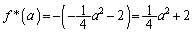 �Ƃ������Ƃ́A
�Ƃ������Ƃ́A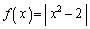 �̂Ƃ��ɂ́A��蕶���A
�̂Ƃ��ɂ́A��蕶���A
�����A
�@��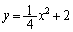 ��A������ƁA
��A������ƁA 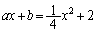
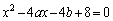 �@����G
�@����G�G�́A���ʎ�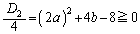 �C�܂�A
�C�܂�A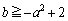 �ł���Ύ������������܂��B
�ł���Ύ������������܂��B
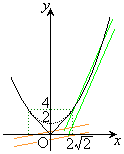
�G�̍��ӂ�x��2�����ƌ���Ƃ��A���̎��̈ʒu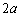 ��
��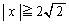 �͈̔͂ɂ���A�܂�A
�͈̔͂ɂ���A�܂�A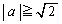 �ł���A�����@��
�ł���A�����@��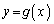 �́A
�́A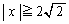 �͈̔͂ɋ��L�_�������܂��B���̂Ƃ��Ab�̍ŏ��l��
�͈̔͂ɋ��L�_�������܂��B���̂Ƃ��Ab�̍ŏ��l��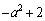 �ł���A
�ł���A ����āA(�^)��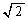 �C(�`)��
�C(�`)��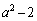 ......[��]
......[��] 
(�c) 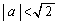 �̂Ƃ��́A�E�}���A�����@�����_
�̂Ƃ��́A�E�}���A�����@�����_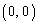 ������ʉ߂���A�����@��
������ʉ߂���A�����@��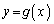 �����L�_�������܂��B����āA
�����L�_�������܂��B����āA �� 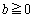 ���̂Ƃ��A
���̂Ƃ��A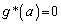 ......[��]
......[��]
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@�c�嗝�H���wTOP�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B