�c�嗝�H���w'13�N[3]
(1) ���W���ʏ�ŁA�_P�����_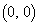 ���o�����Ď���2�̃��[���ɏ]���Ĉړ����J��Ԃ��A���_�����~����܂ňړ������_�����ɐ����Ō���łł�����̂��o�H�Ƃ������Ƃɂ���B
���o�����Ď���2�̃��[���ɏ]���Ĉړ����J��Ԃ��A���_�����~����܂ňړ������_�����ɐ����Ō���łł�����̂��o�H�Ƃ������Ƃɂ���B ���[��1�F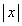 �܂���y��4�ƂȂ�_
�܂���y��4�ƂȂ�_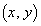 �ɒB����܂ňړ����J��Ԃ��A���̓_�Œ�~����B
�ɒB����܂ňړ����J��Ԃ��A���̓_�Œ�~����B ���[��2�F�_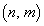 �̎��Ɉړ��ł���̂́A3�_
�̎��Ɉړ��ł���̂́A3�_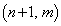 �C
�C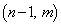 �C
�C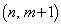 �̂��������ꂩ�̓_�ł���B�������A���_����т���܂łɈړ������_�ɂ͈ړ����Ȃ��B
�̂��������ꂩ�̓_�ł���B�������A���_����т���܂łɈړ������_�ɂ͈ړ����Ȃ��B ���̂Ƃ��A�_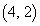 �Œ�~����o�H�͑S����
�Œ�~����o�H�͑S����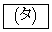 �ʂ�ł���B
�ʂ�ł���B
�܂��A���ׂĂ̌o�H�� �ʂ�ł���A���̂����A�_
�ʂ�ł���A���̂����A�_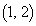 ��ʂ�o�H�͑S����
��ʂ�o�H�͑S����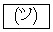 �ʂ�ł���B
�ʂ�ł���B
(2) a�������Ƃ��A��
���l����B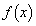 �̍ŏ��l��a�ł���Ƃ���B���̂Ƃ��A
�̍ŏ��l��a�ł���Ƃ���B���̂Ƃ��A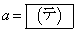 �ł���A
�ł���A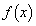 ��
��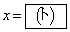 �ōŏ��l�łȂ��ɏ��l
�ōŏ��l�łȂ��ɏ��l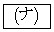 ���Ƃ�B
���Ƃ�B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@(1)�C(2)�͕ʂ̖��ł����A�����Ƃ��A�ׂ����_�o���g���Ē��J�ɏꍇ�������Ē��ׂčs���K�v������܂��B�Ȃ��A�ꍇ�̐��A��Βl�A�����E�s�������Q�Ƃ��Ă��������B
(1) ���[�����A�_P�͏����(y��������)�ɂ͈ړ��ł��܂����������ɂ͈ړ��ł��܂���B
x���ɕ��s�Ȓ�����ł͈�x�E����(x��������)�ɓ����ƍ������ɂ͈ړ��ł��܂���B�܂��A��x�������ɓ����ƉE�����ɂ͈ړ��ł��܂���B
�܂��A�_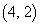 �Œ�~����o�H���l���܂��B
�Œ�~����o�H���l���܂��B
�_P�́A����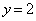 ��ł͉E�Ɉړ����ē_
��ł͉E�Ɉړ����ē_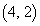 �ɓ��B����̂ŁA����
�ɓ��B����̂ŁA����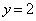 ��ł͉E�Ɉړ����܂��B
��ł͉E�Ɉړ����܂��B
����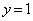 ��Ax����ł͂ǂ���̕����ɂ��ړ��ł��āA
��Ax����ł͂ǂ���̕����ɂ��ړ��ł��āA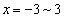 ��7�J���̂����ꂩ�ŏ�����Ɉړ����邱�ƂɂȂ�܂��Bx�����
��7�J���̂����ꂩ�ŏ�����Ɉړ����邱�ƂɂȂ�܂��Bx�����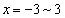 �̂ǂ��ŏ�����Ɉړ����Ă��A����
�̂ǂ��ŏ�����Ɉړ����Ă��A����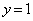 ��ł́A
��ł́A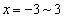 �̂ǂ��ł�������Ɉړ��ł��܂��B
�̂ǂ��ł�������Ɉړ��ł��܂��B
�]���āA�_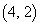 �Œ�~����o�H�͑S����
�Œ�~����o�H�͑S����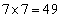 �ʂ肠��܂��B(�^) 49 ......[��]
�ʂ肠��܂��B(�^) 49 ......[��]
(�^)�Ɠ��l�ɂ��āA�_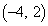 �Œ�~����o�H��49�ʂ肠��܂��B
�Œ�~����o�H��49�ʂ肠��܂��B
�_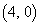 �Œ�~����o�H��1�ʂ�A�_
�Œ�~����o�H��1�ʂ�A�_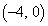 �Œ悷��o�H��1�ʂ�ł��B
�Œ悷��o�H��1�ʂ�ł��B
�_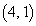 �Œ�~����o�H�́Ax�����
�Œ�~����o�H�́Ax�����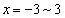 �̂ǂ��ŏ�����Ɉړ����邩7�ʂ�A�_
�̂ǂ��ŏ�����Ɉړ����邩7�ʂ�A�_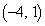 �Œ�~����o�H��7�ʂ�B
�Œ�~����o�H��7�ʂ�B
�_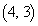 �Œ�~����o�H�́Ax�����
�Œ�~����o�H�́Ax�����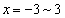 �̂ǂ��ŏ�����Ɉړ����Ă�����
�̂ǂ��ŏ�����Ɉړ����Ă�����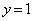 ��ł�
��ł�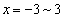 �̂ǂ��ł�������Ɉړ��ł��āA����ɁA����
�̂ǂ��ł�������Ɉړ��ł��āA����ɁA����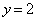 ��ɂ����Ă�
��ɂ����Ă�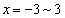 �̂ǂ��ł�������Ɉړ����A����
�̂ǂ��ł�������Ɉړ����A����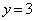 ��ʼnE�����Ɉړ�����Γ_
��ʼnE�����Ɉړ�����Γ_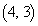 �ɓ��B���܂��B����āA���̌o�H��
�ɓ��B���܂��B����āA���̌o�H��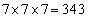 �ʂ肠��܂��B
�ʂ肠��܂��B
�_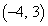 �Œ�~����o�H��343�ʂ肠��܂��B
�Œ�~����o�H��343�ʂ肠��܂��B
����ɁA����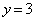 ����ړ�����
����ړ�����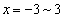 �̂ǂ����ŏ�����Ɉړ�����Β���
�̂ǂ����ŏ�����Ɉړ�����Β���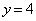 ��ɓ��B���܂����A���̌o�H�̐���
��ɓ��B���܂����A���̌o�H�̐���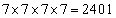 �ʂ肠��܂��B
�ʂ肠��܂��B
�ȏ���A���ׂĂ̌o�H�́A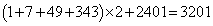 �ʂ肠��܂��B(�`) 3201 ......[��]
�ʂ肠��܂��B(�`) 3201 ......[��]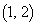 ��ʂ�o�H���l����Ƃ��A
��ʂ�o�H���l����Ƃ��A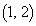 �ɉ����痈��̂��A�E���痈��̂��A�����痈��̂���
�ɉ����痈��̂��A�E���痈��̂��A�����痈��̂���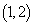 �����̓��������ς��̂ŁA�ꍇ�������čl���܂��B
�����̓��������ς��̂ŁA�ꍇ�������čl���܂��B (i) 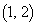 �ɉ����痈��ꍇ�Ax�����
�ɉ����痈��ꍇ�Ax�����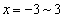 �̂ǂ����ŏ�����Ɉړ����A���̌�
�̂ǂ����ŏ�����Ɉړ����A���̌�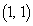 �ŏ�����Ɉړ�����̂ł����A���̌o�H��7�ʂ肠��܂��B
�ŏ�����Ɉړ�����̂ł����A���̌o�H��7�ʂ肠��܂��B 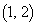 �����́A����
�����́A����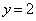 ��ō��E�ɂ��ړ��ł��܂��B
��ō��E�ɂ��ړ��ł��܂��B�E����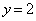 ��ʼnE�Ɉړ��𑱂���Γ_
��ʼnE�Ɉړ��𑱂���Γ_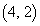 �ɓ��B���A���Ɉړ��𑱂���Γ_
�ɓ��B���A���Ɉړ��𑱂���Γ_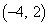 �ɓ��B���܂��B���̌o�H��1�ʂ肸����܂��B
�ɓ��B���܂��B���̌o�H��1�ʂ肸����܂��B �E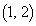 ���獶�E�ɓ�������A���邢�͒��ځA����
���獶�E�ɓ�������A���邢�͒��ځA����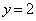 �ォ�������Ɉړ�����̂��A
�ォ�������Ɉړ�����̂��A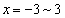 �̂ǂ��ňړ����邩7�ʂ肠��܂��B���̌�A����
�̂ǂ��ňړ����邩7�ʂ肠��܂��B���̌�A����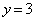 ��ʼnE�Ɉړ��𑱂���Γ_
��ʼnE�Ɉړ��𑱂���Γ_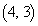 �ɓ��B���A���Ɉړ��𑱂���Γ_
�ɓ��B���A���Ɉړ��𑱂���Γ_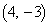 �ɓ��B���܂��B���̌o�H��7�ʂ肸����܂��B
�ɓ��B���܂��B���̌o�H��7�ʂ肸����܂��B �E����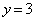 ���
���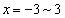 �̂ǂ����ŏ�����Ɉړ�����A����
�̂ǂ����ŏ�����Ɉړ�����A����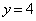 ��ɓ��B���܂��B���̌o�H��
��ɓ��B���܂��B���̌o�H��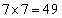 �ʂ肠��܂��B
�ʂ肠��܂��B �ȏ�ŁA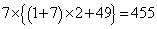 �ʂ�̌o�H������܂��B
�ʂ�̌o�H������܂��B (ii) 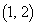 �ɉE���痈��ꍇ�A����
�ɉE���痈��ꍇ�A����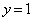 ��ł́A
��ł́A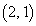 �C
�C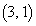 �̂����ꂩ�ŏ�����Ɉړ��������ƂɂȂ�܂��Bx����ł�
�̂����ꂩ�ŏ�����Ɉړ��������ƂɂȂ�܂��Bx����ł�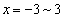 �̂ǂ��ŏ�����Ɉړ����邩7�ʂ肠��̂ŁA
�̂ǂ��ŏ�����Ɉړ����邩7�ʂ肠��̂ŁA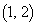 �ɗ���܂ł̌o�H�́A
�ɗ���܂ł̌o�H�́A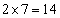 �ʂ肠��܂��B���̌�A
�ʂ肠��܂��B���̌�A �E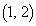 ���獶�Ɉړ���������A
���獶�Ɉړ���������A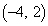 �ɓ��B���܂��B���̌o�H��1�ʂ�B
�ɓ��B���܂��B���̌o�H��1�ʂ�B �E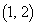 ���獶�ɓ����Ă���A���邢�͒��ځA����
���獶�ɓ����Ă���A���邢�͒��ځA����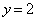 �ォ�������Ɉړ�����̂��A5�ʂ肠��܂��B
�ォ�������Ɉړ�����̂��A5�ʂ肠��܂��B ���̌�A����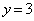 ����E�Ɉړ���������
����E�Ɉړ���������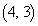 �ɓ��B���邩�A���Ɉړ���������
�ɓ��B���邩�A���Ɉړ���������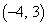 �ɓ��B���邩��2�ʂ肠��܂��B����
�ɓ��B���邩��2�ʂ肠��܂��B����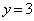 ���
���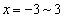 �̂ǂ���7�����ŏ�����Ɉړ�����A����
�̂ǂ���7�����ŏ�����Ɉړ�����A����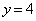 ��ɓ��B���܂��B
��ɓ��B���܂��B �ȏ�ŁA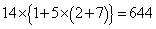 �ʂ�̌o�H������܂��B
�ʂ�̌o�H������܂��B (iii) 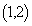 �ɍ����痈��ꍇ�A����
�ɍ����痈��ꍇ�A����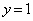 ��ł́A
��ł́A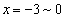 �̂ǂ���4�ʂ�ŏ�����Ɉړ��������ƂɂȂ�܂��Bx����ł�
�̂ǂ���4�ʂ�ŏ�����Ɉړ��������ƂɂȂ�܂��Bx����ł�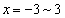 �̂ǂ��ŏ�����Ɉړ����邩7�ʂ肠��̂ŁA
�̂ǂ��ŏ�����Ɉړ����邩7�ʂ肠��̂ŁA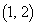 �ɗ���܂ł̌o�H�́A
�ɗ���܂ł̌o�H�́A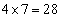 �ʂ肠��܂��B���̌�A
�ʂ肠��܂��B���̌�A �E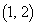 ����E�Ɉړ���������A
����E�Ɉړ���������A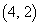 �ɓ��B���܂��B���̌o�H��1�ʂ�B
�ɓ��B���܂��B���̌o�H��1�ʂ�B �E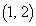 ����E�ɓ����Ă���A���邢�͒��ځA����
����E�ɓ����Ă���A���邢�͒��ځA����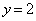 �ォ�������Ɉړ�����̂��A3�ʂ肠��܂��B
�ォ�������Ɉړ�����̂��A3�ʂ肠��܂��B ���̌�A����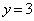 ����E�Ɉړ���������
����E�Ɉړ���������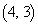 �ɓ��B���邩�A���Ɉړ���������
�ɓ��B���邩�A���Ɉړ���������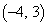 �ɓ��B���邩��2�ʂ肠��܂��B����
�ɓ��B���邩��2�ʂ肠��܂��B����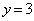 ���
���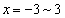 �̂ǂ���7�����ŏ�����Ɉړ�����A����
�̂ǂ���7�����ŏ�����Ɉړ�����A����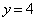 �ɓ��B���܂��B
�ɓ��B���܂��B �ȏ�ŁA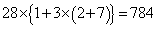 �ʂ�̌o�H������܂��B
�ʂ�̌o�H������܂��B �_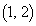 ��ʂ�o�H���S���ŁA
��ʂ�o�H���S���ŁA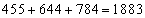 �ʂ�B(�c) 1883 ......[��]
�ʂ�B(�c) 1883 ......[��]
(2) ��Βl�L�����̐����ŏꍇ�������܂��B
(i) 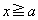 �̂Ƃ��A
�̂Ƃ��A 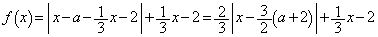 �@����@
�@����@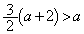 �Ƃ���ƁA
�Ƃ���ƁA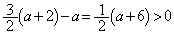 �@��
�@�� 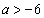
�ȉ��A�܂��A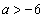 �Ƃ��čl���܂��B
�Ƃ��čl���܂��B�E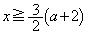 (
(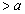 )�̂Ƃ��A
)�̂Ƃ��A ���͈̔͂ɂ�����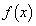 �͑������Ȃ̂ŁA
�͑������Ȃ̂ŁA 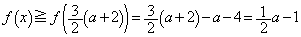 �@����A
�@����A�E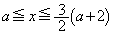 �̂Ƃ��A
�̂Ƃ��A ���͈̔͂ɂ�����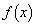 �͌������Ȃ̂ŁA
�͌������Ȃ̂ŁA 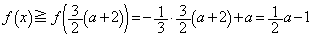 �@����B
�@����B(ii) 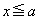 �̂Ƃ��A
�̂Ƃ��A 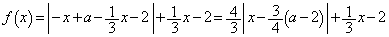 �@����C
�@����C�����ŁA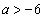 �̏ꍇ���l���Ă���̂ŁA
�̏ꍇ���l���Ă���̂ŁA 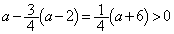 �@��
�@�� 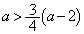
�E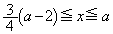 �̂Ƃ��A
�̂Ƃ��A ���͈̔͂ɂ�����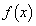 �͑������Ȃ̂ŁA
�͑������Ȃ̂ŁA 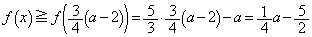 �@����D
�@����D�E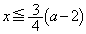 �̂Ƃ��A
�̂Ƃ��A ���͈̔͂ɂ�����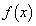 �͌������Ȃ̂ŁA
�͌������Ȃ̂ŁA 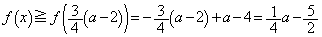 �@����E
�@����E�A�C�B�C�D�C�E���A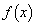 �̍ŏ��l��
�̍ŏ��l��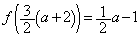 ��
��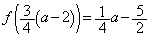 �̂����̏��������ł��B
�̂����̏��������ł��B
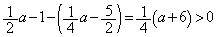 ���A
���A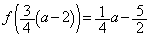 ���ŏ��l�ŁA
���ŏ��l�ŁA ���x�́A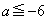 �Ƃ��čl���܂��B���̂Ƃ��́A
�Ƃ��čl���܂��B���̂Ƃ��́A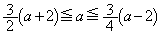 �ƂȂ�A
�ƂȂ�A (i) 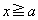 �̂Ƃ��A
�̂Ƃ��A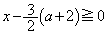 �ł����āA�@���A
�ł����āA�@���A 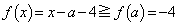 �@����G
�@����G(ii) 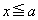 �̂Ƃ��A
�̂Ƃ��A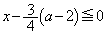 �ł����āA�C���A
�ł����āA�C���A 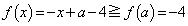 �@����H
�@����H�G�C�H���A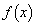 �̍ŏ��l��
�̍ŏ��l��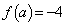 �ł��B���̂Ƃ��A
�ł��B���̂Ƃ��A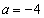 �ƂȂ�܂����A
�ƂȂ�܂����A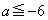 �������s�K�ł��B
�������s�K�ł��B
�F���A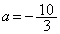 �ł���A
�ł���A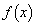 ��
��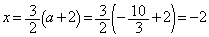 �ōŏ��l�łȂ��ɏ��l
�ōŏ��l�łȂ��ɏ��l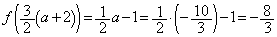 ���Ƃ�B(�e)
���Ƃ�B(�e) 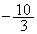 �@(�g)
�@(�g) 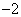 �@(�i)
�@(�i) 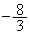 ......[��]
......[��]
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@�c�嗝�H���wTOP�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B