慶大理工数学'22年[5]
半径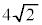 の球面S上に3点A,B,Cがあり、線分AB,BC,CAの長さはそれぞれ
の球面S上に3点A,B,Cがあり、線分AB,BC,CAの長さはそれぞれ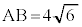 ,
,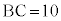 ,
,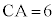 とする。
とする。
(1) 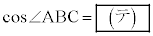 である。平面ABCで球面Sを切った切り口の円をTとする。Tの半径は
である。平面ABCで球面Sを切った切り口の円をTとする。Tの半径は である。点Dが円T上を動くとき、△DABの面積の最大値は
である。点Dが円T上を動くとき、△DABの面積の最大値は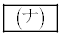 である。
である。
(2) 球面Sの中心Oから平面ABCに下ろした垂線OHの長さは である。
である。
(3) 点Eが球面S上を動くとき、三角錐EABCの体積の最大値は である。
である。
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
解答 円Tは△ABCの外接円なのだということに気付けば、ひっかかるところはないでしょう。
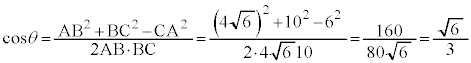 ......[テ]
......[テ]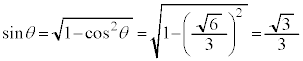
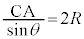 ∴
∴ 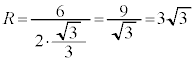 ......[ト]
......[ト]円Tの中心をH,辺ABの中点をQ,円Tと辺ABの垂直二等分線QHとの2交点のうち、中心Hに関して辺ABと逆側にある方をPとして、点Dが円T上を動くとき、△DABの面積が最大になるのは、点Dが点Pに来るときで、
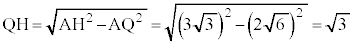 (AHは円Tの半径)
(AHは円Tの半径)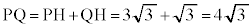
△DABの面積の最大値は、△PABの面積であって、
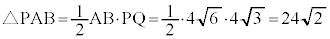 ......[ナ]
......[ナ]
(2) 球面Sの中心Oから平面ABCに垂線を下ろすと、垂線の足は切り口の円Tの中心Hに来ます(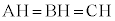 より
より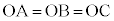 )。△OHAは
)。△OHAは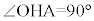 の直角三角形で、
の直角三角形で、 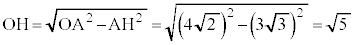 ......[ニ]
......[ニ]
(3) 点Eが球面S上を動くとき、三角錐EABCの体積が最大になるのは、直線OHと球面Sとの2交点のうち、中心Oに関して平面ABCの逆側にある方の交点をUとして、点Eが点Uに来るときです。
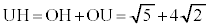 (OUは球面Sの半径)
(OUは球面Sの半径)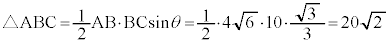
三角錐EABCの体積の最大値は、三角錐UABCの体積であって、
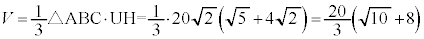 ......[ヌ]
......[ヌ]
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
慶大理工数学TOP 数学TOP TOPページに戻る
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
各問題の著作権は
出題大学に属します。©2005-2024(有)りるらる 苦学楽学塾 随時入会受付中!理系大学受験ネット塾苦学楽学塾(ご案内はこちら)ご入会は、
まず、こちらまでメールを
お送りください。 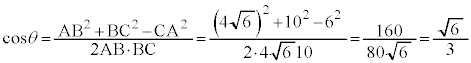 ......[テ]
......[テ]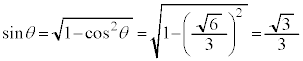
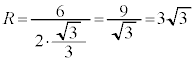 ......[ト]
......[ト]