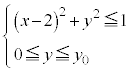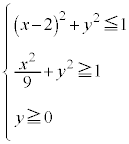慶應大学理工学部2022年数学入試問題
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
[1](1) 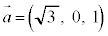 とする。空間のベクトル
とする。空間のベクトル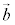 ,
,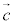 はともに大きさが1であり、
はともに大きさが1であり、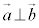 ,
,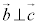 ,
,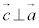 とする。
とする。
(i) p,q,rを実数とし、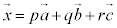 とするとき、内積
とするとき、内積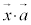 と
と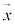 の大きさ
の大きさ をp,q,rを用いて表すと、
をp,q,rを用いて表すと、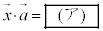 ,
,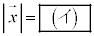 である。
である。
(ii) 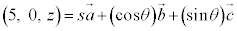 を満たす実数s,θが存在するような実数zは2個あるが、それらをすべて求めると
を満たす実数s,θが存在するような実数zは2個あるが、それらをすべて求めると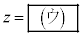 である。
である。
(2) n を奇数とする。nと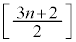 の積が6の倍数であるための必要十分条件は、nを
の積が6の倍数であるための必要十分条件は、nを で割ったときの余りが
で割ったときの余りが となることである。ただし、実数xに対しxを超えない最大の整数を
となることである。ただし、実数xに対しxを超えない最大の整数を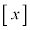 と表す。また、
と表す。また、 ,
,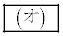 は
は を満たす整数である。
を満たす整数である。 ,
,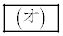 を求める過程を解答欄(2)に記述しなさい。
を求める過程を解答欄(2)に記述しなさい。 [解答へ]
[2] rを正の実数とし、円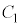 :
: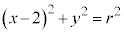 ,楕円
,楕円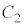 :
: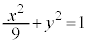 を考える。
を考える。
(1) 円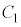 と楕円
と楕円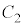 の共有点が存在するようなrの値の範囲は
の共有点が存在するようなrの値の範囲は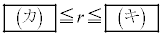 である。
である。
(2) 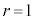 のとき、
のとき、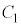 と
と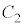 の共有点の座標をすべて求めると
の共有点の座標をすべて求めると である。これらの共有点のうちy座標が正となる点のy座標を
である。これらの共有点のうちy座標が正となる点のy座標を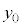 とする。連立不等式
とする。連立不等式 の表す領域の面積は である。
である。
(3) 連立不等式
のあらわす領域をDとする。Dをy軸のまわりに1回転させてできる立体の体積は である。
である。 [解答へ]
[3] 最初に袋の中に白玉が1個入っている。次の規則に従って、1回の操作につき白玉または赤玉を1個ずつ加えていく。
●1回目の操作では、コインを投げ、表が出たときには赤玉を袋の中に1個加え、裏が出たときには白玉を袋の中に1個加える。
●2回目以降の操作では、コインを投げ、表が出たときには赤玉を袋の中に1個加え、裏が出たときには袋から玉を1個無作為に取り出し、その色を見てから袋に戻し、さらに同じ色の玉を袋の中に1個加える。
(1) 2回目の操作を終えたとき、袋の中に白玉がちょうど2個入っている確率は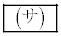 である。
である。
(2) 3回目の操作を終えたとき、コインの表が2回、裏が1回出ていたという条件の下で、袋の中に白玉がちょうど2個入っている条件つき確率は である。
である。
以下、kは2以上の整数とし、k回目の操作を終えたときを考える。。
(3) 袋の中に白玉のみが入っている確率は である。
である。
(4) 1回目の操作で赤玉を加えたという条件の下で、袋の中に白玉がちょうどk個入っている条件つき確率は である。
である。
(5) 袋の中に白玉がちょうどk個入っている確率は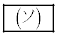 である。
である。 [解答へ]
[4] 曲線C: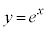 を考える。
を考える。
(1) a,bを実数とし、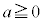 とする。曲線Cと直線
とする。曲線Cと直線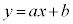 が共有点をもつためのaとbの条件を求め、求める過程とともに解答欄(1)に記述しなさい。
が共有点をもつためのaとbの条件を求め、求める過程とともに解答欄(1)に記述しなさい。
(2) 正の実数t に対し、C上の点A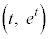 を中心とし、直線
を中心とし、直線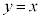 に接する円Dを考える。直線
に接する円Dを考える。直線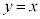 と円Dの接点Bのx座標は
と円Dの接点Bのx座標は であり、円Dの半径は
であり、円Dの半径は である。線分ABを3:2に内分する点をPとし、Pのx座標、y座標をそれぞれ
である。線分ABを3:2に内分する点をPとし、Pのx座標、y座標をそれぞれ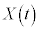 ,
,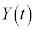 とする。このとき、等式
とする。このとき、等式 が成り立つような実数kを求めると である。ただし、
である。ただし、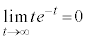 である。
である。 [解答へ]
[5] 半径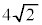 の球面S上に3点A,B,Cがあり、線分AB,BC,CAの長さはそれぞれ
の球面S上に3点A,B,Cがあり、線分AB,BC,CAの長さはそれぞれ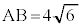 ,
,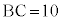 ,
,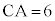 とする。
とする。
(1) 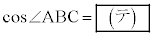 である。平面ABCで球面Sを切った切り口の円をTとする。Tの半径は
である。平面ABCで球面Sを切った切り口の円をTとする。Tの半径は である。点Dが円T上を動くとき、△DABの面積の最大値は
である。点Dが円T上を動くとき、△DABの面積の最大値は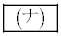 である。
である。
(2) 球面Sの中心Oから平面ABCに下ろした垂線OHの長さは である。
である。
(3) 点Eが球面S上を動くとき、三角錐EABCの体積の最大値は である。
である。 [解答へ]
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
慶大理工数学TOP 数学TOP TOPページに戻る
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
各問題の著作権は
出題大学に属します。©2005-2024(有)りるらる 苦学楽学塾 随時入会受付中!理系大学受験ネット塾苦学楽学塾(ご案内はこちら)ご入会は、
まず、こちらまでメールを
お送りください。