慶大理工数学'22年[4]
曲線C: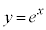 を考える。
を考える。
(1) a,bを実数とし、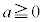 とする。曲線Cと直線
とする。曲線Cと直線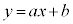 が共有点をもつためのaとbの条件を求め、求める過程とともに解答欄(1)に記述しなさい。
が共有点をもつためのaとbの条件を求め、求める過程とともに解答欄(1)に記述しなさい。
(2) 正の実数t に対し、C上の点A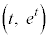 を中心とし、直線
を中心とし、直線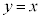 に接する円Dを考える。直線
に接する円Dを考える。直線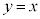 と円Dの接点Bのx座標は
と円Dの接点Bのx座標は であり、円Dの半径は
であり、円Dの半径は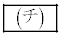 である。線分ABを3:2に内分する点をPとし、Pのx座標、y座標をそれぞれ
である。線分ABを3:2に内分する点をPとし、Pのx座標、y座標をそれぞれ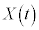 ,
,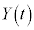 とする。このとき、等式
とする。このとき、等式 が成り立つような実数kを求めると である。ただし、
である。ただし、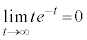 である。
である。
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
解答 想像するに、(2)の極限の出題者の意図は、面倒な計算をしなくても、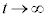 で効いてくるのは
で効いてくるのは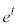 なので、分子
なので、分子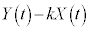 の
の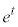 の係数に着目すれば
の係数に着目すれば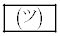 を埋めることができる、ということなんだろうと思います。
を埋めることができる、ということなんだろうと思います。
(1) 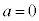 のとき、C:
のとき、C: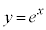 と直線
と直線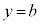 が共有点をもつためには、
が共有点をもつためには、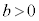 が条件です(指数関数を参照)。
が条件です(指数関数を参照)。 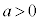 のとき、まず、C:
のとき、まず、C: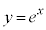 と傾きaの直線
と傾きaの直線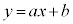 が接する場合を考えてみます。
が接する場合を考えてみます。
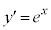 より、
より、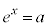 とすると、
とすると、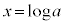 (対数関数を参照)直線
(対数関数を参照)直線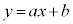 が接点
が接点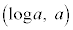 を通るので、
を通るので、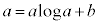 ∴
∴ 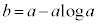
C: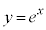 は単調増加で下に凸な曲線なので、曲線C:
は単調増加で下に凸な曲線なので、曲線C: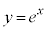 と直線
と直線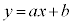 と共有点をもつために、傾きaの直線が傾きaの接線から上側を通ることが必要十分です(微分法の方程式への応用(2)を参照)。つまり、
と共有点をもつために、傾きaの直線が傾きaの接線から上側を通ることが必要十分です(微分法の方程式への応用(2)を参照)。つまり、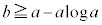
よって求める条件は、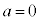 のとき
のとき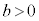 ,
,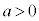 のとき
のとき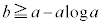 ......[答]
......[答]
(2) 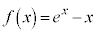 とおくと、
とおくと、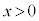 において、
において、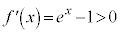 (微分の公式を参照)より、
(微分の公式を参照)より、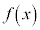 は単調増加なので、
は単調増加なので、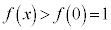 ,つまり
,つまり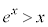 であって、曲線C:
であって、曲線C: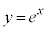 は直線
は直線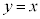 より上にあります。半径ABと接線
より上にあります。半径ABと接線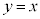 は垂直なので、直線ABの傾きは
は垂直なので、直線ABの傾きは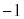 です。直線ABの方程式を、
です。直線ABの方程式を、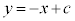 とおくと、点A
とおくと、点A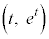 を通るので、
を通るので、 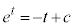 ∴
∴ 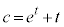
よって、直線AB: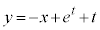
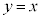 と連立すると、
と連立すると、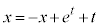 ,交点Bのx座標は、
,交点Bのx座標は、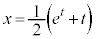 ......[タ]点Bのy座標も
......[タ]点Bのy座標も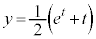 (2直線の交点を参照)円Dの半径は、円の中心A
(2直線の交点を参照)円Dの半径は、円の中心A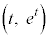 と直線
と直線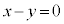 との距離で、
との距離で、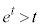 より、
より、 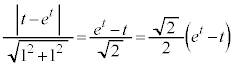 ......[チ]
......[チ]ABを3:2に内分する点P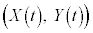 は、
は、
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
慶大理工数学TOP 数学TOP TOPページに戻る
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
各問題の著作権は
出題大学に属します。©2005-2024(有)りるらる 苦学楽学塾 随時入会受付中!理系大学受験ネット塾苦学楽学塾(ご案内はこちら)ご入会は、
まず、こちらまでメールを
お送りください。 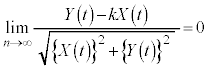
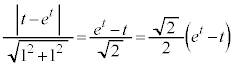 ......[チ]
......[チ]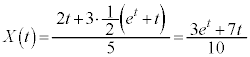 ,
,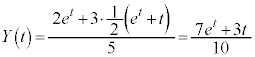
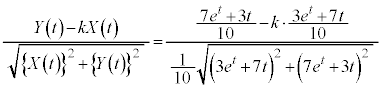
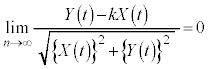 より、
より、