�c�嗝�H���w'22�N[2]
r�𐳂̎����Ƃ��A�~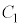 �F
�F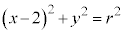 �C�ȉ~
�C�ȉ~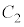 �F
�F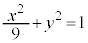 ���l����B
���l����B
(1) �~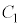 �Ƒȉ~
�Ƒȉ~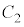 �̋��L�_�����݂���悤��r�̒l�͈̔͂�
�̋��L�_�����݂���悤��r�̒l�͈̔͂�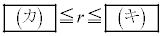 �ł���B
�ł���B
(2) 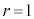 �̂Ƃ��A
�̂Ƃ��A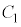 ��
��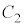 �̋��L�_�̍��W�����ׂċ��߂��
�̋��L�_�̍��W�����ׂċ��߂�� �ł���B�����̋��L�_�̂���y���W�����ƂȂ�_��y���W��
�ł���B�����̋��L�_�̂���y���W�����ƂȂ�_��y���W��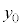 �Ƃ���B�A���s����
�Ƃ���B�A���s���� �̕\���̈�̖ʐς� �ł���B
�ł���B
(3) �A���s����
�̂���킷�̈��D�Ƃ���BD��y���̂܂���1��]�����Ăł��闧�̂̑̐ς� �ł���B
�ł���B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@��^�I�Ȍv�Z���ł��B�ʓ|�Ȃ��ƂɂȂ�Ȃ��悤�ɁA�v�̗̂ǂ��l�����Ői�߂܂��傤�B
(1) 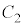 �̎�����A
�̎�����A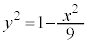 �C
�C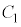 �̎��ɑ������ƁA
�̎��ɑ������ƁA ���ʎ��F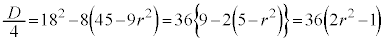 �@����A
�@����A
 ���A
���A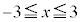
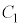 ��
��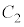 �����L�_�������߂ɁA2���������@��
�����L�_�������߂ɁA2���������@��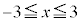 �͈̔͂ɉ������Ă悢(2���������̈�ʘ_���Q��)�킯�ł��B�@���(��)
�͈̔͂ɉ������Ă悢(2���������̈�ʘ_���Q��)�킯�ł��B�@���(��) 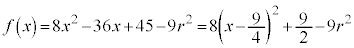 �@����B
�@����B�Ƃ��āA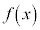 �̎��̈ʒu�ɂ���
�̎��̈ʒu�ɂ���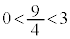 �Ȃ̂ŁA(��)�̂��߂ɁA
�Ȃ̂ŁA(��)�̂��߂ɁA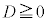 ����
����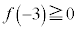 �������ł��B
�������ł��B
����āA�A�C�B���A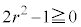 ����
����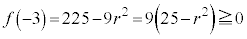
 ���A
���A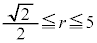 �C
�C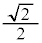 ......[�J]�C5 ......[�L]
......[�J]�C5 ......[�L] �ʉ��D�ȉ~ ��̓_�̍��W
��̓_�̍��W ��θ�������Ƃ���
��θ�������Ƃ���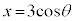 �C
�C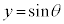 �ƒu�����Ƃ��ł��܂��B�ȉ~��̓_�� �~ �̒��S
�ƒu�����Ƃ��ł��܂��B�ȉ~��̓_�� �~ �̒��S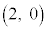 �Ƃ̋�����2��́A
�Ƃ̋�����2��́A 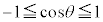 ���A
���A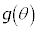 �́A
�́A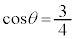 �̂Ƃ��ŏ��l
�̂Ƃ��ŏ��l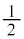 �C
�C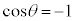 �̂Ƃ��ő�l25���Ƃ�܂�(2�����̍ő�E�ŏ����Q��)�B
�̂Ƃ��ő�l25���Ƃ�܂�(2�����̍ő�E�ŏ����Q��)�B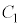 ��
�� �����L�_�������߂ɁA�~�̔��a
�����L�_�������߂ɁA�~�̔��a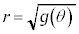 �̒l�͈̔͂́A
�̒l�͈̔͂́A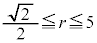
(2) 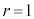 �̂Ƃ��@�́A
�̂Ƃ��@�́A 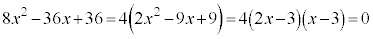 ��
�� 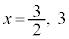
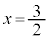 �̂Ƃ��A
�̂Ƃ��A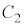 �̎����A
�̎����A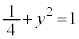 �@��
�@�� 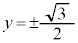
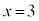 �̂Ƃ��A
�̂Ƃ��A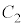 �̎����A
�̎����A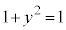 �@��
�@�� 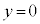
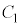 ��
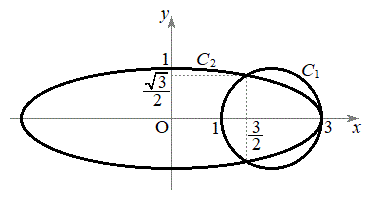
��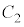 �̋��L�_�́A
�̋��L�_�́A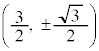 �C
�C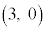 ......[�N]�ʉ��D(1)�̕ʉ��ŁA
......[�N]�ʉ��D(1)�̕ʉ��ŁA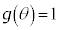 �Ƃ���ƁA
�Ƃ���ƁA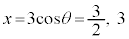 �Ƃ��Ă����߂��܂��B
�Ƃ��Ă����߂��܂��B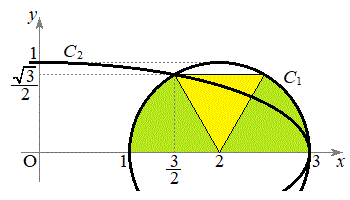
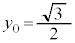 �ł��B�E�}�̂悤�ɁA
�ł��B�E�}�̂悤�ɁA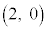 ��
��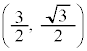 �C
�C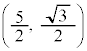 �Ƃ�1�ӂ̒���1�̐��O�p�`���ł���̂ŁA�̈�́A���a1�̉~��
�Ƃ�1�ӂ̒���1�̐��O�p�`���ł���̂ŁA�̈�́A���a1�̉~��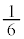 �ƂȂ��`2��(�E�}���ΐF���F��)�ƁA1�ӂ̒���1�̐��O�p�`(�E�}���F���F��)�ɕ����邱�Ƃ��ł��܂��B���̖ʐς́A
�ƂȂ��`2��(�E�}���ΐF���F��)�ƁA1�ӂ̒���1�̐��O�p�`(�E�}���F���F��)�ɕ����邱�Ƃ��ł��܂��B���̖ʐς́A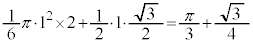 ......[�P]
......[�P]
(3) 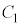 �ɂ��āA
�ɂ��āA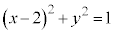 ���A
���A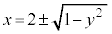 (�����̐��͉~��
(�����̐��͉~��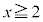 �̕����A�����̕��͉~��
�̕����A�����̕��͉~��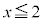 �̕�����\���܂�)
�̕�����\���܂�) 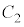 �ɂ��āA
�ɂ��āA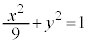 ���A
���A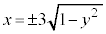 (�ȉ~��
(�ȉ~��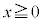 �̕�����\���̂́A���������̏ꍇ�ł�)
�̕�����\���̂́A���������̏ꍇ�ł�)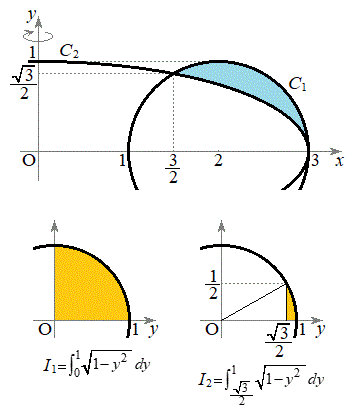 �̈�D�́A�~
�̈�D�́A�~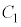 �̓����őȉ~
�̓����őȉ~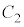 �̊O���ł�����x�������̕����ł�(�E�}���F���F��)�B�̈�D��y���̂܂���1��]������ƁA�~�̉E��
�̊O���ł�����x�������̕����ł�(�E�}���F���F��)�B�̈�D��y���̂܂���1��]������ƁA�~�̉E��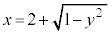 (
(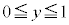 )����]���������̂���A�ȉ~
)����]���������̂���A�ȉ~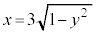 (
(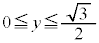 )����]���������̂ƁA�~�̍���
)����]���������̂ƁA�~�̍���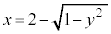 (
(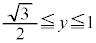 )����]���������̂Ƃ����蔲�������̂ɂȂ�܂��B���߂�̐�V�́A(y���̂܂��̉�]�����Q��)
)����]���������̂Ƃ����蔲�������̂ɂȂ�܂��B���߂�̐�V�́A(y���̂܂��̉�]�����Q��)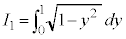 �́A���a1�̉~�̖ʐς�
�́A���a1�̉~�̖ʐς�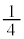 �ŁA
�ŁA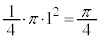 �@(�u���ϕ�(����2)���Q��)
�@(�u���ϕ�(����2)���Q��)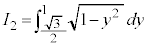 �́A���a1�̉~�̖ʐς�
�́A���a1�̉~�̖ʐς�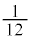 ����A���
����A���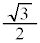 �C����
�C����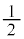 �̎O�p�`�̖ʐς����������̂ŁA
�̎O�p�`�̖ʐς����������̂ŁA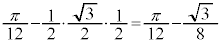
����āA
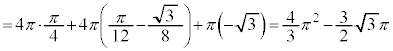 ......[�R]
......[�R]
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@�c�嗝�H���wTOP�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B 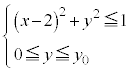
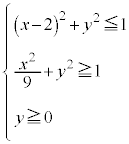
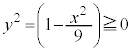 ���A
���A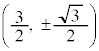 �C
�C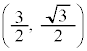 �C
�C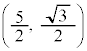 �Ƃ�1�ӂ̒���1�̐��O�p�`���ł���̂ŁA�̈�́A���a1�̉~��
�Ƃ�1�ӂ̒���1�̐��O�p�`���ł���̂ŁA�̈�́A���a1�̉~��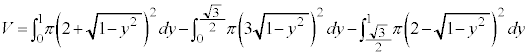
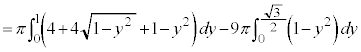
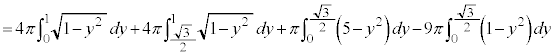
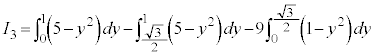
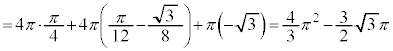 ......[�R]
......[�R]