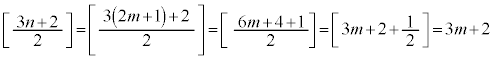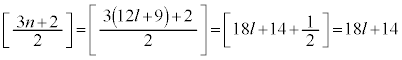慶大理工数学'22年[1]
(1) 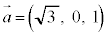 とする。空間のベクトル
とする。空間のベクトル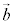 ,
,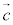 はともに大きさが1であり、
はともに大きさが1であり、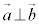 ,
,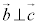 ,
,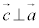 とする。
とする。
(i) p,q,rを実数とし、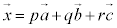 とするとき、内積
とするとき、内積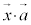 と
と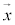 の大きさ
の大きさ をp,q,rを用いて表すと、
をp,q,rを用いて表すと、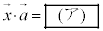 ,
,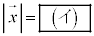 である。
である。
(ii) 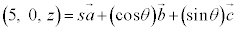 を満たす実数s,θが存在するような実数zは2個あるが、それらをすべて求めると
を満たす実数s,θが存在するような実数zは2個あるが、それらをすべて求めると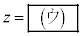 である。
である。
(2) n を奇数とする。nと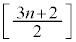 の積が6の倍数であるための必要十分条件は、nを
の積が6の倍数であるための必要十分条件は、nを で割ったときの余りが
で割ったときの余りが となることである。ただし、実数xに対しxを超えない最大の整数を
となることである。ただし、実数xに対しxを超えない最大の整数を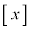 と表す。また、
と表す。また、 ,
,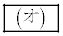 は
は を満たす整数である。
を満たす整数である。 ,
,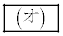 を求める過程を解答欄(2)に記述しなさい。
を求める過程を解答欄(2)に記述しなさい。
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
解答 計算が大変にならないように工夫されていて一本道です。あっさり仕上げてしまいましょう。空所補充問題なので、勿論、(2)では十分性の確認は不要です。
(i) 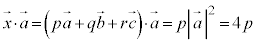 ......[ア]
......[ア] ∴ 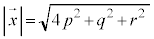 ......[イ]
......[イ]
(2) mを整数として、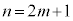 とおくと、
とおくと、 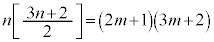 が6の倍数(整数を参照)なので、kを整数として、
が6の倍数(整数を参照)なので、kを整数として、これより、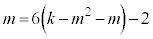 ,整数jを
,整数jを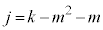 とおくと、
とおくと、 ∴ 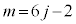
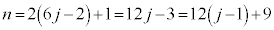
よって、nを12で割ったときの余りは9です。
逆に、lを整数として、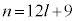 とおくと、
とおくと、 よって、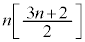 は6の倍数です。
は6の倍数です。
即ち、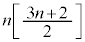 が6の倍数であるための必要十分条件は、nを12で割ったときの余りが9となることです。12 ......[エ],9 ......[オ]
が6の倍数であるための必要十分条件は、nを12で割ったときの余りが9となることです。12 ......[エ],9 ......[オ]
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
慶大理工数学TOP 数学TOP TOPページに戻る
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
各問題の著作権は
出題大学に属します。©2005-2024(有)りるらる 苦学楽学塾 随時入会受付中!理系大学受験ネット塾苦学楽学塾(ご案内はこちら)ご入会は、
まず、こちらまでメールを
お送りください。