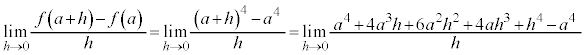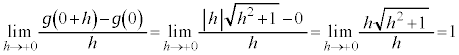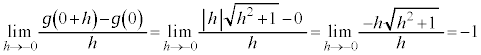慶大理工数学'23年[1]
(1) 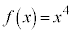 とする。
とする。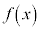 の
の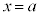 における微分係数を、定義に従って求めなさい。計算過程も記述しなさい。
における微分係数を、定義に従って求めなさい。計算過程も記述しなさい。
(2) 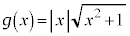 とする。
とする。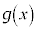 が
が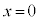 で微分可能でないことを証明しなさい。
で微分可能でないことを証明しなさい。
(3) 閉区間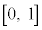 上で定義された連続関数
上で定義された連続関数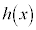 が、開区間
が、開区間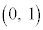 で微分可能であり、この区間で常に
で微分可能であり、この区間で常に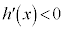 であるとする。このとき、
であるとする。このとき、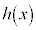 が区間
が区間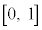 で減少することを、平均値の定理を用いて証明しなさい。
で減少することを、平均値の定理を用いて証明しなさい。
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
解答 教科書をどれだけよく読んでいたか、という問題です。
(1) 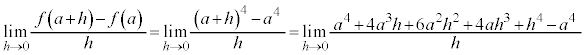
よって、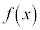 の
の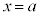 における微分係数
における微分係数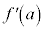 は、
は、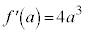 ......[答]
......[答]
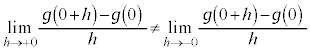 より、
より、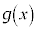 は
は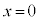 において、微分可能ではありません(微分・導関数を参照)。(証明終)
において、微分可能ではありません(微分・導関数を参照)。(証明終)
(3) 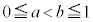 として、平均値の定理より、
として、平均値の定理より、
を満たす実数cが存在します。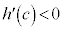 ,
,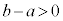 より、
より、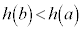 です。
です。
よって、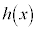 は区間
は区間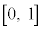 で減少します(関数の増減を参照)。(証明終)
で減少します(関数の増減を参照)。(証明終)
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
慶大理工数学TOP 数学TOP TOPページに戻る
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
各問題の著作権は
出題大学に属します。©2005-2024(有)りるらる 苦学楽学塾 随時入会受付中!理系大学受験ネット塾苦学楽学塾(ご案内はこちら)ご入会は、
まず、こちらまでメールを
お送りください。