慶應大学理工学部2023年数学入試問題
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
[1](1) 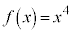 とする。
とする。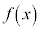 の
の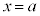 における微分係数を、定義に従って求めなさい。計算過程も記述しなさい。
における微分係数を、定義に従って求めなさい。計算過程も記述しなさい。
(2) 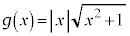 とする。
とする。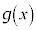 が
が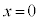 で微分可能でないことを証明しなさい。
で微分可能でないことを証明しなさい。
(3) 閉区間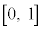 上で定義された連続関数
上で定義された連続関数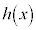 が、開区間
が、開区間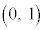 で微分可能であり、この区間で常に
で微分可能であり、この区間で常に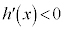 であるとする。このとき、
であるとする。このとき、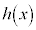 が区間
が区間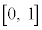 で減少することを、平均値の定理を用いて証明しなさい。
で減少することを、平均値の定理を用いて証明しなさい。 [解答へ]
[2] kを正の実数とし、空間内に点O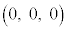 ,A
,A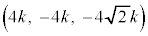 ,B
,B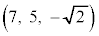 をとる。点CはO,A,Bを含む平面上の点であり、
をとる。点CはO,A,Bを含む平面上の点であり、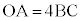 で、四角形OACBはOAを底辺とする台形であるとする。
で、四角形OACBはOAを底辺とする台形であるとする。
(1) 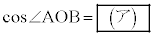 である。台形OACBの面積をkを用いて表すと
である。台形OACBの面積をkを用いて表すと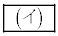 となる。また、線分ACの長さをkを用いて表すと
となる。また、線分ACの長さをkを用いて表すと となる。
となる。
(2) 台形OACBが円に内接するとき、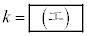 である。
である。
(3) 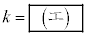 であるとし、直線OBと直線ACの交点をDとする。△OBPと△ACPの面積が等しい、という条件を満たす空間内の点P全体は、点Dを通る2つの平面上の点全体から点Dを除いたものになる。これら2つの平面のうち、線分OAと交わらないものをαとする。点Oから平面αに下ろした垂線の長さは
であるとし、直線OBと直線ACの交点をDとする。△OBPと△ACPの面積が等しい、という条件を満たす空間内の点P全体は、点Dを通る2つの平面上の点全体から点Dを除いたものになる。これら2つの平面のうち、線分OAと交わらないものをαとする。点Oから平面αに下ろした垂線の長さは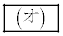 である。
である。 [解答へ]
[3] 何も入っていない2つの袋A,Bがある。いま、「硬貨を1枚投げて表が出たら袋A,裏が出たら袋Bを選び、以下のルールに従って選んだ袋の中に玉を入れる」という操作を繰り返す。
−−ルール−−−−−−−−−−−−−−−−−−−−−
●選んだ袋の中に入っている玉の数がもう一方の袋の中に入っている玉の数より多いか、2つの袋の中に入っている玉の数が同じとき、選んだ袋の中に玉を1個入れる。
●選んだ袋の中に入っている玉の数がもう一方の袋の中に入っている玉の数より少ないとき、選んだ袋の中に入っている玉の数が、もう一方の袋の中に入っている玉の数と同じになるまで選んだ袋の中に玉を入れる。
−−−−−−−−−−−−−−−−−−−−−−−−−−
たとえば、上の操作を3回行ったとき、硬貨が順に表、表、裏と出たとすると、A,B2つの袋の中の玉の数は次のように変化する。
(1) 4回目の操作を終えたとき、袋Aの中に3個以上の玉が入っている確率は である。また、4回目の操作を終えた時点で袋Aの中に3個以上の玉が入っているという条件の下で、7回目の操作を終えたとき袋Bの中に入っている玉の数が3個以下である条件付確率は
である。また、4回目の操作を終えた時点で袋Aの中に3個以上の玉が入っているという条件の下で、7回目の操作を終えたとき袋Bの中に入っている玉の数が3個以下である条件付確率は である。
である。
(2) n回目の操作を終えたとき、袋Aの中に入っている玉の数のほうが、袋Bの中に入っている玉の数よりも多い確率を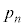 とする。
とする。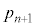 を
を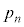 を用いて表すと、
を用いて表すと、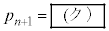 となり、これより
となり、これより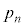 をnを用いて表すと
をnを用いて表すと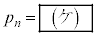 となる。
となる。
(3) n回目(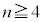 )の操作を終えたとき、袋Aの中に
)の操作を終えたとき、袋Aの中に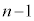 個以上の玉が入っている確率は
個以上の玉が入っている確率は であり、
であり、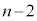 個以上の玉が入っている確率は
個以上の玉が入っている確率は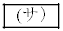 である。
である。 [解答へ]
[4](1) 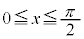 において常に不等式
において常に不等式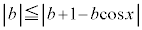 が成り立つような実数bの値の範囲は
が成り立つような実数bの値の範囲は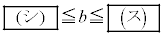 である。
である。
以下、bを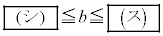 を満たす0でない実数とし、数列
を満たす0でない実数とし、数列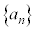 を、
を、
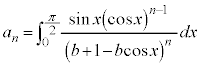 (
(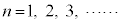 )
)
(2) 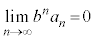 が成り立つことを証明しなさい。
が成り立つことを証明しなさい。
(3) 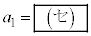 である。
である。
(5) 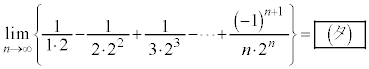 である。
である。 [解答へ]
[5](1) αを ではない複素数とする。複素数平面上で
ではない複素数とする。複素数平面上で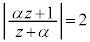 を満たす点z全体からなる図形をCとする。Cはαが
を満たす点z全体からなる図形をCとする。Cはαが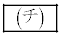 を満たすとき直線となり、
を満たすとき直線となり、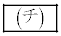 を満たさないとき円となる。αが
を満たさないとき円となる。αが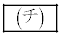 を満たさないとき、円Cの中心をαを用いて表すと
を満たさないとき、円Cの中心をαを用いて表すと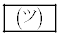 となる。αが
となる。αが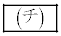 を満たすとき、直線C上の点zのうち、その絶対値が最小となるものをαを用いて表すと
を満たすとき、直線C上の点zのうち、その絶対値が最小となるものをαを用いて表すと となる。
となる。
(2) 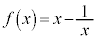 とする。自然数a,b,cの組で、
とする。自然数a,b,cの組で、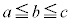 かつ
かつ が自然数であるものの総数は、
が自然数であるものの総数は、 個である。その中で
個である。その中で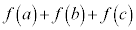 の値が最大になるのは
の値が最大になるのは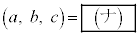 のときである。
のときである。 [解答へ]
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
慶大理工数学TOP 数学TOP TOPページに戻る
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
各問題の著作権は
出題大学に属します。©2005-2024(有)りるらる 苦学楽学塾 随時入会受付中!理系大学受験ネット塾苦学楽学塾(ご案内はこちら)ご入会は、
まず、こちらまでメールを
お送りください。 
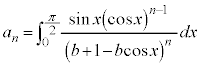 (
(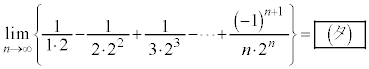 である。
である。