�c�嗝�H���w'23�N[5]
(1) α��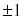 �ł͂Ȃ����f���Ƃ���B���f�����ʏ��
�ł͂Ȃ����f���Ƃ���B���f�����ʏ��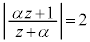 �����_z�S�̂���Ȃ�}�`��C�Ƃ���BC��α��
�����_z�S�̂���Ȃ�}�`��C�Ƃ���BC��α��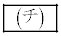 �����Ƃ������ƂȂ�A
�����Ƃ������ƂȂ�A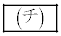 �����Ȃ��Ƃ��~�ƂȂ�Bα��
�����Ȃ��Ƃ��~�ƂȂ�Bα��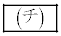 �����Ȃ��Ƃ��A�~C�̒��S��α��p���ĕ\����
�����Ȃ��Ƃ��A�~C�̒��S��α��p���ĕ\����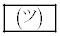 �ƂȂ�Bα��
�ƂȂ�Bα��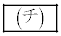 �����Ƃ��A����C��̓_z�̂����A���̐�Βl���ŏ��ƂȂ���̂�α��p���ĕ\����
�����Ƃ��A����C��̓_z�̂����A���̐�Βl���ŏ��ƂȂ���̂�α��p���ĕ\���� �ƂȂ�B
�ƂȂ�B
(2) 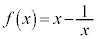 �Ƃ���B���R��a�Cb�Cc�̑g�ŁA
�Ƃ���B���R��a�Cb�Cc�̑g�ŁA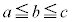 ����
����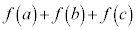 �����R���ł�����̂̑����́A
�����R���ł�����̂̑����́A �ł���B���̒���
�ł���B���̒���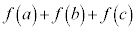 �̒l���ő�ɂȂ�̂�
�̒l���ő�ɂȂ�̂�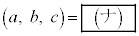 �̂Ƃ��ł���B
�̂Ƃ��ł���B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@(1)��(2)�͗ގ����镔���͂���܂����A�֘A�͂���܂���B(1)�͏��ɉ��Ȃ��ƌv�Z����ςł�(���f�����������f�����ʂ̐}�`�I���p���Q��)�B(2)�́A�ŏ��̎��R����1�ł���A�Ƃ���������p���āA�͈͂��i������ő�������Œ��ׂ�A�Ƃ��������̓T�^���ł��B
(1) C�F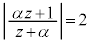 ���A
���A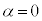 �̂Ƃ��A
�̂Ƃ��A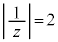 �܂�
�܂�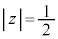 �C����͌��_�𒆐S�Ƃ��锼�a
�C����͌��_�𒆐S�Ƃ��锼�a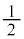 �̉~�ł��B
�̉~�ł��B 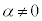 �̂Ƃ��A
�̂Ƃ��A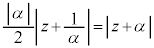 �@����@
�@����@�E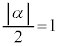 �C�܂�
�C�܂�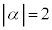 �̂Ƃ��Az��2�_
�̂Ƃ��Az��2�_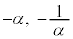 ���瓙�����ɂ���_��\���Az�S�̂́A2�_�����Ԑ����̐��������ł��B
���瓙�����ɂ���_��\���Az�S�̂́A2�_�����Ԑ����̐��������ł��B �E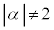 �̂Ƃ��Az��2�_
�̂Ƃ��Az��2�_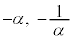 ����̋����̔䂪
����̋����̔䂪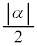 �F1�ł���_��\���Az�S�̂̓A�|���j�E�X�̉~�ƂȂ�A���̉~�́A2�_
�F1�ł���_��\���Az�S�̂̓A�|���j�E�X�̉~�ƂȂ�A���̉~�́A2�_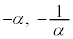 ��
��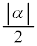 �F1�ɓ�������_A�ƊO������_B�a�̗��[�Ƃ���~�ŁA���S��AB�̒��_�ł��B
�F1�ɓ�������_A�ƊO������_B�a�̗��[�Ƃ���~�ŁA���S��AB�̒��_�ł��B �_A�́A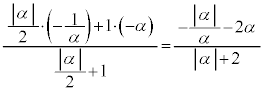
�_B�́A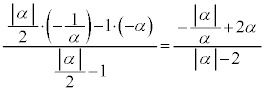
�~�̒��S�A����AB�̒��_�́A C�������ɂȂ�̂́A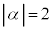 .....[�`]�@�̂Ƃ��BC���~�ɂȂ�Ƃ��A���S�́A
.....[�`]�@�̂Ƃ��BC���~�ɂȂ�Ƃ��A���S�́A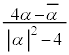 ......[�c]
......[�c]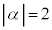 ��C�������ɂȂ�Ƃ��A�@���A
��C�������ɂȂ�Ƃ��A�@���A 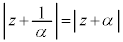
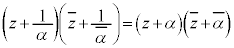
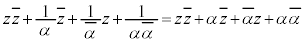
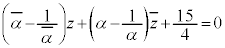 �@����A�@(��
�@����A�@(�� 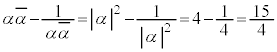 )
)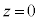 �͇A�������A����C�͌��_��ʂ�܂���B����C��̓_z��
�͇A�������A����C�͌��_��ʂ�܂���B����C��̓_z��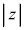 ���ŏ��ɂ���_�́A���_��ʂ蒼��C�Ɛ����Ȓ����ƒ���C�Ƃ̌�_�ł��B
���ŏ��ɂ���_�́A���_��ʂ蒼��C�Ɛ����Ȓ����ƒ���C�Ƃ̌�_�ł��B
����C��2�_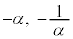 �����Ԑ����̐��������Ȃ̂ŁA2�_
�����Ԑ����̐��������Ȃ̂ŁA2�_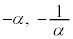 �����Ԓ����Ɛ����ł��B2�_
�����Ԓ����Ɛ����ł��B2�_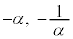 �����Ԓ����ƕ��s�Ō��_��ʂ钼����̓_z�́At �������Ƃ��āA
�����Ԓ����ƕ��s�Ō��_��ʂ钼����̓_z�́At �������Ƃ��āA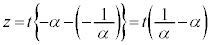 �@����B
�@����B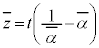 �@����C
�@����C�B�C�C���A�ɑ������ƁA
�B�ɑ�����A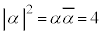 ��p���āA
��p���āA 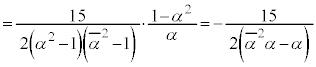
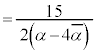 ......[�e]
......[�e]
(2) 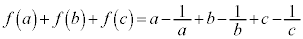 �����R���ƂȂ�Ƃ��A
�����R���ƂȂ�Ƃ��A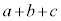 �����R���Ȃ̂ŁA
�����R���Ȃ̂ŁA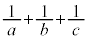 �����R���ł��B
�����R���ł��B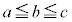 ���
���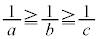 �Ȃ̂ŁA
�Ȃ̂ŁA �ł������Ȏ��R����1�Ȃ̂ŁA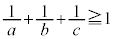 �ł���A
�ł���A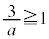 �C�����A
�C�����A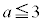 �ł��B����ŁA
�ł��B����ŁA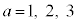 �Ɍ����܂��B
�Ɍ����܂��B �E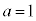 �̂Ƃ��A
�̂Ƃ��A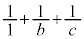 �����R���Ȃ̂ŁA
�����R���Ȃ̂ŁA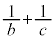 (
(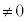 )�����R���ł��B
)�����R���ł��B �ł������Ȏ��R����1�Ȃ̂ŁA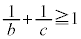 �ł���A
�ł���A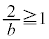 �C�����A
�C�����A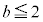 �ŁA
�ŁA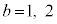 �Ɍ����܂��B
�Ɍ����܂��B
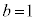 �̂Ƃ��A
�̂Ƃ��A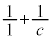 �͎��R���ł����A�����Ȃ鎩�R��c�́A
�͎��R���ł����A�����Ȃ鎩�R��c�́A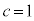 �����ł�(
�����ł�(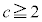 �̂Ƃ��A
�̂Ƃ��A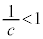 �ł����āA
�ł����āA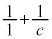 �͎��R���ɂȂ蓾�܂���)�B
�͎��R���ɂȂ蓾�܂���)�B
����āA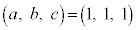 �C
�C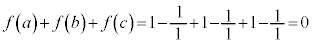
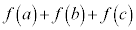 �����R���ɂȂ炸�s�K�ł��B
�����R���ɂȂ炸�s�K�ł��B
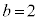 �̂Ƃ��A
�̂Ƃ��A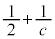 �͎��R���ł����A�����Ȃ鎩�R��c�́A
�͎��R���ł����A�����Ȃ鎩�R��c�́A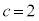 �����ł�(
�����ł�(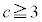 �̂Ƃ��A
�̂Ƃ��A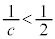 �C
�C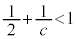 �ł����āA
�ł����āA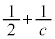 �͎��R���ɂȂ蓾�܂���)�B
�͎��R���ɂȂ蓾�܂���)�B
����āA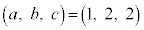 �C
�C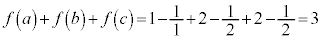
�E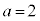 �̂Ƃ��A
�̂Ƃ��A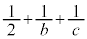 �����R���ł��B
�����R���ł��B �ł������Ȏ��R����1�Ȃ̂ŁA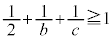 �ł���A
�ł���A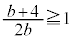 �C
�C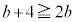 �C�����A
�C�����A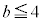 �ŁA
�ŁA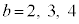 �Ɍ����܂��B
�Ɍ����܂��B
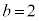 �̂Ƃ��A
�̂Ƃ��A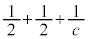 �����R���ł����A�����Ȃ鎩�R��c�́A
�����R���ł����A�����Ȃ鎩�R��c�́A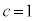 �����ł����A
�����ł����A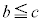 �������s�K�ł��B
�������s�K�ł��B
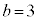 �̂Ƃ��A
�̂Ƃ��A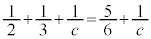 �����R���ł����A�����Ȃ鎩�R��c�́A
�����R���ł����A�����Ȃ鎩�R��c�́A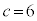 �����ł�(
�����ł�(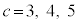 �̂Ƃ��A
�̂Ƃ��A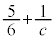 �͎��R���ł͂���܂���B
�͎��R���ł͂���܂���B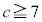 �̂Ƃ��A
�̂Ƃ��A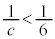 �C
�C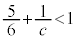 �ł����āA
�ł����āA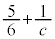 �͎��R���ɂȂ蓾�܂���)�B
�͎��R���ɂȂ蓾�܂���)�B
����āA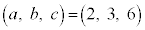 �C
�C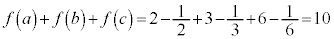
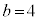 �̂Ƃ��A
�̂Ƃ��A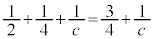 �����R���ł����A�����Ȃ鎩�R��c�́A
�����R���ł����A�����Ȃ鎩�R��c�́A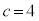 �����ł�(
�����ł�(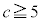 �̂Ƃ��A
�̂Ƃ��A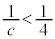 �C
�C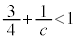 �ł����āA
�ł����āA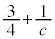 �͎��R���ɂȂ蓾�܂���)�B
�͎��R���ɂȂ蓾�܂���)�B
����āA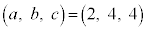 �C
�C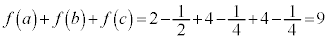
�E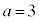 �̂Ƃ��A
�̂Ƃ��A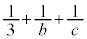 �����R���ł��B
�����R���ł��B �ł������Ȏ��R����1�Ȃ̂ŁA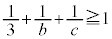 �ł���A
�ł���A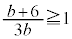 �C
�C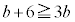 �C�����A
�C�����A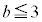 �ŁA
�ŁA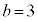 �Ɍ����܂��B���̂Ƃ��A
�Ɍ����܂��B���̂Ƃ��A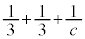 �����R���ɂȂ鎩�R��c�́A
�����R���ɂȂ鎩�R��c�́A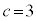 �����ł�(
�����ł�(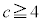 �̂Ƃ��A
�̂Ƃ��A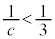 �C
�C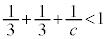 �ł����āA
�ł����āA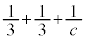 �͎��R���ɂȂ蓾�܂���)�B
�͎��R���ɂȂ蓾�܂���)�B
����āA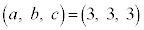 �C
�C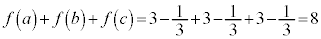
�ȏ���A���R��a�Cb�Cc�̑g�ŁA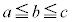 ����
����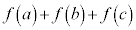 �����R���ł�����̂́A
�����R���ł�����̂́A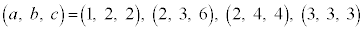 �ł���A���̑����́A4�� ......[�g]
�ł���A���̑����́A4�� ......[�g]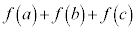 �̒l���ő�ɂȂ�̂́A
�̒l���ő�ɂȂ�̂́A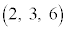 ......[�i]
......[�i]
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@�c�嗝�H���wTOP�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B 
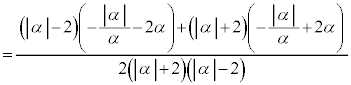
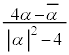 ......[�c]
......[�c]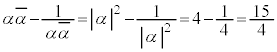 )
)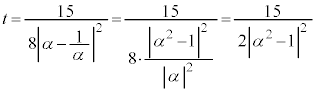 �@(�� [�`]���
�@(�� [�`]���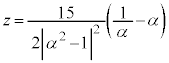
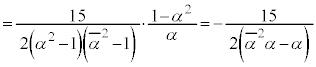
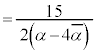 ......[�e]
......[�e]