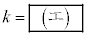
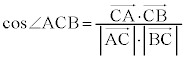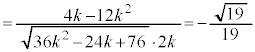�c�嗝�H���w'23�N[2]
k�𐳂̎����Ƃ��A��ԓ��ɓ_O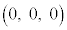 �CA
�CA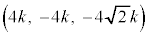 �CB
�CB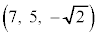 ���Ƃ�B�_C��O�CA�CB���܂ޕ��ʏ�̓_�ł���A
���Ƃ�B�_C��O�CA�CB���܂ޕ��ʏ�̓_�ł���A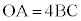 �ŁA�l�p�`OACB��OA���ӂƂ����`�ł���Ƃ���B
�ŁA�l�p�`OACB��OA���ӂƂ����`�ł���Ƃ���B
(1) 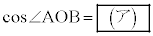 �ł���B��`OACB�̖ʐς�k��p���ĕ\����
�ł���B��`OACB�̖ʐς�k��p���ĕ\����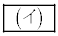 �ƂȂ�B�܂��A����AC�̒�����k��p���ĕ\����
�ƂȂ�B�܂��A����AC�̒�����k��p���ĕ\���� �ƂȂ�B
�ƂȂ�B
(2) ��`OACB���~�ɓ��ڂ���Ƃ��A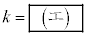 �ł���B
�ł���B
(3)  �ł���Ƃ��A����OB�ƒ���AC�̌�_��D�Ƃ���B��OBP�Ɓ�ACP�̖ʐς��������A�Ƃ�������������ԓ��̓_P�S�̂́A�_D��ʂ�2�̕��ʏ�̓_�S�̂���_D�����������̂ɂȂ�B�����2�̕��ʂ̂����A����OA�ƌ����Ȃ����̂�α�Ƃ���B�_O���畽��α�ɉ��낵�������̒�����
�ł���Ƃ��A����OB�ƒ���AC�̌�_��D�Ƃ���B��OBP�Ɓ�ACP�̖ʐς��������A�Ƃ�������������ԓ��̓_P�S�̂́A�_D��ʂ�2�̕��ʏ�̓_�S�̂���_D�����������̂ɂȂ�B�����2�̕��ʂ̂����A����OA�ƌ����Ȃ����̂�α�Ƃ���B�_O���畽��α�ɉ��낵�������̒����� �ł���B
�ł���B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@��ԃx�N�g���̊�{���ł����A���Ɍv�Z���܂��傤�B
(1) 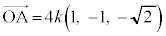 �@����@
�@����@ 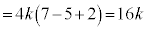 �@����C�@(�������Q��)
�@����C�@(�������Q��)�A�C�B�C�C���A
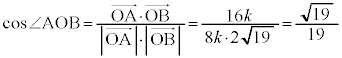 ......[�A]
......[�A]B���璼��OA�ɐ���BH�����낷�ƁA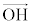 //
//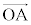 //
//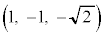 ���A
���A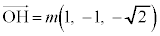 �Ƃ����ƁA
�Ƃ����ƁA 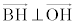 ���A
���A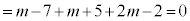 �@��
�@�� 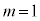
�� 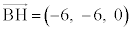 �C
�C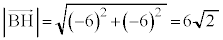 �@����D
�@����D ���D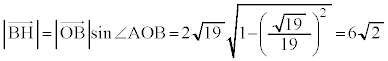 �ł��B
�ł��B 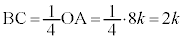 �@����E
�@����E���A��`�̖ʐς́A
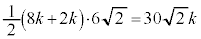 ......[�C]
......[�C]�܂��A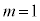 ���A
���A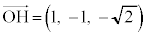 �@����F
�@����F 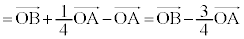 �@����G
�@����G�G���A�A�C�B�C�C��p���āA
�� 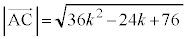 ......[�E]�@����H
......[�E]�@����H
(2) ��`���~�ɓ��ڂ���Ƃ��A�Ό�������p�͕�p���Ȃ�(�~�Ɛ}�`���Q��)�̂ŁA(1)�̌��ʂ��A 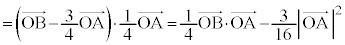 �@(�� �G)
�@(�� �G)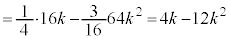 �@(�� �A�C�C)
�@(�� �A�C�C)������A�E�C�H��p���āA
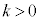 ���
��� �ł����āA�������2�悷��ƁA
�ł����āA�������2�悷��ƁA�܂��A�@�C�F���A
 �@����I
�@����I
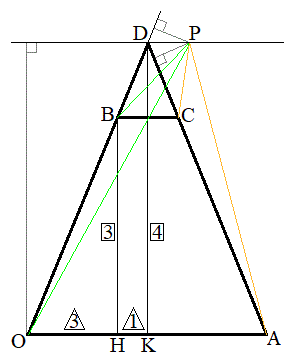 (3)
(3) 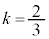 �̂Ƃ��H���A
�̂Ƃ��H���A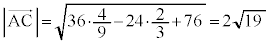 �C����ćB���
�C����ćB���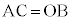 �ł�(�l�p�`OACB�͓��r��`)�B
�ł�(�l�p�`OACB�͓��r��`)�B��OBP = ��ACP���A�_P�́AOB�CAC�Ƃ̋������������Ȃ�A�_P�̑S�̂́A1�́A��OA�̐������ʂł��B�����OA�ƌ����̂ŕs�K�ł��B������́AOD��D���ւ̉�������P�Ƃ̋����ƁAP����AD�ɉ��낵�������̒������������ꍇ�ŁA����͓_D��ʂ�A��`OACB���܂ޖʂɐ����ȕ��ʂɂȂ�A���̕��ʂ�����α�ɂȂ�܂��B���̕��ʂ�OA�ƕ��s�Ȃ̂�OA�ƌ����܂���B����ȊO�ɁA��OBP = ��ACP�����}�`�͂���܂���B
�_D����OA�ɉ��낵�������̑���K�Ƃ���ƁAK��OA�̒��_�ŁA�I���A
��OBH �� ��ODK�C�E�}��OH�FOK = 3�F4���ABH�FDK = 3�F4�C�_O���畽��α�ɉ��낵�������̒�����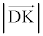 �ɓ������A�D���A
�ɓ������A�D���A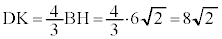 ......[�I]
......[�I]
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@�c�嗝�H���wTOP�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B 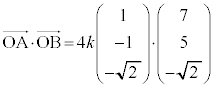
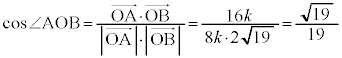 ......[�A]
......[�A]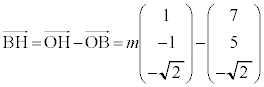
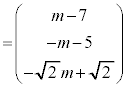
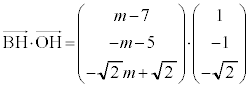
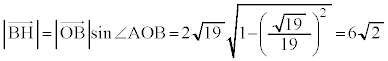 �ł��B
�ł��B