�c�嗝�H���w'23�N[3]
���������Ă��Ȃ�2�̑�A�CB������B���܁A�u�d�݂�1�������ĕ\���o�����A�C�����o�����B��I�сA�ȉ��̃��[���ɏ]���đI�܂̒��ɋʂ�����v�Ƃ���������J��Ԃ��B
�|�|���[���|�|�|�|�|�|�|�|�|�|�|�|�|�|�|�|�|�|�|�|�|
���I�܂̒��ɓ����Ă���ʂ̐�����������̑܂̒��ɓ����Ă���ʂ̐���葽�����A2�̑܂̒��ɓ����Ă���ʂ̐��������Ƃ��A�I�܂̒��ɋʂ�1�����B
���I�܂̒��ɓ����Ă���ʂ̐�����������̑܂̒��ɓ����Ă���ʂ̐���菭�Ȃ��Ƃ��A�I�܂̒��ɓ����Ă���ʂ̐����A��������̑܂̒��ɓ����Ă���ʂ̐��Ɠ����ɂȂ�܂őI�܂̒��ɋʂ�����B
�|�|�|�|�|�|�|�|�|�|�|�|�|�|�|�|�|�|�|�|�|�|�|�|�|�|
���Ƃ��A��̑����3��s�����Ƃ��A�d�݂����ɕ\�A�\�A���Əo���Ƃ���ƁAA�CB2�̑܂̒��̋ʂ̐��͎��̂悤�ɕω�����B
(1) 4��ڂ̑�����I�����Ƃ��A��A�̒���3�ȏ�̋ʂ������Ă���m���� �ł���B�܂��A4��ڂ̑�����I�������_�ő�A�̒���3�ȏ�̋ʂ������Ă���Ƃ��������̉��ŁA7��ڂ̑�����I�����Ƃ���B�̒��ɓ����Ă���ʂ̐���3�ȉ��ł�������t�m����
�ł���B�܂��A4��ڂ̑�����I�������_�ő�A�̒���3�ȏ�̋ʂ������Ă���Ƃ��������̉��ŁA7��ڂ̑�����I�����Ƃ���B�̒��ɓ����Ă���ʂ̐���3�ȉ��ł�������t�m���� �ł���B
�ł���B
(2) n��ڂ̑�����I�����Ƃ��A��A�̒��ɓ����Ă���ʂ̐��̂ق����A��B�̒��ɓ����Ă���ʂ̐����������m����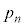 �Ƃ���B
�Ƃ���B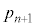 ��
��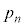 ��p���ĕ\���ƁA
��p���ĕ\���ƁA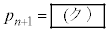 �ƂȂ�A������
�ƂȂ�A������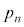 ��n��p���ĕ\����
��n��p���ĕ\����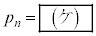 �ƂȂ�B
�ƂȂ�B
(3) n���(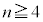 )�̑�����I�����Ƃ��A��A�̒���
)�̑�����I�����Ƃ��A��A�̒���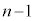 �ȏ�̋ʂ������Ă���m����
�ȏ�̋ʂ������Ă���m���� �ł���A
�ł���A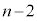 �ȏ�̋ʂ������Ă���m����
�ȏ�̋ʂ������Ă���m����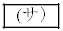 �ł���B
�ł���B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@���ł��B����(3)�́A���Ȃ��܂�I�Ƃ��ɂ͑������Ɠ����ɂ���A�Ƃ������[����2�߂�����ɕ��G�ɂ��Ă��āA�J�ڐ}���珑���ɂ��������Ă��܂��B����ɁA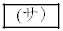 �ł́A��A��
�ł́A��A��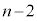 �ȏ�ɂȂ�ꍇ�̒��ɁA��B��
�ȏ�ɂȂ�ꍇ�̒��ɁA��B��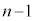 �̏ꍇ(��B�̕�������)���܂܂�邱�Ƃ�����₱�������Ă��܂��B�������ł���Ȑ��_�I�]�T�����Ă邩�A�Ƃ������Ƃ͂���܂����A�ł���A�����(3)���̂ĂĂł��A(1)�ŐT�d�Ɏ��`�}�������Ċm���ɓ��_�������Ƃ���ł��B
�̏ꍇ(��B�̕�������)���܂܂�邱�Ƃ�����₱�������Ă��܂��B�������ł���Ȑ��_�I�]�T�����Ă邩�A�Ƃ������Ƃ͂���܂����A�ł���A�����(3)���̂ĂĂł��A(1)�ŐT�d�Ɏ��`�}�������Ċm���ɓ��_�������Ƃ���ł��B
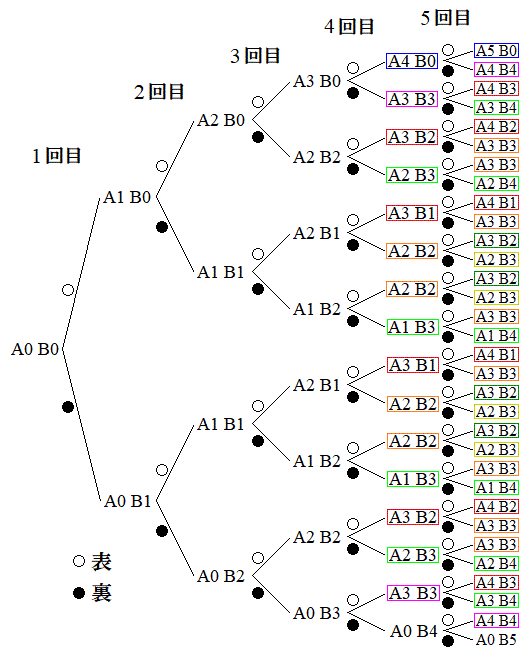
(1) �E�}���`�}(�g�̐F�ɂ��ẮA(3)�Ő������܂�)�ŁA4��ڑ����̐g(1)�C�Ԙg(4)�C�s���N�g(2)�̐��𐔂��āA4��ڂ̑�����I�����Ƃ��A��A�̒���3�ȏ�̋ʂ������Ă����m���́A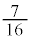 ......[�J]
......[�J] 4��ڑ����A��A�̒���3�ȏ�̋ʂ������Ă����Ƃ��An��ڑ����̑�B���̋ʂ̌���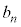 �Ƃ��܂��B
�Ƃ��܂��B
���̂Ƃ��A4��ڈȍ~(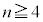 )�A��B���̋ʂ̌���4�ȏ�(
)�A��B���̋ʂ̌���4�ȏ�(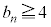 )�ɂȂ��
)�ɂȂ��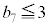 �ɂȂ邱�Ƃ͂���܂���B
�ɂȂ邱�Ƃ͂���܂���B �E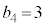 �ƂȂ�m���͉E�}���`�}���
�ƂȂ�m���͉E�}���`�}���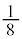 �C���̂Ƃ�
�C���̂Ƃ�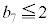 �ƂȂ邱�Ƃ͂Ȃ��A
�ƂȂ邱�Ƃ͂Ȃ��A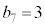 �ƂȂ�̂́A5��ځA6��ځA7��ځA��������\���o���ꍇ�ŁA�����m����
�ƂȂ�̂́A5��ځA6��ځA7��ځA��������\���o���ꍇ�ŁA�����m����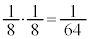 �ł��B
�ł��B �E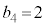 �ƂȂ�m���͉E�}���`�}���
�ƂȂ�m���͉E�}���`�}���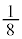 �C���̂Ƃ�
�C���̂Ƃ�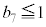 �ƂȂ邱�Ƃ͂Ȃ��A
�ƂȂ邱�Ƃ͂Ȃ��A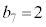 �ƂȂ�̂́A5��ځA6��ځA7��ځA��������\���o���ꍇ�ŁA�����m����
�ƂȂ�̂́A5��ځA6��ځA7��ځA��������\���o���ꍇ�ŁA�����m����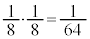 �ł��B
�ł��B 5��ڂɗ����o��ƁA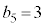 �ɂȂ�܂��B���̂Ƃ��A
�ɂȂ�܂��B���̂Ƃ��A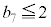 �ƂȂ邱�Ƃ͂Ȃ��A
�ƂȂ邱�Ƃ͂Ȃ��A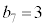 �ɂȂ�̂́A6��ځA7��ڂɕ\���o���ꍇ�ŁA�����m����
�ɂȂ�̂́A6��ځA7��ڂɕ\���o���ꍇ�ŁA�����m����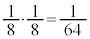 �@����@
�@����@
���D5��ڕ\�̂Ƃ��́AA��4�ȏ�ɂȂ��Ă��܂��̂ŁA6��ځA7��ڂɗ����o�Ă��A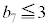 �ɂȂ�Ȃ��B
�ɂȂ�Ȃ��B �E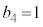 �ƂȂ�m���͉E�}���`�}���
�ƂȂ�m���͉E�}���`�}���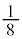 �C���̂Ƃ��A
�C���̂Ƃ��A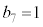 �ƂȂ�̂́A5��ځA6��ځA7��ځA��������\���o���ꍇ�ŁA���̊m����
�ƂȂ�̂́A5��ځA6��ځA7��ځA��������\���o���ꍇ�ŁA���̊m����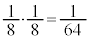
5��ڂɗ����o��ƁA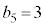 �ɂȂ�܂��B�Ȍ�͇@�Ɠ����ŁA
�ɂȂ�܂��B�Ȍ�͇@�Ɠ����ŁA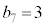 �ƂȂ��m����
�ƂȂ��m����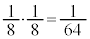
���D������A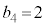 �Ɠ��l�A5��ڂɕ\���o���A��4�ȏ�ɂȂ�A6��ځA7��ڂɗ����o�Ă��A
�Ɠ��l�A5��ڂɕ\���o���A��4�ȏ�ɂȂ�A6��ځA7��ڂɗ����o�Ă��A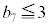 �ɂȂ�Ȃ��B
�ɂȂ�Ȃ��B �E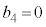 �ƂȂ�m���͉E�}���`�}���
�ƂȂ�m���͉E�}���`�}���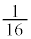 �C5��ڂɗ����o���
�C5��ڂɗ����o���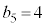 �ɂȂ�̂ŁA
�ɂȂ�̂ŁA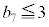 �ɂȂ�̂́A5��ځA6��ځA7��ځA��������\���o���ꍇ�ŁA�����m����
�ɂȂ�̂́A5��ځA6��ځA7��ځA��������\���o���ꍇ�ŁA�����m����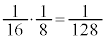 �ł��B
�ł��B 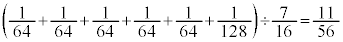 ......[�L]
......[�L]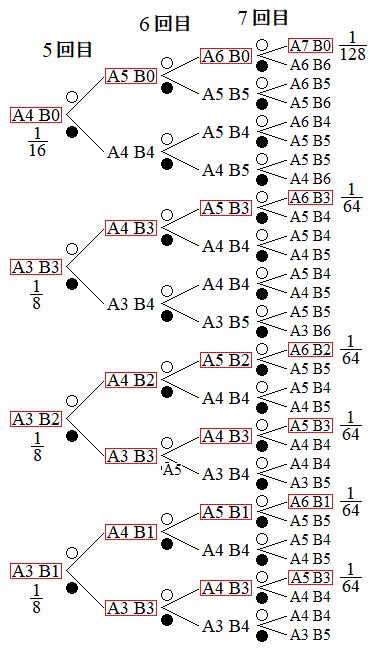 �ʉ��D��L�̂悤�Ȃ��ƂɂȂ�Ȃ�A�_���I�ɐi�߂�����A�E���}���`�}�������Đ�����������N�ł��B
�ʉ��D��L�̂悤�Ȃ��ƂɂȂ�Ȃ�A�_���I�ɐi�߂�����A�E���}���`�}�������Đ�����������N�ł��B
(2) n��ڂ̑����A��A���̋ʂ̐�����B���̋ʂ̐����������m����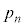 �Ƃ���ƁA��B���̋ʂ̐�����A���̋ʂ̐����������m����
�Ƃ���ƁA��B���̋ʂ̐�����A���̋ʂ̐����������m����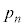 �ƂȂ�܂��B�܂��A��A���̋ʂ̐�����B���̋ʂ̐��Ɠ������Ȃ�m���́A
�ƂȂ�܂��B�܂��A��A���̋ʂ̐�����B���̋ʂ̐��Ɠ������Ȃ�m���́A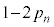 �ł��B
�ł��B 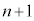 ��ڂ̑����A��A���̋ʂ̐�����B���̋ʂ̐����������Ȃ�̂́An��ڂ̑����A��A���̋ʂ̐�����B���̋ʂ̐������������A�������ꍇ�ɁA
��ڂ̑����A��A���̋ʂ̐�����B���̋ʂ̐����������Ȃ�̂́An��ڂ̑����A��A���̋ʂ̐�����B���̋ʂ̐������������A�������ꍇ�ɁA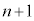 ��ڂŕ\���o��Ƃ��ł��B���̊m����(2���ԑQ�������Q��)�A
��ڂŕ\���o��Ƃ��ł��B���̊m����(2���ԑQ�������Q��)�A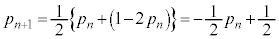 ......[�N]�@����A
......[�N]�@����A
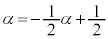 �@����B�@�Ƃ���ƁA
�@����B�@�Ƃ���ƁA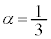
�A�|�B���A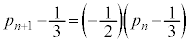
������A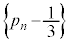 �́A����F
�́A����F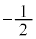 �C�����F
�C�����F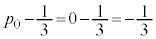 �����䐔���ł��B����āA
�����䐔���ł��B����āA 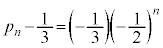 �@��
�@�� 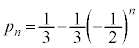 ......[�P]
......[�P]
(3) �J�ڐ}���������Q��������肽���Ƃ���ł����A���ǂ̂悤�ɕ����čl���邩�Y�݂܂��B�����ł́A�㑤�̎��`�}��4��ڑ���ォ��5��ڑ����ւ̑J�ڂɂ��čl���邱�Ƃɂ��܂��B�܂��An���A�\���o�������ꍇ(�g)���čl����ׂ��ł��傤�B�܂��An��ڑ����ɁA��A�Ƒ�B���Ƃ���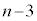 �ȉ��ɂȂ��Ă��܂��ƁA
�ȉ��ɂȂ��Ă��܂��ƁA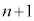 ��ڂɕ\���o�Ă������o�Ă��A
��ڂɕ\���o�Ă������o�Ă��A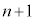 ��ڑ����ɑ�A����B���Ƃ���
��ڑ����ɑ�A����B���Ƃ���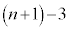 �ȉ��ɂȂ�A��A����B��
�ȉ��ɂȂ�A��A����B��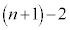 �ɂȂ�Ȃ����Ƃɒ��ӂ��܂��B
�ɂȂ�Ȃ����Ƃɒ��ӂ��܂��B 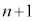 ��ڑ�����
��ڑ����� �ȏ�ɂȂ�Ƃ��An��ڑ����ɂǂ������ɂȂ��Ă��邩���l���܂��B�܂��A��A��
�ȏ�ɂȂ�Ƃ��An��ڑ����ɂǂ������ɂȂ��Ă��邩���l���܂��B�܂��A��A��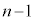 �ő�B��
�ő�B��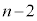 �ȉ��ƂȂ�ꍇ(�Ԙg)�ƁA��A�Ƒ�B���Ƃ���
�ȉ��ƂȂ�ꍇ(�Ԙg)�ƁA��A�Ƒ�B���Ƃ���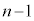 �̏ꍇ(�s���N�̘g)������܂��B
�̏ꍇ(�s���N�̘g)������܂��B
�܂��A��A��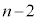 �ő�B��
�ő�B��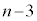 �ȉ��ƂȂ�ꍇ(�Θg�A4��ڑ����ɂ͏o�Ă��܂���)�Ƒ�A�Ƒ�B���Ƃ���
�ȉ��ƂȂ�ꍇ(�Θg�A4��ڑ����ɂ͏o�Ă��܂���)�Ƒ�A�Ƒ�B���Ƃ���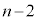 �̏ꍇ(�I�����W�F�̘g)������܂��B
�̏ꍇ(�I�����W�F�̘g)������܂��B
�܂��A��A�̋ʂ̐��ƁA��B�̋ʂ̐����Ώ̐���L���邱�Ƃɒ��ӂ��܂��B
��A����B�̕����������ΐF�̘g����I�����W�F�̘g�ɑJ�ڂ���ꍇ������܂��Bn��ڑ����ɁA�E��A�̋ʂ̐���n�ɂȂ�̂́An��S�ĕ\���o��ꍇ�ŁA���̊m����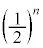 �C���l�ɁA��B�̋ʂ̐���n�ɂȂ�m����
�C���l�ɁA��B�̋ʂ̐���n�ɂȂ�m����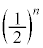 �ł��B�@����C
�ł��B�@����C �E��A�̋ʂ̐���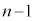 �A��B�̋ʂ̐���1�ȏ�
�A��B�̋ʂ̐���1�ȏ�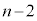 �ȉ��ɂȂ�ꍇ��(
�ȉ��ɂȂ�ꍇ��(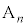 )�C���̊m����
)�C���̊m����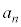 �Ƃ��܂��B��B�̋ʂ̐���
�Ƃ��܂��B��B�̋ʂ̐���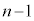 �A��A�̋ʂ̐���1�ȏ�
�A��A�̋ʂ̐���1�ȏ�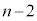 �ȉ��ɂȂ�m����
�ȉ��ɂȂ�m����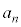 �ł��B
�ł��B �E��A�̋ʂ̐��Ƒ�B�̋ʂ̐���������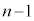 �ɂȂ�ꍇ��(
�ɂȂ�ꍇ��(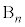 )�C���̊m����
)�C���̊m����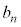 �Ƃ��܂�((1)��
�Ƃ��܂�((1)��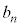 �Ƃ͈قȂ�܂�)�B
�Ƃ͈قȂ�܂�)�B �E��A�̋ʂ̐���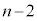 �A��B�̋ʂ̐���1�ȏ�
�A��B�̋ʂ̐���1�ȏ�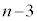 �ȉ��ɂȂ�ꍇ��(
�ȉ��ɂȂ�ꍇ��(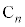 )�C���̊m����
)�C���̊m����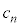 �Ƃ��܂��B��B�̋ʂ̐���
�Ƃ��܂��B��B�̋ʂ̐���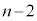 �A��A�̋ʂ̐���1�ȏ�
�A��A�̋ʂ̐���1�ȏ�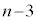 �ȉ��ɂȂ�m����
�ȉ��ɂȂ�m����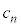 �ł��B
�ł��B �E��A�̋ʂ̐��Ƒ�B�̋ʂ̐���������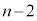 �ɂȂ�ꍇ��(
�ɂȂ�ꍇ��(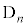 )�C���̊m����
)�C���̊m����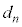 �Ƃ��܂��B
�Ƃ��܂��B n��S�ĕ\�܂��͗��ƂȂ�ꍇ��(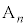 )�C(
)�C(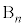 )�C(
)�C(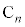 )�C(
)�C(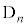 )�͔r���ł��B
)�͔r���ł��B 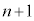 ��ڑ����A
��ڑ����A�E��(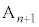 )�ɂȂ�̂́A��(
)�ɂȂ�̂́A��(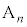 )���邢�͏�(
)���邢�͏�(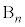 )�ɂ����āA�\���o��ꍇ�ł�(��̎��`�}�ŁA5��ڂ̐Ԙg�����Ă�������)�B���̊m��
)�ɂ����āA�\���o��ꍇ�ł�(��̎��`�}�ŁA5��ڂ̐Ԙg�����Ă�������)�B���̊m��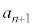 �́A
�́A 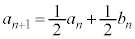 �@����D
�@����D�E��(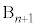 )�ɂȂ�̂́An��ڂ܂ŕ\���o�āA
)�ɂȂ�̂́An��ڂ܂ŕ\���o�āA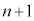 ��ڂɗ����o��ꍇ�A���邢�́An��ڂ܂ŗ����o�āA
��ڂɗ����o��ꍇ�A���邢�́An��ڂ܂ŗ����o�āA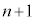 ��ڂɕ\���o��ꍇ�ł�(��̎��`�}�ŁA5��ڂ̃s���N�̘g�����Ă�������)�B���̊m��
��ڂɕ\���o��ꍇ�ł�(��̎��`�}�ŁA5��ڂ̃s���N�̘g�����Ă�������)�B���̊m��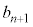 �́A
�́A 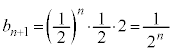 �@����E
�@����E�E��(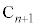 )�ɂȂ�̂́A��(
)�ɂȂ�̂́A��(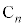 )���邢�͏�(
)���邢�͏�(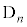 )�ɂ����āA�\���o��ꍇ�ł�(��̎��`�}�ŁA5��ڂ̗Θg�����Ă��������B�A���A4��ڂɂ͗Θg�͂���܂���)�B���̊m��
)�ɂ����āA�\���o��ꍇ�ł�(��̎��`�}�ŁA5��ڂ̗Θg�����Ă��������B�A���A4��ڂɂ͗Θg�͂���܂���)�B���̊m��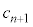 �́A
�́A 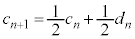 �@����F
�@����F�E��(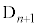 )�ɂȂ�̂́A��(
)�ɂȂ�̂́A��(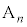 )�ɂ����ė����o�đ�A�Ƒ�B�������ɂȂ邩�A��(
)�ɂ����ė����o�đ�A�Ƒ�B�������ɂȂ邩�A��(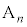 )�ő�A�Ƒ�B������ւ�����ꍇ�ɂ����ĕ\���o�đ�A�Ƒ�B�������ɂȂ�ꍇ�ł�(��̎��`�}�ŁA5��ڂ̃I�����W�F�̘g�����Ă�������)�B���̊m��
)�ő�A�Ƒ�B������ւ�����ꍇ�ɂ����ĕ\���o�đ�A�Ƒ�B�������ɂȂ�ꍇ�ł�(��̎��`�}�ŁA5��ڂ̃I�����W�F�̘g�����Ă�������)�B���̊m��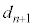 �́A
�́A 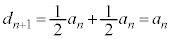 �@����G
�@����G�Ȃ��A��̎��`�}��4��ځA5��ڑ����ŁA���ΐF�̘g�͏�(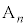 )�̑�A�Ƒ�B�����ւ����A���������ΐF�̘g�͏�(
)�̑�A�Ƒ�B�����ւ����A���������ΐF�̘g�͏�(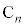 )�̑�A�Ƒ�B�����ւ�����\���Ă��܂��B4��ڑ����̎��`�}���A
)�̑�A�Ƒ�B�����ւ�����\���Ă��܂��B4��ڑ����̎��`�}���A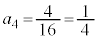 �C
�C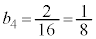 �C
�C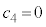 �C
�C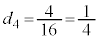
�E���A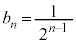 �@����H
�@����H
�����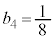 �����Ă��܂��B
�����Ă��܂��B
������D�ɑ�����āA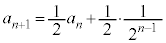
���ӂ�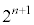 ��������(�Q�����̋Z�I���Q��)�A
��������(�Q�����̋Z�I���Q��)�A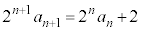
����āA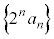 �́A�����F2�C�����F
�́A�����F2�C�����F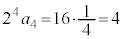 �����������ł��B
�����������ł��B 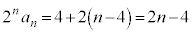 �@��
�@�� 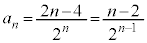 �@����I
�@����I����́A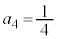 �����Ă��܂��B�܂��A�G���A
�����Ă��܂��B�܂��A�G���A 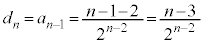 �@����J
�@����J����́A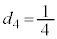 �����Ă��܂��B�J���F�ɑ�����āA
�����Ă��܂��B�J���F�ɑ�����āA ���ӂ�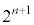 �������āA
�������āA 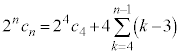 �@(
�@(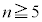 )
)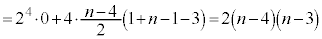 �@(�� ��������̌������g�p)
�@(�� ��������̌������g�p)�� 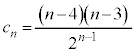 �@����K
�@����K 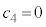 ���A
���A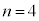 �̂Ƃ��������OK�ł��B
�̂Ƃ��������OK�ł��B
�ȏ���An���ɁA��A��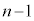 �ȏ�̋ʂ������Ă���m���́A�C�C�H�C�I���A
�ȏ�̋ʂ������Ă���m���́A�C�C�H�C�I���A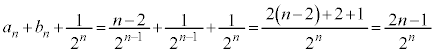 ......[�R]�@����L
......[�R]�@����L
��A��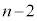 �ȏ�̋ʂ������Ă���m���̕��͒��ӂ��K�v�ł��B
�ȏ�̋ʂ������Ă���m���̕��͒��ӂ��K�v�ł��B
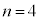 �̂Ƃ��A��A��2�ȏ�̋ʂ�����̂́A[�R]�̉�
�̂Ƃ��A��A��2�ȏ�̋ʂ�����̂́A[�R]�̉�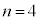 �Ƃ���
�Ƃ���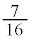 �ɁA(
�ɁA(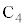 )�C(
)�C(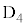 )�̏ꍇ�́A
)�̏ꍇ�́A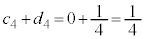 ��������
��������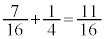 �ł͂���܂���B��̎��`�}������ƁA��A��2�A��B��3�����Ă���ꍇ(��B�̕�������)�̊m��
�ł͂���܂���B��̎��`�}������ƁA��A��2�A��B��3�����Ă���ꍇ(��B�̕�������)�̊m��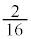 �������Ă��܂��B
�������Ă��܂��B
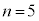 �̂Ƃ��ɂ��A��A��
�̂Ƃ��ɂ��A��A��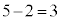 �A��B��4�̋ʂ������Ă���ꍇ(��B�̕�������)������܂��B
�A��B��4�̋ʂ������Ă���ꍇ(��B�̕�������)������܂��B
�܂�An���A��A��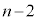 �̋ʂ������Ă���ꍇ�́A(
�̋ʂ������Ă���ꍇ�́A(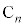 )�C(
)�C(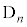 )�ɉ����āA��A��
)�ɉ����āA��A��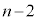 �A��B��
�A��B��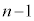 ����ꍇ��������K�v������܂��B����ȊO�ɁA��A��
����ꍇ��������K�v������܂��B����ȊO�ɁA��A��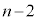 ���邱�Ƃ͂���܂���B
���邱�Ƃ͂���܂���B
��A��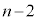 �A��B��
�A��B��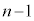 ����̂́A
����̂́A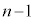 ���ɁA��A��B�Ƃ���
���ɁA��A��B�Ƃ���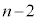 �ʂ������Ă���(��
�ʂ������Ă���(��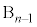 )�A�����o���ꍇ�����ł��B���̊m���́A
)�A�����o���ꍇ�����ł��B���̊m���́A 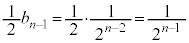 �@����M
�@����M����āAn���ɑ�A��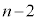 �ȏ�ʂ������Ă���m���́A�J�C�K�C�L�C�M���A
�ȏ�ʂ������Ă���m���́A�J�C�K�C�L�C�M���A 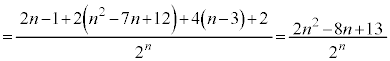 ......[�T]
......[�T]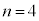 �̂Ƃ�
�̂Ƃ�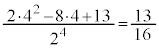 �C
�C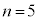 �̂Ƃ�
�̂Ƃ�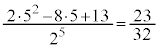 �ƂȂ�܂����A�㑤�̑J�ڐ}�Ő����ċ��߂���m���Ɉ�v���܂��B
�ƂȂ�܂����A�㑤�̑J�ڐ}�Ő����ċ��߂���m���Ɉ�v���܂��B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@�c�嗝�H���wTOP�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B 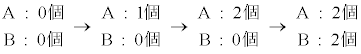
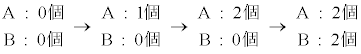
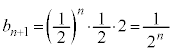 �@����E
�@����E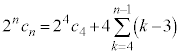 �@(
�@(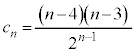 �@����K
�@����K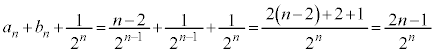 ......[�R]�@����L
......[�R]�@����L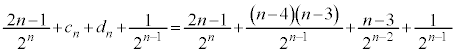
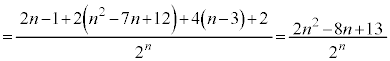 ......[�T]
......[�T]