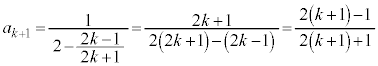�Q�����̋Z�I�@�@�@�֘A���
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���̍��ڂ́A2���ԑQ�����A3���ԑQ�������Q�Ƃ��Ă��������B
(1) 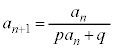 �^�C�v�F���ӂ̋t�����l���A
�^�C�v�F���ӂ̋t�����l���A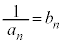 �Ƃ����B
�Ƃ����B (2) 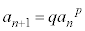 (
(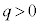 �C
�C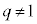 )�^�C�v�F���ӂ̑ΐ����l���A
)�^�C�v�F���ӂ̑ΐ����l���A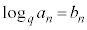 �Ƃ����B
�Ƃ����B (3) 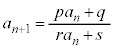 (
(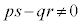 �C
�C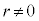 )�F
)�F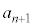 ��
��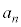 ��x�Œu��������2���������̉���α�Cβ �Ƃ��āA
��x�Œu��������2���������̉���α�Cβ �Ƃ��āA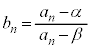 �Ƃ����B
�Ƃ����B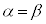 �̏ꍇ��
�̏ꍇ��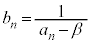 �Ƃ����B
�Ƃ����B
��1�@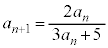 �C
�C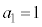
���@(1) �̃^�C�v�ł��B�Q�������ӂ̋t�����l����ƁA
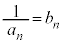 �Ƃ����ƁA
�Ƃ����ƁA
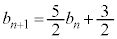 �@����@
�@����@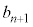 ��
��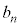 ��α�Ƃ����ƁA
��α�Ƃ����ƁA
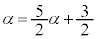 �@����A
�@����A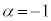
�@�|�A���A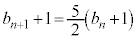
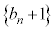 �́A����
�́A����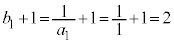 �C����
�C����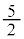 �����䐔���B
�����䐔���B
�� 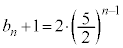
�� 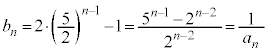
�� 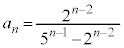 ......[��]
......[��]
��2�@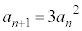 �C
�C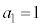
���@(2) �̃^�C�v�ł��B�Q�������ӂ��ΐ����l����ƁA���3�Ƃ��āA
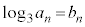 �Ƃ����ƁA
�Ƃ����ƁA
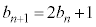 �@����@
�@����@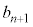 ��
��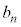 ��α�Ƃ����ƁA
��α�Ƃ����ƁA
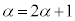 �@����A
�@����A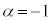
�@�|�A���A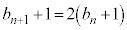
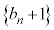 �́A����
�́A����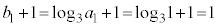 �C����2�����䐔���B
�C����2�����䐔���B
�� 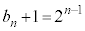
�� 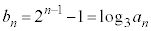
�� 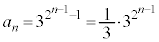 ......[��]
......[��]
��3�@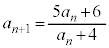 �C
�C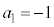
���@(3)��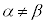 �ƂȂ�^�C�v�ł��B
�ƂȂ�^�C�v�ł��B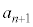 ��
��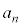 ��x�Œu��������ƁA
��x�Œu��������ƁA
������Đ�������ƁA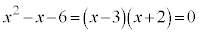
�� 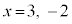
���̉���p���āA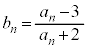 (����A���q�͓���ւ���Ă�OK�ł�)�Ƃ����ƁA
(����A���q�͓���ւ���Ă�OK�ł�)�Ƃ����ƁA
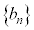 �́A����
�́A����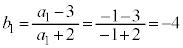 �C����
�C����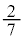 �����䐔��(�K���A���䐔��ɂȂ�܂�)�B
�����䐔��(�K���A���䐔��ɂȂ�܂�)�B
�� 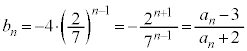
������āA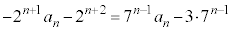
�� 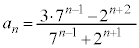 ......[��]
......[��]
��4�@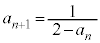 �C
�C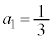
���@(3)��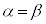 �ƂȂ�^�C�v�ł��B
�ƂȂ�^�C�v�ł��B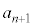 ��
��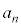 ��x�Œu��������ƁA
��x�Œu��������ƁA
������Đ�������ƁA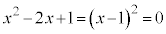
�� 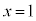
�d���ɂȂ��Ă��܂��Ƃ��ɂ́A��3�̂悤�ɂ͂ł��܂���B�o�Ă����d����p���āA����ɁA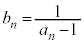 �Ƃ����܂��B
�Ƃ����܂��B
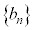 �́A����
�́A����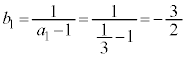 �C����
�C����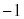 ����������(�K���A��������ɂȂ�܂�)�B
����������(�K���A��������ɂȂ�܂�)�B
�� 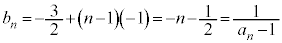
������āA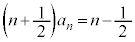
�� 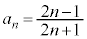 ......[��]�@(��6���Q�Ƃ��Ă�������)
......[��]�@(��6���Q�Ƃ��Ă�������)
��5�@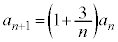 �C
�C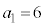
���@(4)�̃^�C�v�ł��B
�̕���A���q�ɁA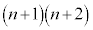 �������܂�(����������̂��A��������̂��́A���̌`�ł��낢��ł�)�B
�������܂�(����������̂��A��������̂��́A���̌`�ł��낢��ł�)�B
�� 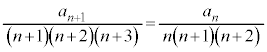
����́A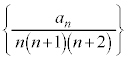 ���萔�l���Ƃ鐔��ł��邱�Ƃ��Ӗ����Ă��܂��B����
���萔�l���Ƃ鐔��ł��邱�Ƃ��Ӗ����Ă��܂��B����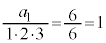 ���A
���A
�� 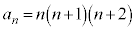 ......[��]
......[��]
��6�@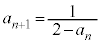 �C
�C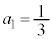
���@��4�ɂ��ẮA�����킵���Z�I���g�������A�\���������w�I�A�[�@�ŏؖ����Ă��܂������ȒP�ł��B
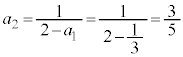 �C
�C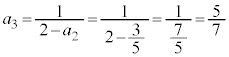 �C
�C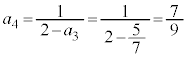 �C��� ���A
�C��� ���A
�Ɨ\���ł��܂��B
(�T) 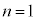 �̂Ƃ��A
�̂Ƃ��A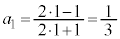 ���\���͐��藧���܂��B
���\���͐��藧���܂��B
(�U) 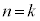 �̂Ƃ��A�\�������藧�Ƃ���ƁA
�̂Ƃ��A�\�������藧�Ƃ���ƁA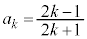
�^�Q�������A
����āA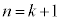 �̂Ƃ����\���͐������܂��B
�̂Ƃ����\���͐������܂��B
(�T)�C(�U)���A�\���́A���ׂĂ̎��R��n�ɂ��Đ��藧���A
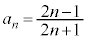 ......[��]
......[��]
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���w��b����TOP�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B 
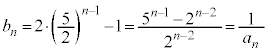
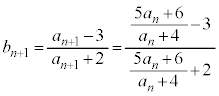
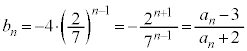
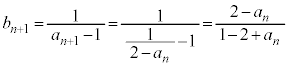
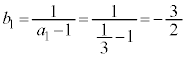 �C����
�C����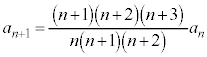
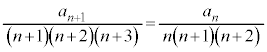
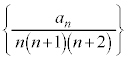 ���萔�l���Ƃ鐔��ł��邱�Ƃ��Ӗ����Ă��܂��B����
���萔�l���Ƃ鐔��ł��邱�Ƃ��Ӗ����Ă��܂��B����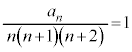
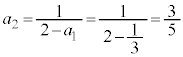 �C
�C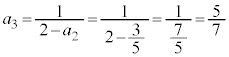 �C
�C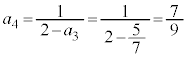 �C��� ���A
�C��� ���A