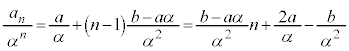3項間漸化式 関連問題
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
数列の隣接3項: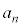 ,
,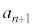 ,
,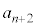 に関する関係式を3項間漸化式と言います。
に関する関係式を3項間漸化式と言います。
基本形: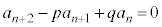 ・・・①,
・・・①,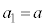 ,
,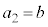 ,
,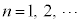
まず、等比数列の漸化式の形を作ることを考えます。
数列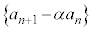 が、公比:β の等比数列だとすると、
が、公比:β の等比数列だとすると、
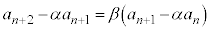 ・・・②
・・・②
展開して整理すると、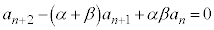
①と比べると、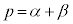 ,
,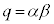
これより、α,β は2次方程式: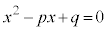 ・・・③ の2解です。
・・・③ の2解です。
2次方程式③を3項間漸化式①の特性方程式と言います。与えられた3項間漸化式①の各項の係数を用いて作った2次方程式です。
特性方程式③の解α,β を求めて、②の形を作ります。
1) ③が相異なる2実数解をもつ場合(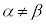 )には、
)には、
数列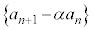 は、初項:
は、初項: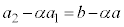 ,公比:β の等比数列ゆえ、
,公比:β の等比数列ゆえ、
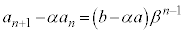 ・・・④
・・・④
このとき、①を、
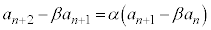
と書き直すこともできます。
これより、数列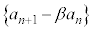 は、初項:
は、初項: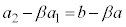 ,公比:αの等比数列となるので、
,公比:αの等比数列となるので、
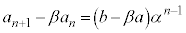 ・・・⑤
・・・⑤
④-⑤より、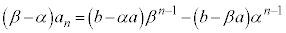
∴ 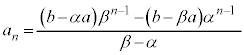
[注意] 結果を暗記しても何の意味もありません。手順を覚えること。
2) ③が重解αをもつ場合( )には、②は、
)には、②は、
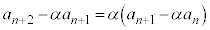
となり、数列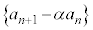 は、初項:
は、初項: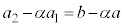 ,公比:αの等比数列となり、
,公比:αの等比数列となり、
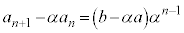
両辺を で割ると、
で割ると、
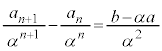
数列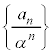 は、初項:
は、初項: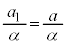 ,公差:
,公差: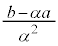 の等差数列ゆえ、
の等差数列ゆえ、
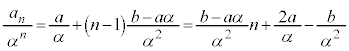
∴ 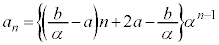
この場合には、等比数列を2通り作ることができないので、1)の手順では一般項が求められません。
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
数学基礎事項TOP 数学TOP TOPページに戻る
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
各問題の著作権は
出題大学に属します。©2005-2024(有)りるらる 苦学楽学塾 随時入会受付中!理系大学受験ネット塾苦学楽学塾(ご案内はこちら)ご入会は、
まず、こちらまでメールを
お送りください。 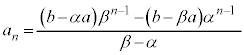
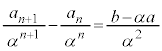
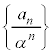 は、初項:
は、初項: