�c�嗝�H���w'23�N[4]
(1) 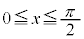 �ɂ����ď�ɕs����
�ɂ����ď�ɕs����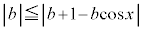 �����藧�悤�Ȏ���b�̒l�͈̔͂�
�����藧�悤�Ȏ���b�̒l�͈̔͂�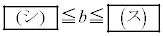 �ł���B
�ł���B
�ȉ��Ab��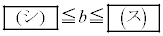 ����0�łȂ������Ƃ��A����
����0�łȂ������Ƃ��A����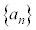 ���A
���A
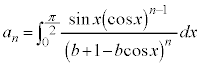 �@(
�@(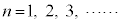 )
)
(2) 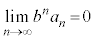 �����藧���Ƃ��ؖ����Ȃ����B
�����藧���Ƃ��ؖ����Ȃ����B
(3) 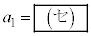 �ł���B
�ł���B
(4) 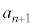 ��
��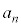 �Cn�Cb��p���ĕ\���ƁA
�Cn�Cb��p���ĕ\���ƁA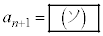 �ƂȂ�B
�ƂȂ�B
(5) 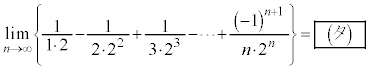 �ł���B
�ł���B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@(4)���Q���������̂ŁA���R�����ϕ��ɂȂ�܂����A������ƈ��������邩���m��܂���B
(1) b�����ӂɕʂ�Ă��Ă͂��ɂ����̂ŁA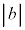 �Ŋ����āA1�����ɂ��܂��B
�Ŋ����āA1�����ɂ��܂��B 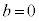 �̂Ƃ��A�^�s�����́A
�̂Ƃ��A�^�s�����́A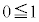 �ƂȂ�A��ɐ������܂��B
�ƂȂ�A��ɐ������܂��B
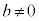 �̂Ƃ��A�^�s�������ӂ�
�̂Ƃ��A�^�s�������ӂ�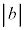 �Ŋ���ƁA
�Ŋ���ƁA�@���A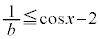
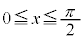 �ɂ�����
�ɂ�����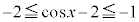 ���A���ꂪ��ɐ������邽�߂ɂ́A
���A���ꂪ��ɐ������邽�߂ɂ́A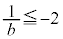 �C�܂�A
�C�܂�A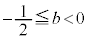 �@����B
�@����B
�A���A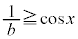
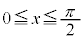 �ɂ�����
�ɂ�����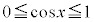 ���A���ꂪ��ɐ������邽�߂ɂ́A
���A���ꂪ��ɐ������邽�߂ɂ́A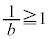 �C�܂�A
�C�܂�A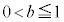 �@����C
�@����C
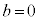 �ƇB�C�C���A
�ƇB�C�C���A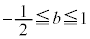 �@
�@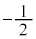 ......[�V]�C1 ......[�X]
......[�V]�C1 ......[�X]
(2) 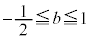 ����
����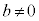 �̂Ƃ��A
�̂Ƃ��A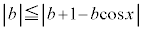 ����ɐ�������̂ŁA
����ɐ�������̂ŁA 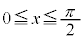 �ɂ����āA
�ɂ����āA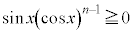 ���A
���A���̍��ӂƉE�ӂ́A
���A�D�́A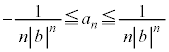
����āA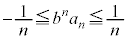 �@����E
�@����E
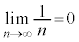 �C�͂��݂����̌������A
�C�͂��݂����̌������A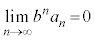
�ȏ���A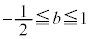 ����
����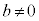 �̂Ƃ��A
�̂Ƃ��A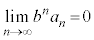 �ł��B(�ؖ��I)
�ł��B(�ؖ��I)
(3) 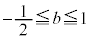 ����
����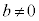 �̂Ƃ��A
�̂Ƃ��A 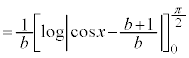
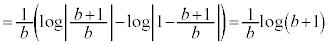 ......[�Z]
......[�Z]���D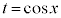 �Ƃ������u���ϕ�����ƁA
�Ƃ������u���ϕ�����ƁA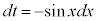 �Cx�F
�Cx�F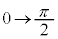 �̂Ƃ�t �F
�̂Ƃ�t �F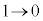 ���A
���A �ƂȂ�̂ł����A(2)�C(3)�̒�ϕ��ɂ����ẮAt �����̂܂�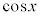 �Ə����Ă��܂��B
�Ə����Ă��܂��B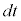 ��
��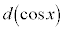 �Ə����܂��B���������ƁA��ϕ��̏�[�Ɖ��[��
�Ə����܂��B���������ƁA��ϕ��̏�[�Ɖ��[��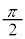 ��0�̂܂܂ł悢���ƂɂȂ�܂��B
��0�̂܂܂ł悢���ƂɂȂ�܂��B
�ƌ��āA
�Ƃ���Ɣj�]���܂��B
����ŁA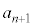 ���ϕ���p����
���ϕ���p����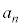 �ŕ\�����A�Ƃ����ŏ��̎v�f�Ƃ͈قȂ�܂����A���ԍ���1���点�āA
�ŕ\�����A�Ƃ����ŏ��̎v�f�Ƃ͈قȂ�܂����A���ԍ���1���点�āA 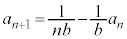 ......[�\]�@����F
......[�\]�@����F
(5) (2)�𗘗p����̂��낤�A�Ƃ������ƂŁA(4)�ŋ��߂��Q������p���āA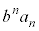 ���ǂ��Ȃ邩�ׂĂ݂܂��B�F�̗��ӂ�
���ǂ��Ȃ邩�ׂĂ݂܂��B�F�̗��ӂ�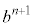 �������āA
�������āA 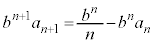 �@����G
�@����G���������ނ��߂ɁA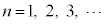 �Ƃ��Ă݂܂��B
�Ƃ��Ă݂܂��B 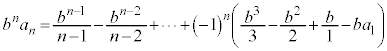 �@���(��)�@�Ɖ��肷��ƁA�G��p���āA
�@���(��)�@�Ɖ��肷��ƁA�G��p���āA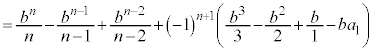 �@����H
�@����H����āA���w�I�A�[�@���A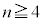 �ƂȂ鎩�R��n�ɑ��āA(��)���������܂��B�H�̗��ӂ�
�ƂȂ鎩�R��n�ɑ��āA(��)���������܂��B�H�̗��ӂ�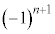 ��������ƁA
��������ƁA 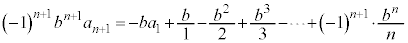
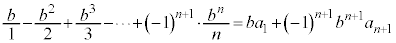 �@����I
�@����I ����
����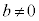 �̂Ƃ��A�E���A
�̂Ƃ��A�E���A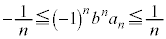 �C�����ŁA
�C�����ŁA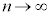 �Ƃ���ƁA
�Ƃ���ƁA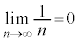 ���A
���A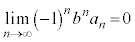 �@(�͂��݂����̌������Q��)���̂Ƃ��A�I��
�@(�͂��݂����̌������Q��)���̂Ƃ��A�I��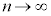 �Ƃ���ƁA�E�Ӂ�
�Ƃ���ƁA�E�Ӂ�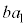
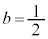 ��
��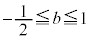 �����̂ŁA�I��
�����̂ŁA�I��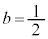 �Ƃ��āA
�Ƃ��āA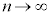 �Ƃ���ƁA[�Z]���A
�Ƃ���ƁA[�Z]���A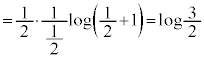 ......[�^]
......[�^]
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@�c�嗝�H���wTOP�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B 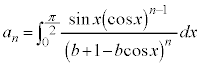 �@(
�@(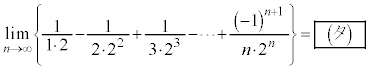 �ł���B
�ł���B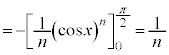
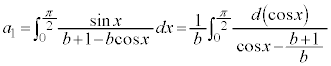
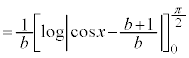
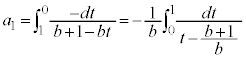
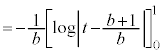
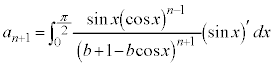
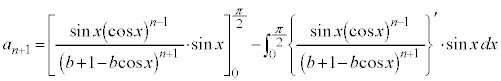
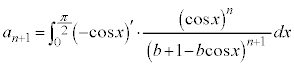
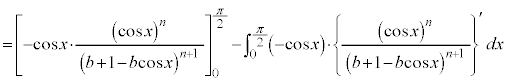
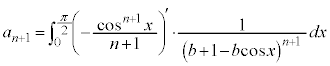
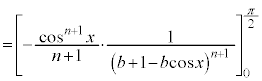
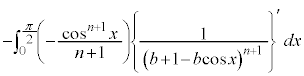
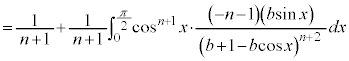
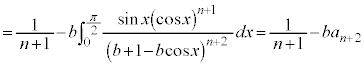
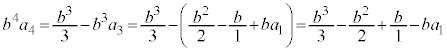
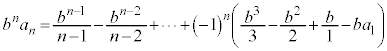 �@���(��)�@�Ɖ��肷��ƁA�G��p���āA
�@���(��)�@�Ɖ��肷��ƁA�G��p���āA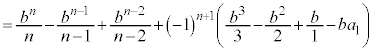 �@����H
�@����H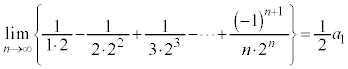
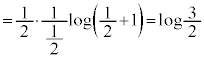 ......[�^]
......[�^]