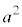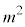�c�嗝�H���w'25�N[5]
���W���ʏ��3�_A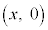 �CB
�CB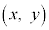 �CC
�CC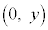 ���Ƃ�B�������AB�͒P�ʉ~������A
���Ƃ�B�������AB�͒P�ʉ~������A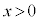 �C
�C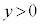 �ł���B���̂Ƃ��A����AB��BC�̒������������Ȃ�x�̒l��
�ł���B���̂Ƃ��A����AB��BC�̒������������Ȃ�x�̒l�� �ł���B
�ł���B
���ɁAn��2�ȏ�̐����Ƃ��A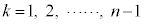 �ɑ���
�ɑ���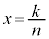 �̂Ƃ��̐���AB��BC�̒Z�����̒�����
�̂Ƃ��̐���AB��BC�̒Z�����̒�����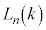 �ƕ\���B
�ƕ\���B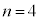 �Ƃ���ƁA
�Ƃ���ƁA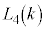
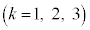 �̍ő�l��
�̍ő�l��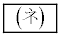 �ł���B����A
�ł���B����A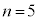 �̂Ƃ�
�̂Ƃ�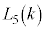 ���ő�ƂȂ�k�̒l��
���ő�ƂȂ�k�̒l�� ��
�� ��2����B���l�ɁA2�ȏ�̐���a�ŁA
��2����B���l�ɁA2�ȏ�̐���a�ŁA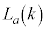 ���ő�ƂȂ�k�̒l��2������̂��l���A���̂悤��k�̂����傫�����̒l��m�Ƃ����B���̂Ƃ��Am��a�̎��ŕ\����
���ő�ƂȂ�k�̒l��2������̂��l���A���̂悤��k�̂����傫�����̒l��m�Ƃ����B���̂Ƃ��Am��a�̎��ŕ\����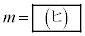 �ƂȂ�B�܂��A
�ƂȂ�B�܂��A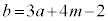 �Ƃ������Ƃ��A
�Ƃ������Ƃ��A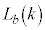 ���ő�ƂȂ�k�̒l��2����A�����̑傫������a��m��1�����ŕ\����
���ő�ƂȂ�k�̒l��2����A�����̑傫������a��m��1�����ŕ\���� �ƂȂ�B
�ƂȂ�B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@��̓I�ɍl�������悤�A�Ƃ����o��҂̐e�S����������ł����A�Ō��[�t]�͓��ł��B
B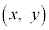 ���P�ʉ~������̂ŁA
���P�ʉ~������̂ŁA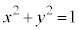 �@����@
�@����@ A��x����̓_�AC��y����̓_�ŁA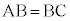 �̂Ƃ��A
�̂Ƃ��A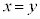 ���A
���A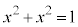 �@��
�@�� 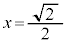 ......[�k]
......[�k]
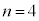 �̂Ƃ��A
�̂Ƃ��A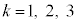 �Ƃ���
�Ƃ���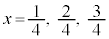
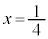 �̂Ƃ�(
�̂Ƃ�(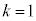 )�A�@��
)�A�@��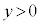 ���
���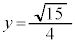 �C
�C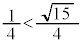 ���A
���A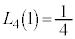
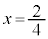 �̂Ƃ�(
�̂Ƃ�(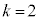 )�A�@��
)�A�@��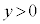 ���
���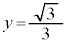 �C
�C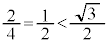 ���A
���A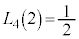
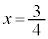 �̂Ƃ�(
�̂Ƃ�(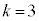 )�A�@��
)�A�@��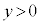 ���
���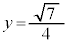 �C
�C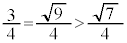 ���A
���A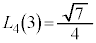
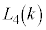 (
(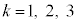 )�̍ő�l��
)�̍ő�l��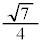 ......[�l]
......[�l]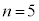 �̂Ƃ��A
�̂Ƃ��A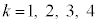 �Ƃ���
�Ƃ���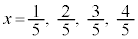
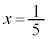 �̂Ƃ�(
�̂Ƃ�(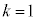 )�A�@��
)�A�@��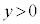 ���
���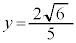 �C
�C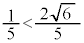 ���A
���A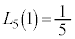
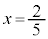 �̂Ƃ�(
�̂Ƃ�(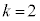 )�A�@��
)�A�@��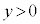 ���
���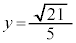 �C
�C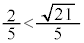 ���A
���A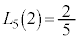
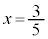 �̂Ƃ�(
�̂Ƃ�(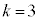 )�A�@��
)�A�@��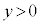 ���
���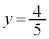 �C
�C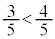 ���A
���A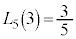
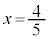 �̂Ƃ�(
�̂Ƃ�(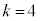 )�A�@��
)�A�@��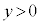 ���
���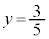 �C
�C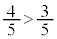 ���A
���A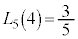
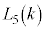 (
(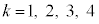 )���ő�Ƃ���k�̒l�́A3 ......[�m]�C4 ......[�n]
)���ő�Ƃ���k�̒l�́A3 ......[�m]�C4 ......[�n]
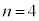 �C
�C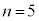 �ŁAk���傫���Ȃ�Ƃ�
�ŁAk���傫���Ȃ�Ƃ�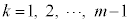 �͑傫���Ȃ�
�͑傫���Ȃ�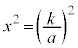 �͏������Ȃ�܂��B
�͏������Ȃ�܂��B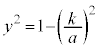 �̂Ƃ��A
�̂Ƃ��A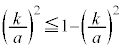 ���A
���A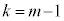
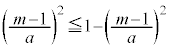 �̂Ƃ��A
�̂Ƃ��A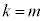 �C
�C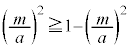 �̂Ƃ��A
�̂Ƃ��A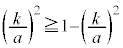
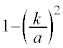 �ł����āA
�ł����āA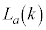 ���ő�̂Ƃ���k��
���ő�̂Ƃ���k��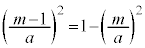 �Ƃ���ƁA
�Ƃ���ƁA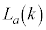 ��
��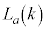 ���������̂����ő�̂��̂ł��B
���������̂����ő�̂��̂ł��B
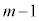 �ł����āA
�ł����āA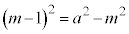 ���ő�̂Ƃ���k��
���ő�̂Ƃ���k��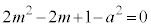 �Ƃ���ƁA
�Ƃ���ƁA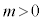 ��
��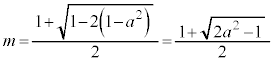 ���������̂����ŏ��̂��̂ł��B
���������̂����ŏ��̂��̂ł��B
�܂�A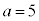 ���ő�ƂȂ�k�̒l��
���ő�ƂȂ�k�̒l��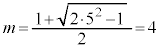 �C
�C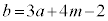 ��2�ł���Ƃ��A
��2�ł���Ƃ��A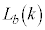 �ł����āA
�ł����āA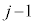 �C
�C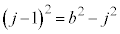 �͘A��2�����ł����āA
�͘A��2�����ł����āA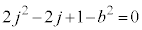 �Ƃ���ƁA
�Ƃ���ƁA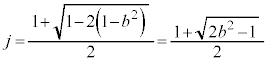 �ł��B
�ł��B
����āA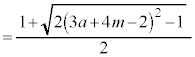
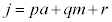 �@����A
�@����A
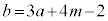 �@����B
�@����B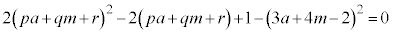 ���A
���A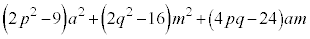 ......[�q]
......[�q]
���D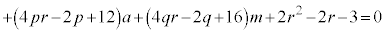 �̂Ƃ�
�̂Ƃ�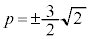 �ƂȂ�A[�n]�̌��ʂ������܂��B
�ƂȂ�A[�n]�̌��ʂ������܂��B
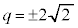 �Ƃ��āA
�Ƃ��āA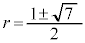 ���ő�Ƃ���k�̒l��2��(�傫������j�Ƃ���Ƒ�����
���ő�Ƃ���k�̒l��2��(�傫������j�Ƃ���Ƒ�����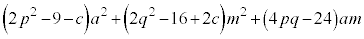 �ł��Bj�͎��R���ł�)����Ƃ������Ƃ́A�A�ƑS�����l�ɍl���āA
�ł��Bj�͎��R���ł�)����Ƃ������Ƃ́A�A�ƑS�����l�ɍl���āA
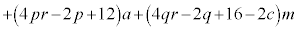 �@����C
�@����C
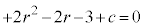 �@����D
�@����D
�Ƃ��Ă��Aj��a��m��1�����̌`�ɕ\�����Ƃ��ł��܂���B
�����ŁAj��a��m��1�����F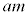 (p�Cq�Cr�͎����̒萔)�ŕ\���A
(p�Cq�Cr�͎����̒萔)�ŕ\���A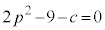 �ƂƂ��ɁA�D�ɑ�����Ă݂܂��B
�ƂƂ��ɁA�D�ɑ�����Ă݂܂��B
��������ƁA
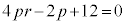 �@����E
�@����E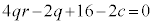 �C
�C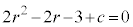 �C
�C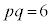 �ƂȂ�Aj�������ɂȂ�܂���B�����ŁA�B���������A�B�̒萔c�{���E�ɉ����čl���܂��B
�ƂȂ�Aj�������ɂȂ�܂���B�����ŁA�B���������A�B�̒萔c�{���E�ɉ����čl���܂��B
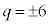
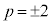 �@����F
�@����F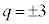 �C
�C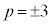 �C
�C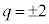 �Ca�Cm�̌W����0�Ƃ����(�P�������Q��)�A
�Ca�Cm�̌W����0�Ƃ����(�P�������Q��)�A
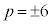 �@����G
�@����G
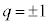 �@����H
�@����H
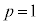 �@����I
�@����I
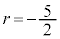 �@����J
�@����J
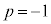 �@����K
�@����K
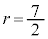 �@����L
�@����L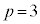 �Cj�𐮐��Ƃ��邽�߂ɁAp�Cq�𐮐��Ƃ���ƁA
�Cj�𐮐��Ƃ��邽�߂ɁAp�Cq�𐮐��Ƃ���ƁA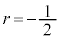 �C
�C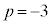 (��������)�C�܂��́A
(��������)�C�܂��́A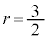 �C
�C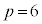 (��������)�C�܂��́A
(��������)�C�܂��́A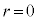 �C
�C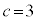 (��������)�C�܂��́A
(��������)�C�܂��́A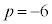 �C
�C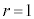 (��������)
(��������)
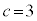 �̂Ƃ��J���
�̂Ƃ��J���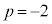 �C
�C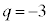 �̂Ƃ��J���
�̂Ƃ��J���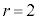 �C�������j�������ɂȂ炸�s�K�B
�C�������j�������ɂȂ炸�s�K�B
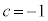 �̂Ƃ��J���
�̂Ƃ��J���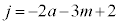 �C
�C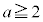 �̂Ƃ��J���
�̂Ƃ��J���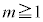 �C�������j�������ɂȂ炸�s�K�B
�C�������j�������ɂȂ炸�s�K�B
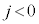 �̂Ƃ��J���
�̂Ƃ��J���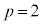 �C�L���
�C�L���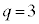 �C�G�����������s�K�B
�C�G�����������s�K�B
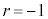 �̂Ƃ��J���
�̂Ƃ��J���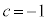 �C�L���
�C�L���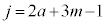 �C�G�����������s�K�B
�C�G�����������s�K�B
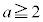 �C
�C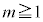 �̂Ƃ��I���
�̂Ƃ��I���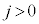 �C�G�C�H�C�K���
�C�G�C�H�C�K���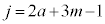 �C�L���������܂����A
�C�L���������܂����A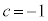 �́A
�́A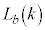 �C
�C �ł�
�ł� �ƂȂ��Ă��܂����ߕs�K�B
�ƂȂ��Ă��܂����ߕs�K�B
 �C
�C �̂Ƃ��J���
�̂Ƃ��J��� �C�G�C�H�C�K���
�C�G�C�H�C�K��� �C�L���������܂��B���̂Ƃ��A
�C�L���������܂��B���̂Ƃ��A �́A
�́A �C
�C �̂Ƃ�
�̂Ƃ� �ł��B����āA
�ł��B����āA
�Ɍ����܂��B�t�ɁA[�t]���A���� �ł���·F��
�ł���·F�� �C
�C �C
�C �Ca�Cm�̌W����0�ŁA�F����
�Ca�Cm�̌W����0�ŁA�F���� �������ƇE�ƂȂ�A�C���������A
�������ƇE�ƂȂ�A�C���������A ���ő�Ƃ���k�̒l�̂����傫������j�ɂȂ�܂��B
���ő�Ƃ���k�̒l�̂����傫������j�ɂȂ�܂��B
 ......[�t]
......[�t]
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@�c�嗝�H���wTOP�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B�Ȃ��A�́A
��w�y�w�m����ł��B©2005-2025(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B 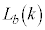 �ł����āA
�ł����āA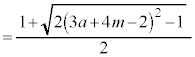
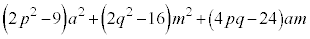 ......[�q]
......[�q]