慶應大学理工学部2025年数学入試問題
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
[1](1) 複素数平面上で、方程式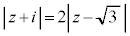 を満たす点z全体が表す図形は、中心が
を満たす点z全体が表す図形は、中心が ,半径が
,半径が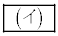 の円である。
の円である。 (2) nを自然数とする。1からnまでの自然数の中で6または8または9で割り切れるものの個数を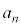 で表す。このとき
で表す。このとき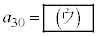 となる。また、
となる。また、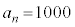 を満たす最大のnは
を満たす最大のnは である。
である。 (3) 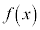 を微分可能な関数とし、
を微分可能な関数とし、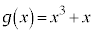 とする。関数
とする。関数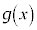 は微分可能な逆関数
は微分可能な逆関数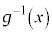 をもつ。定数t に対して、関数
をもつ。定数t に対して、関数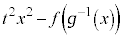 は
は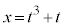 で極値をとるとする。このとき、
で極値をとるとする。このとき、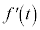 をt の多項式で表すと
をt の多項式で表すと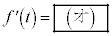 となる。次に、任意の定数t に対して、関数
となる。次に、任意の定数t に対して、関数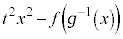 は
は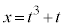 で極値をとるとする。このとき、
で極値をとるとする。このとき、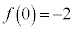 ならば、
ならば、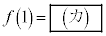 である。
である。 [解答へ]
[2] 座標平面上の点P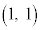 と点Q
と点Q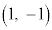 および曲線
および曲線
C: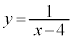 (
(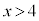 )
) を考える。
(1) 曲線Cの接線で点Qを通るものは存在しないことを証明しなさい。
(2) 曲線Cの接線で点Pを通るものをlとし、Cとlの接点をAとする。このとき、lの方程式は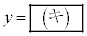 であり、点Aの座標は
であり、点Aの座標は である。また、曲線C上の点Bが
である。また、曲線C上の点Bが を満たすとき、点Bの座標は である。
である。 (3) A,Bを(2)で定めた点とする。正の数t に対し、曲線上の点R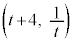 は点Aと異なるものとする。線分ARを2:1に内分する点をSとし、線分BSを3:2に内分する点をT
は点Aと異なるものとする。線分ARを2:1に内分する点をSとし、線分BSを3:2に内分する点をT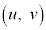 とするとき、uをt の式で表すと
とするとき、uをt の式で表すと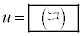 である。また、
である。また、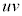 の値は
の値は のとき最小となる。
のとき最小となる。 [解答へ]
[3] 点P,Qを数直線の原点におき、1個のさいころを投げて出た目に応じてP,Qを動かす。偶数の目が出たときはPを正の向きに1だけ動かし、5または6の目が出たときはQを正の向きに1だけ動かす。たとえば、6の目が出たときはP,Qをともに正の方向に1だけ動かす。PとQの距離が初めて2となるまでさいころを投げ続けることとし、PとQの距離が2となったら、それ以降はさいころを投げない。n回さいころを投げてPとQの距離が2となる確率を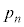 とする。
とする。
(1) 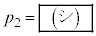 である。
である。 (2) n回さいころを投げて、PがQよりも正の向きに1だけ進んでいる確率を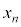 ,PとQが同じ位置にある確率を
,PとQが同じ位置にある確率を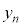 ,QがPよりも正の向きに1だけ進んでいる確率を
,QがPよりも正の向きに1だけ進んでいる確率を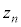 とすると
とすると という関係式が成立する。また、 が成り立つ。ただし、
が成り立つ。ただし、 〜
〜 には数を記入すること。
には数を記入すること。 (3) 関係式
(4) 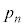 をnを用いて表すと
をnを用いて表すと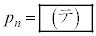 となる。
となる。 [解答へ]
[4] 以下の設問では、区間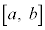 で連続な関数
で連続な関数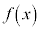 ,
,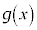 ,
,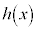 に対して、区間
に対して、区間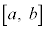 で
で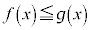 ならば
ならば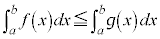 であること、および
であること、および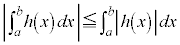 であることをことわりなしに用いてよい。
であることをことわりなしに用いてよい。
(1) 自然数nに対して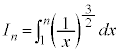 とする。このとき、
とする。このとき、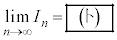 である。
である。 (2) 自然数nに対して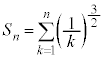 とする。すべてのnに対して不等式
とする。すべてのnに対して不等式 を証明しなさい。
(3) 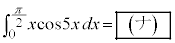 である。
である。 (4) kを自然数とするとき、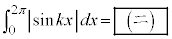 である。
である。 (5) 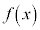 を微分可能な関数とし、Mを正の定数とする。区間
を微分可能な関数とし、Mを正の定数とする。区間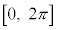 で、
で、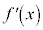 は連続かつ
は連続かつ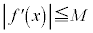 と仮定する。自然数k,nに対して、
と仮定する。自然数k,nに対して、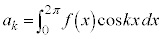 とし、
とし、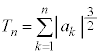 とする。このとき、すべてのnに対して不等式
とする。このとき、すべてのnに対して不等式 を証明しなさい。ただし、必要であれば(2)の不等式と(4)の等式を証明なしに用いてよい。
[解答へ]
[5] 座標平面上に3点A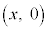 ,B
,B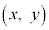 ,C
,C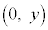 をとる。ただし、Bは単位円周上を動き、
をとる。ただし、Bは単位円周上を動き、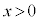 ,
,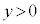 である。このとき、線分ABとBCの長さが等しくなるxの値は
である。このとき、線分ABとBCの長さが等しくなるxの値は である。
である。
次に、nを2以上の整数とし、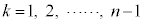 に対して
に対して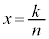 のときの線分ABとBCの短い方の長さを
のときの線分ABとBCの短い方の長さを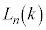 と表す。
と表す。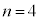 とすると、
とすると、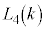
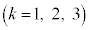 の最大値は
の最大値は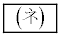 である。一方、
である。一方、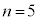 のとき
のとき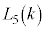 が最大となるkの値は
が最大となるkの値は と
と の2個ある。同様に、2以上の整数aで、
の2個ある。同様に、2以上の整数aで、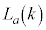 が最大となるkの値が2個あるものを考え、そのようなkのうち大きい方の値をmとおく。このとき、mをaの式で表すと
が最大となるkの値が2個あるものを考え、そのようなkのうち大きい方の値をmとおく。このとき、mをaの式で表すと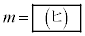 となる。また、
となる。また、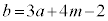 とおいたとき、
とおいたとき、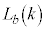 が最大となるkの値も2個あり、それらの大きい方をaとmの1次式で表すと
が最大となるkの値も2個あり、それらの大きい方をaとmの1次式で表すと となる。
となる。
[解答へ]
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
慶大理工数学TOP 数学TOP TOPページに戻る
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
各問題の著作権は
出題大学に属します。©2005-2025(有)りるらる 苦学楽学塾 随時入会受付中!理系大学受験ネット塾苦学楽学塾(ご案内はこちら)ご入会は、
まず、こちらまでメールを
お送りください。 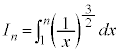 とする。このとき、
とする。このとき、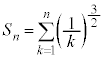 とする。すべてのnに対して不等式
とする。すべてのnに対して不等式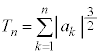 とする。このとき、すべてのnに対して不等式
とする。このとき、すべてのnに対して不等式