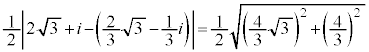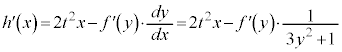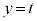�c�嗝�H���w'25�N[1]
(1) ���f�����ʏ�ŁA������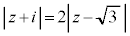 �����_z�S�̂��\���}�`�́A���S��
�����_z�S�̂��\���}�`�́A���S�� �C���a��
�C���a��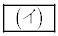 �̉~�ł���B
�̉~�ł���B (2) n�����R���Ƃ���B1����n�܂ł̎��R���̒���6�܂���8�܂���9�Ŋ�������̂̌���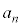 �ŕ\���B���̂Ƃ�
�ŕ\���B���̂Ƃ�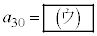 �ƂȂ�B�܂��A
�ƂȂ�B�܂��A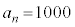 �����ő��n��
�����ő��n�� �ł���B
�ł���B (3) 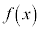 ������\�Ȋ��Ƃ��A
������\�Ȋ��Ƃ��A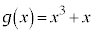 �Ƃ���B��
�Ƃ���B��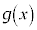 �͔����\�ȋt��
�͔����\�ȋt��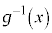 �����B�萔t �ɑ��āA��
�����B�萔t �ɑ��āA��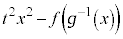 ��
��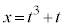 �ŋɒl���Ƃ�Ƃ���B���̂Ƃ��A
�ŋɒl���Ƃ�Ƃ���B���̂Ƃ��A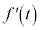 ��t �̑������ŕ\����
��t �̑������ŕ\����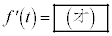 �ƂȂ�B���ɁA�C�ӂ̒萔t �ɑ��āA��
�ƂȂ�B���ɁA�C�ӂ̒萔t �ɑ��āA��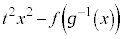 ��
��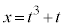 �ŋɒl���Ƃ�Ƃ���B���̂Ƃ��A
�ŋɒl���Ƃ�Ƃ���B���̂Ƃ��A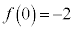 �Ȃ�A
�Ȃ�A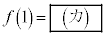 �ł���B
�ł���B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@(1)�̓A�|���j�E�X�̉~�ł��B(2)�́A�ȉ��ł͂��ǂ��Ǐ����܂������������ł͂�����ƌv�Z���܂��傤�B(3)�̋t���̖��͍������Ղ��ł����A��b�����ɗ����Ԃ��Č����ʂ�l����̂��R�c�ł��B
(1) ������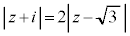 �����_z�S�̂��\���}�`�́A�_
�����_z�S�̂��\���}�`�́A�_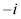 �Ɠ_
�Ɠ_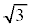 ���A2�F1�ɓ�������_
���A2�F1�ɓ�������_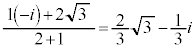 �ƁA2�F1�ɊO������_
�ƁA2�F1�ɊO������_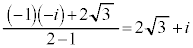 �a�̗��[�Ƃ���~�ɂȂ�܂�(�O�����Q��)�B
�a�̗��[�Ƃ���~�ɂȂ�܂�(�O�����Q��)�B 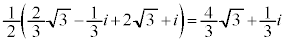 ......[�A]
......[�A]�~�̔��a�́A���a��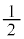 �ŁA
�ŁA 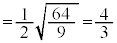 ......[�C]
......[�C]
(2) 1����30�܂ł̎��R���̒���6�܂���8�܂���9�Ŋ�������̂̌�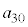 �́A6�C8�C9�C12�C16�C18�C24�C27�C30��9�ł��B
�́A6�C8�C9�C12�C16�C18�C24�C27�C30��9�ł��B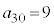 ......[�E]
......[�E] 6��8��9�̍ŏ����{����72�ł�(�������Q��)�B1����72�܂ł̎��R���̒��ŁA6�Ŋ�������̂́A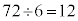 ����܂��B8�Ŋ�������̂�
����܂��B8�Ŋ�������̂�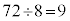 ����܂��B9�Ŋ�������̂�
����܂��B9�Ŋ�������̂�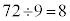 ����܂��B6��8�Ŋ�������̑���24�Ŋ�������̂�
����܂��B6��8�Ŋ�������̑���24�Ŋ�������̂�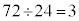 ����܂��B8��9�Ŋ�������̑���72�Ŋ�������̂�72������1�ł��B6��9�Ŋ�������̑���18�Ŋ�������̂�
����܂��B8��9�Ŋ�������̑���72�Ŋ�������̂�72������1�ł��B6��9�Ŋ�������̑���18�Ŋ�������̂�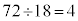 ����܂��B6��8��9�̂�����ł���������̂�72������1�ł��B1����72�܂ł̎��R���̒���6�܂���8�܂���9�Ŋ�������̂́A
����܂��B6��8��9�̂�����ł���������̂�72������1�ł��B1����72�܂ł̎��R���̒���6�܂���8�܂���9�Ŋ�������̂́A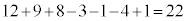 ����܂�(�W���̗v�f�̐����Q��)�B73����144�܂ł̎��R���̒���6�܂���8�܂���9�Ŋ�������̂�22����܂��Bm��0�ȏ�̐����Ƃ��āA
����܂�(�W���̗v�f�̐����Q��)�B73����144�܂ł̎��R���̒���6�܂���8�܂���9�Ŋ�������̂�22����܂��Bm��0�ȏ�̐����Ƃ��āA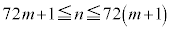 �ƂȂ鎩�R��n�̒���6�܂���8�܂���9�Ŋ�������̂�22����܂��B
�ƂȂ鎩�R��n�̒���6�܂���8�܂���9�Ŋ�������̂�22����܂��B
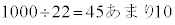 �Ȃ̂ŁA1����
�Ȃ̂ŁA1����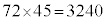 �܂ł̎��R���̒���6�܂���8�܂���9�Ŋ�������̂�
�܂ł̎��R���̒���6�܂���8�܂���9�Ŋ�������̂�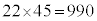 ����܂��B[�E]���A3241����3270�܂ł̎��R���̒���6�܂���8�܂���9�Ŋ�������̂�9����A1����3270�܂ł̎��R���̒���6�܂���8�܂���9�Ŋ�������̂�
����܂��B[�E]���A3241����3270�܂ł̎��R���̒���6�܂���8�܂���9�Ŋ�������̂�9����A1����3270�܂ł̎��R���̒���6�܂���8�܂���9�Ŋ�������̂�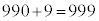 ����܂��B3271(72�Ŋ����31�]��)��6�ł�8�ł�9�ł������܂��A3272(72�Ŋ����32�]��)��8�Ŋ����܂��B32��8�Ŋ����܂����A33�C34�C35��6�ł�8�ł�9�ł�����ꂸ36��6��9�Ŋ����A72�Ŋ����33�]��3273�C72�Ŋ����34�]��3274�C72�Ŋ����35�]��3275�́A6�ł�8�ł�9�ł�����ꂸ�A72�Ŋ����36�]��3276��6��9�Ŋ�����̂ŁA
����܂��B3271(72�Ŋ����31�]��)��6�ł�8�ł�9�ł������܂��A3272(72�Ŋ����32�]��)��8�Ŋ����܂��B32��8�Ŋ����܂����A33�C34�C35��6�ł�8�ł�9�ł�����ꂸ36��6��9�Ŋ����A72�Ŋ����33�]��3273�C72�Ŋ����34�]��3274�C72�Ŋ����35�]��3275�́A6�ł�8�ł�9�ł�����ꂸ�A72�Ŋ����36�]��3276��6��9�Ŋ�����̂ŁA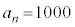 �����ő��n��
�����ő��n��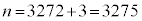 ......[�G]
......[�G]
(3) 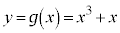 �ɂ����āAx��y�����ւ��A
�ɂ����āAx��y�����ւ��A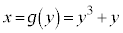 �C�����y�ɂ��ĉ���(�t�����Q��)�A
�C�����y�ɂ��ĉ���(�t�����Q��)�A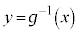 ��
�� 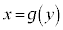 �@����@
�@����@ �ɒ��ӂ��܂��B�@�̂Ƃ��A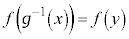 �ł��B
�ł��B 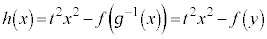 �@(
�@(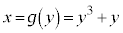 )�@����A
)�@����A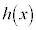 ��
��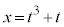 �ɂ����ċɒl���Ƃ�(���̑������Q��)�̂ŁA
�ɂ����ċɒl���Ƃ�(���̑������Q��)�̂ŁA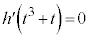 ���A
���A����āA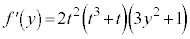 �@����B
�@����B
�Ƃ���ŁA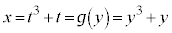 �̂Ƃ��A�܂�A
�̂Ƃ��A�܂�A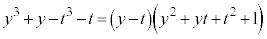 �̂Ƃ��A
�̂Ƃ��A ���J�b�R���͐��Ȃ̂ŁA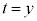
�B��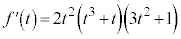 �Ƃ��āA
�Ƃ��āA 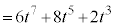
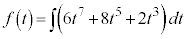 ......[��]
......[��]������t ��C�ӂ̎����Ƃ���t ���ϕ������ƁA 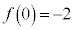 (C�F�ϕ��萔)
(C�F�ϕ��萔)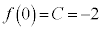 ���A
���A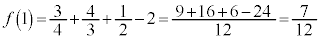
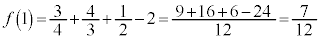 ......[��]
......[��]
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@�c�嗝�H���wTOP�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B�Ȃ��A�́A
��w�y�w�m����ł��B©2005-2025(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B