�c�嗝�H���w'25�N[4]
�ȉ��̐ݖ�ł́A���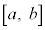 �ŘA���Ȋ�
�ŘA���Ȋ�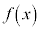 �C
�C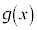 �C
�C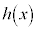 �ɑ��āA���
�ɑ��āA���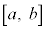 ��
��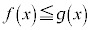 �Ȃ��
�Ȃ��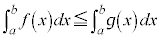 �ł��邱�ƁA�����
�ł��邱�ƁA�����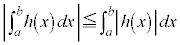 �ł��邱�Ƃ����Ƃ��Ȃ��ɗp���Ă悢�B
�ł��邱�Ƃ����Ƃ��Ȃ��ɗp���Ă悢�B
(1) ���R��n�ɑ���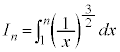 �Ƃ���B���̂Ƃ��A
�Ƃ���B���̂Ƃ��A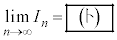 �ł���B
�ł���B (2) ���R��n�ɑ���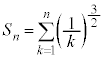 �Ƃ���B���ׂĂ�n�ɑ��ĕs����
�Ƃ���B���ׂĂ�n�ɑ��ĕs���� ���ؖ����Ȃ����B
(3) 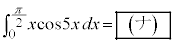 �ł���B
�ł���B (4) k�����R���Ƃ���Ƃ��A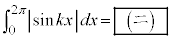 �ł���B
�ł���B (5) 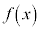 ������\�Ȋ��Ƃ��AM�𐳂̒萔�Ƃ���B���
������\�Ȋ��Ƃ��AM�𐳂̒萔�Ƃ���B���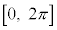 �ŁA
�ŁA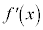 �͘A������
�͘A������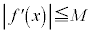 �Ɖ��肷��B���R��k�Cn�ɑ��āA
�Ɖ��肷��B���R��k�Cn�ɑ��āA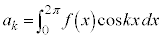 �Ƃ��A
�Ƃ��A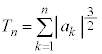 �Ƃ���B���̂Ƃ��A���ׂĂ�n�ɑ��ĕs����
�Ƃ���B���̂Ƃ��A���ׂĂ�n�ɑ��ĕs���� ���ؖ����Ȃ����B�������A�K�v�ł����(2)�̕s������(4)�̓������ؖ��Ȃ��ɗp���Ă悢�B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@�S�^�S�^���Ă���悤�Ɍ����܂����A�U���ʂ�i�߂čs���S�[���ɂ��ǂ���܂��B
(1) 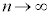 �̂Ƃ��A
�̂Ƃ��A �� 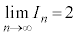 ......[�g]
......[�g] (2) 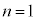 �̂Ƃ��A
�̂Ƃ��A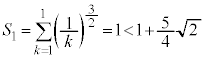 ��萬�����܂��B
��萬�����܂��B 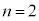 �̂Ƃ��A
�̂Ƃ��A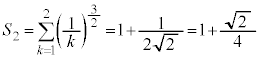 �@����@
�@����@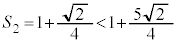 ��萬�����܂��B
��萬�����܂��B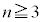 �̂Ƃ��A
�̂Ƃ��A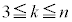 ��������k�ɑ��A
��������k�ɑ��A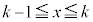 �ɂ�����
�ɂ�����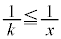 ���
���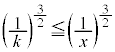
��蕶�ɏ�����Ă���s������p���āA
����āA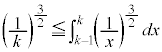
������A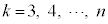 �ɂ��ĉ������킹��ƁA
�ɂ��ĉ������킹��ƁA ����āA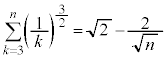 �@����A
�@����A
�@�{�A���A ����ӂ͐������܂��B
�ȏ���A���ׂĂ̎��R��n�ɑ��āA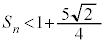 ���������܂��B(�ؖ��I)
���������܂��B(�ؖ��I) 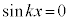 ����x�́Aj�𐮐��Ƃ��āA
����x�́Aj�𐮐��Ƃ��āA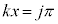 ���
���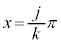 �ł����A�ϕ����
�ł����A�ϕ����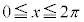 �ɂ����ẮA
�ɂ����ẮA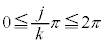 ���
���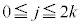 �ł��B�����ŁA�ϕ����
�ł��B�����ŁA�ϕ����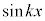 ��
��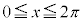 �̋��
�̋��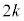 (
(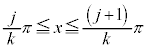 )�ɕ����čl���܂��B
)�ɕ����čl���܂��B
�O�p���͎������ł��B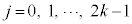 �ɂ����āA
�ɂ����āA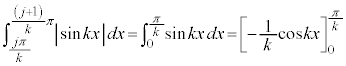 �Ƃ��āA
�Ƃ��āA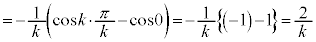 �ł����
�ł����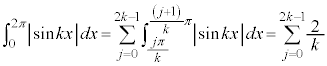 �C
�C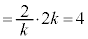 �ł����
�ł����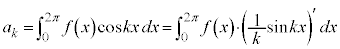 �Ȃ̂ŁA
�Ȃ̂ŁA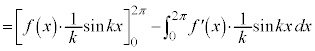 (
(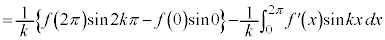 (
(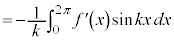 ))�ł��B
))�ł��B
����āA�Ȃ̂ŁA
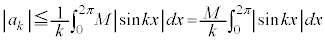 ......[�j]
......[�j](5) 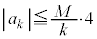
��蕶�̕s������p���āA
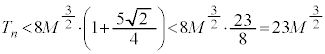 ���A
���A(4)�̌��ʂ�p���āA
(2)�̌��ʂ�p���āA
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@�c�嗝�H���wTOP�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B�Ȃ��A�́A
��w�y�w�m����ł��B©2005-2025(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B 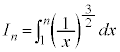 �Ƃ���B���̂Ƃ��A
�Ƃ���B���̂Ƃ��A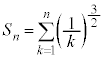 �Ƃ���B���ׂĂ�n�ɑ��ĕs����
�Ƃ���B���ׂĂ�n�ɑ��ĕs����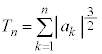 �Ƃ���B���̂Ƃ��A���ׂĂ�n�ɑ��ĕs����
�Ƃ���B���̂Ƃ��A���ׂĂ�n�ɑ��ĕs����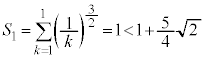 ��萬�����܂��B
��萬�����܂��B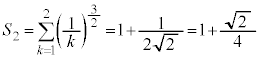 �@����@
�@����@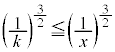
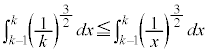
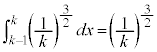
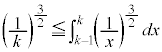
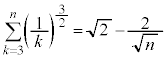 �@����A
�@����A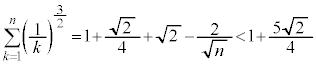
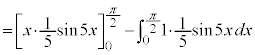
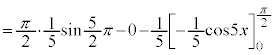
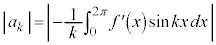
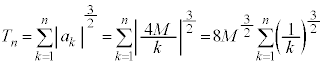
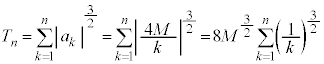
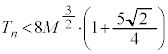
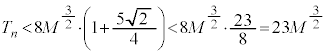 �@(�ؖ��I)
�@(�ؖ��I)