���嗝�n���w'02�N�O��[3]
 �͐������W���Ƃ���x��4�����Ƃ���B4��������
�͐������W���Ƃ���x��4�����Ƃ���B4�������� �̏d�������߂�4�̉��̂����A2�͐�����2�͋����ł���Ƃ����B���̂Ƃ�a�Cb�Cc�̒l�����߂�B
�̏d�������߂�4�̉��̂����A2�͐�����2�͋����ł���Ƃ����B���̂Ƃ�a�Cb�Cc�̒l�����߂�B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@4���������F �̐�������p�Cq�C������(�����W����4���������Ȃ̂ŁA�݂��ɋ����ɂȂ�)��
�̐�������p�Cq�C������(�����W����4���������Ȃ̂ŁA�݂��ɋ����ɂȂ�)��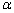 �C
�C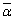 �Ƃ��܂�(�������������Q��)�B
�Ƃ��܂�(�������������Q��)�B
4���������̊e���̌W�����r���āA
�@���A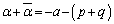 ����D
����D
�E�ӂ͐����Ȃ̂ŁA �������ł��B
�������ł��B
�A���A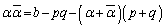
�E�ӂ͐����Ȃ̂ŁA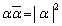 �������ł��B
�������ł��B
�C���A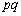 �C
�C ��1�̖ł����āA
��1�̖ł����āA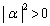 ���A
���A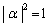 ����E �Ɍ����܂��B�]���āA
����E �Ɍ����܂��B�]���āA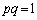 �ł��B����āA
�ł��B����āA
(i) 
(ii) 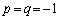
��2�̏ꍇ���l����悢���ƂɂȂ�܂��B
 �܂�
�܂�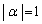 ���Aα�͒P�ʉ~��(���_�𒆐S�Ƃ��锼�a1�̉~)�̓_��\�����f���ł��B
���Aα�͒P�ʉ~��(���_�𒆐S�Ƃ��锼�a1�̉~)�̓_��\�����f���ł��B
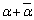 �́Aα�̎���
�́Aα�̎���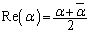 ��2�{�Ȃ̂ŁA
��2�{�Ȃ̂ŁA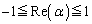 ���A
���A
�A���A �̂Ƃ��ɂ́A
�̂Ƃ��ɂ́A �Ɍ����Ă��܂��A���̂Ƃ��ɂ�
�Ɍ����Ă��܂��A���̂Ƃ��ɂ�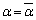 �͋����łȂ��Ȃ��Ă��܂��܂��B�]���āA
�͋����łȂ��Ȃ��Ă��܂��܂��B�]���āA ����F
����F
(i) 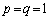 �̂Ƃ��A
�̂Ƃ��A �D���A
�A�C�E���A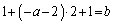
�� 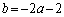 �B���A
�B���A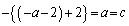
�F���A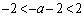
��  �]���Đ���a�́A
�]���Đ���a�́A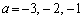
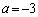 �̂Ƃ��A
�̂Ƃ��A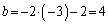 �C
�C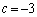
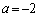 �̂Ƃ��A
�̂Ƃ��A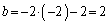 �C
�C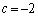
 �̂Ƃ��A
�̂Ƃ��A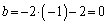 �C
�C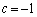
(ii) 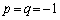 �̂Ƃ��A
�̂Ƃ��A �D���A
�A�C�E���A
�� 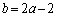 �B���A
�B���A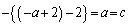
�F���A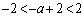
�� 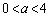 �]���Đ���a�́A
�]���Đ���a�́A
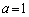 �̂Ƃ��A
�̂Ƃ��A �C
�C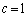
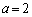 �̂Ƃ��A
�̂Ƃ��A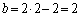 �C
�C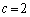
 �̂Ƃ��A
�̂Ƃ��A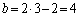 �C
�C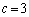
�ȏ���A
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���嗝�n���wTOP�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B