���嗝�n���w'06�N�O��[5]
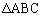 �ɑ��A��AB��ɓ_P���A��BC��ɓ_Q���A��CA��ɓ_R���A���_�Ƃ͈قȂ�悤�ɂƂ�B����3�_�����ꂼ��̕ӏ���Ƃ��A����3�_�_�Ƃ���O�p�`�̏d�S�͂ǂ̂悤�Ȕ͈͂����}������B
�ɑ��A��AB��ɓ_P���A��BC��ɓ_Q���A��CA��ɓ_R���A���_�Ƃ͈قȂ�悤�ɂƂ�B����3�_�����ꂼ��̕ӏ���Ƃ��A����3�_�_�Ƃ���O�p�`�̏d�S�͂ǂ̂悤�Ȕ͈͂����}������B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@���ʃx�N�g���̖��ł��B�x�N�g���̓����E�O���A���ʃx�N�g���̉��p���Q�Ƃ��Ă��������B�O�p�`�̏d�S��G�Ƃ��āA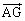 ��2�̃x�N�g��
��2�̃x�N�g��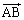 �C
�C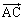 ���g���ĕ\�����Ƃɂ��d�S�̑��ݔ͈͂��l���܂��B
���g���ĕ\�����Ƃɂ��d�S�̑��ݔ͈͂��l���܂��B
���������߂邾���Ȃ�ȒP�ł����A������Ƙ_����̂͂Ȃ��Ȃ�������ł��B
P�͕�AB��̒��_�Ƃ͈قȂ�_������A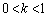 �Ƃ��āA
�Ƃ��āA
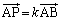 �@����@
�@����@
Q�͕�BC ��̒��_�Ƃ͈قȂ�_������A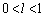 �Ƃ��āA
�Ƃ��āA
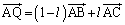 �@����A
�@����A
R�͕�CA��̒��_�Ƃ͈قȂ�_������A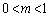 �Ƃ��āA
�Ƃ��āA
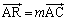 �@����B
�@����B
�O�p�`PQR�̏d�S��G�Ƃ��āA
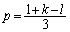 �C
�C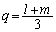 �@����C
�@����C
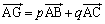 �@����D
�@����D
���āAk�Cl�Cm�ɂ��āA
�Ƃ�������������܂����A�C�̒��ɓo�ꂷ��A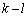 �C
�C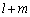 �ɂ��ẮA
�ɂ��ẮA
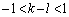 �C
�C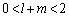 �@����F
�@����F
�������A�F�����悤��k�Cl�Cm���Ƃ��āA�Ⴆ�A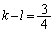 �C
�C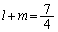 �Ƃ��Ă��F�͖�������܂����A
�Ƃ��Ă��F�͖�������܂����A
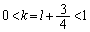 �C
�C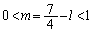
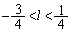 �C��҂��
�C��҂��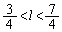 �ƂȂ��Ă��܂��āA�E�����悤��k�Cl�Cm���Ƃ邱�Ƃ��ł��܂���(��ӂ����O�p�`PQR����邱�Ƃ��ł��Ȃ�)�B
�ƂȂ��Ă��܂��āA�E�����悤��k�Cl�Cm���Ƃ邱�Ƃ��ł��܂���(��ӂ����O�p�`PQR����邱�Ƃ��ł��Ȃ�)�B
�܂�A�F�����ł́A�����s���Ȃ̂ł��B�����ŁA�F�ɏ����������āA���̏��������������A�E����k�Cl�Cm�̑g���K�����݂���悤�ɂ��܂��B
�C�ŁA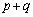 ���l�����l��������
���l�����l��������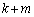 ���o�Ă���̂ŁA
���o�Ă���̂ŁA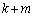 �̎�蓾��l���l���A�F�ɁA
�̎�蓾��l���l���A�F�ɁA
�Ƃ��������������A
�Ƃ��܂��B
�G����k�Cl�Cm���Ƃ�ƁA��2���ƁA��3������A
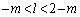 �C
�C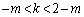
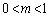 �����ǂ̂悤�Ȓl�ɂ��Ă��A�G�̑�1���ƇE�����ׂĖ������悤�ȁAk�Cl���Ƃ邱�Ƃ��ł��܂�(�G�̏�������k�Cl�Cm�̑g��1�g�ł����݂���Α�ӂ����O�p�`PQR����邱�Ƃ��ł��܂�)�B
�����ǂ̂悤�Ȓl�ɂ��Ă��A�G�̑�1���ƇE�����ׂĖ������悤�ȁAk�Cl���Ƃ邱�Ƃ��ł��܂�(�G�̏�������k�Cl�Cm�̑g��1�g�ł����݂���Α�ӂ����O�p�`PQR����邱�Ƃ��ł��܂�)�B
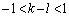 ���A
���A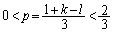
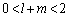 ���A
���A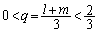
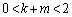 ���A
���A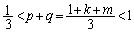
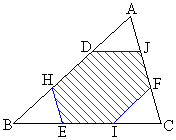
�E�}�ŁA��AB��3��������_��A������AD�CH�Ƃ��܂��B
��BC��3��������_��B������AE�CI�Ƃ��܂��B
��CA��3��������_��C������AF�CJ�Ƃ��܂��B
�D���Œ�߂�_G�ɂ��āA
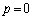 �����̂́A
�����̂́A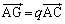 ���A����AC��̓_�B
���A����AC��̓_�B
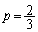 �����̂́A
�����̂́A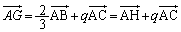 ���A����HE��̓_�B
���A����HE��̓_�B
 ����āA
����āA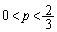 �����̂́A����AC�ƒ���HE�ɋ��܂ꂽ����(�������������)�B
�����̂́A����AC�ƒ���HE�ɋ��܂ꂽ����(�������������)�B
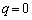 �����̂́A����AB��̓_�B
�����̂́A����AB��̓_�B
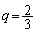 �����̂́A����FI��̓_�B
�����̂́A����FI��̓_�B
����āA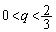 �����̂́A����AB�ƒ���FI�ɋ��܂ꂽ����(�������������)�B
�����̂́A����AB�ƒ���FI�ɋ��܂ꂽ����(�������������)�B
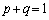 �����̂́A����BC��̓_�B
�����̂́A����BC��̓_�B
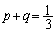 �����̂́A����DI��̓_�B
�����̂́A����DI��̓_�B
����āA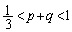 �����̂́A����BC�ƒ���DI�ɋ��܂ꂽ����(�������������)�B
�����̂́A����BC�ƒ���DI�ɋ��܂ꂽ����(�������������)�B
�ȏ���A���߂�͈͂́A�E�}�ΐ����̘Z�p�`DHEIFJ�̓���(���E���͊܂܂Ȃ�)�B ......[��]
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���嗝�n���wTOP�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B