���嗝�n���w'07�N�O����[5]
A��2���̐����s��Ƃ���B��x�N�g��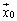 �ɑ��A��x�N�g��
�ɑ��A��x�N�g��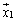 �C
�C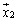 �C�����
�C�����
�@�@�@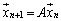 �@(
�@(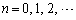 )
)
�ɂ���Ē�߂�B����[���x�N�g���ł͂Ȃ� �ɂ��āA3�ȏ�̎��R��m�ŏ��߂�
�ɂ��āA3�ȏ�̎��R��m�ŏ��߂�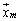 ��
��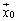 �ƈ�v����Ƃ��A�s��
�ƈ�v����Ƃ��A�s��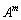 �͒P�ʍs��ł��邱�Ƃ������B
�͒P�ʍs��ł��邱�Ƃ������B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@�s�� ���o�Ă���̂ŁA�n�~���g���E�P�[���[�̒藝�Ŏ����������s�����A�ŗL�l�E�ŗL�x�N�g�����l���邩�ł��B�ŗL�l�ł́A
���o�Ă���̂ŁA�n�~���g���E�P�[���[�̒藝�Ŏ����������s�����A�ŗL�l�E�ŗL�x�N�g�����l���邩�ł��B�ŗL�l�ł́A �Ƃ��������������ɂ����̂ŁA�����������l���邱�Ƃɂ��܂��B
�Ƃ��������������ɂ����̂ŁA�����������l���邱�Ƃɂ��܂��B
�܂��A�s��A�ׂ̂��悪�A�s��A��1�����ŕ\���邱�ƁA�܂�Ak��2�ȏ�̐����Ƃ��āA ���A
���A
 �@(E��2���̒P�ʍs��A
�@(E��2���̒P�ʍs��A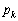 �C
�C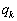 �͎���)
�͎���)
�Ƃ����`�ɕ\�킹��@���(��)�@���Ƃ��A���w�I�A�[�@�Ŏ����܂��B
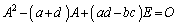 �@(O��2���̗�s��)����āA
�@(O��2���̗�s��)����āA
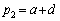 �C
�C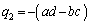 �Ƃ��āA
�Ƃ��āA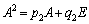 �@(
�@( �C
�C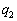 �͎����A���Z�͈̔͂ł͍s��̐����͎����ł�)�ƕ\���܂��B
�͎����A���Z�͈̔͂ł͍s��̐����͎����ł�)�ƕ\���܂��B(�U) 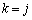 �̂Ƃ��A
�̂Ƃ��A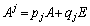 (
(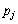 �C
�C �͎���)�ƕ\����Ƃ��āA
�͎���)�ƕ\����Ƃ��āA 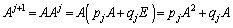 (�T)���A
(�T)���A
����āA �C
�C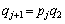 �Ƃ���A
�Ƃ���A �C
�C �͎����ŁA������A
�͎����ŁA������A

�ƕ\���܂��B �ƕ\���܂��B
�ƕ\���܂��B
(��)���A �@����@�@�ƕ\���܂��B
�@����@�@�ƕ\���܂��B
 ����A
����A
 �@����A
�@����A
(i)  �̂Ƃ��A
�̂Ƃ��A
���ӂ�A�������āA
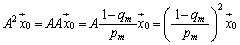 �@����B
�@����B
�Ȍ�A����Ԃ�A�������邱�Ƃɂ��A
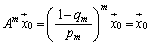
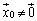 �ł���A
�ł���A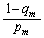 �͎����Ȃ̂ŁA
�͎����Ȃ̂ŁA
���̂Ƃ��B���A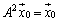 �ƂȂ�A
�ƂȂ�A �Ƃ��������ɖ������܂��B����āA���̏ꍇ�͕s�K�ł��B
�Ƃ��������ɖ������܂��B����āA���̏ꍇ�͕s�K�ł��B (ii) 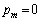 �̂Ƃ��A�A���A
�̂Ƃ��A�A���A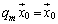
�ȏ���A�s�� �͒P�ʍs��ł��B
�͒P�ʍs��ł��B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���嗝�n���wTOP�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B