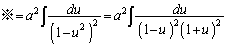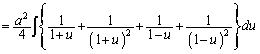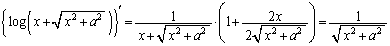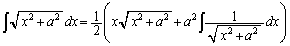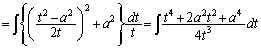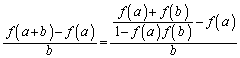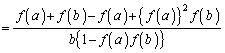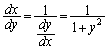���s��w���n2007�N���w�������
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�b[1]�@���̊e��ɂ��ꂼ�ꓚ����B
��1�D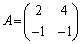 �C
�C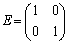 �Ƃ���Ƃ��A
�Ƃ���Ƃ��A 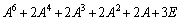 �����߂�B
�����߂�B
��2�D���_1�C2�C����Cn���������m���œ�����Q�[����Ɨ���3��J��Ԃ��B���̂Ƃ��A2��ڂ̓��_��1��ڂ̓��_�ȏ�ł���A�����3��ڂ̓��_��2��ڂ̓��_�ȏ�ƂȂ�m�������߂�B
[��]
�b[2]�@x�Cy�𑊈قȂ鐳�̎����Ƃ���B����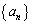 ��
��
�@�@�@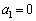 �C
�C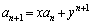 (
(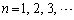 )
)
�ɂ���Ē�߂�Ƃ��A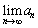 ���L���̒l�Ɏ�������悤�ȍ��W���ʏ�̓_
���L���̒l�Ɏ�������悤�ȍ��W���ʏ�̓_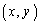 �͈̔͂�}������B
�͈̔͂�}������B
[��]
�b[3]�@p��3�ȏ�̑f���Ƃ���B4�̐���a�Cb�Cc�Cd������3����
�@�@�@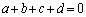 �C
�C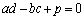 �C
�C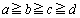
�����Ƃ��Aa�Cb�Cc�Cd��p��p���ĕ\���B
[��]
�b[4]�@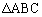 �ɂ����āA
�ɂ����āA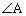 �̓����Ƃ��̎O�p�`�̊O�ډ~�Ƃ̌�_��A�ƈقȂ�_��
�̓����Ƃ��̎O�p�`�̊O�ډ~�Ƃ̌�_��A�ƈقȂ�_��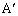 �Ƃ���B���l��
�Ƃ���B���l��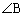 �C
�C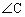 �̓����Ƃ��̊O�ډ~�Ƃ̌�_�����ꂼ��
�̓����Ƃ��̊O�ډ~�Ƃ̌�_�����ꂼ��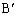 �C
�C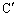 �Ƃ���B���̂Ƃ�3����
�Ƃ���B���̂Ƃ�3����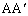 �C
�C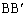 �C
�C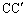 ��1�_H�Ō����A���̓_H�͎O�p�`
��1�_H�Ō����A���̓_H�͎O�p�`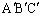 �̐��S�ƈ�v���邱�Ƃ��ؖ�����B
�̐��S�ƈ�v���邱�Ƃ��ؖ�����B
[��]
�b[5]�@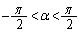 �Ƃ���B���W���ʏ�Ō��_�̎����
�Ƃ���B���W���ʏ�Ō��_�̎����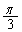 ��]����1���ϊ���f�Ƃ��A����
��]����1���ϊ���f�Ƃ��A���� �ɂ��đΏ̈ړ�����1���ϊ���g�Ƃ���B�����ϊ�
�ɂ��đΏ̈ړ�����1���ϊ���g�Ƃ���B�����ϊ�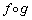 ��x���ɂ��đΏ̈ړ�����1���ϊ��ƈ�v����Ƃ��Aα�̒l�����߂�B
��x���ɂ��đΏ̈ړ�����1���ϊ��ƈ�v����Ƃ��Aα�̒l�����߂�B
[��]
�b[6]�@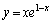 ��
��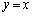 �̃O���t�ň͂܂ꂽ������x���̉��ɉ�]���Ăł��闧�̂̑̐ς����߂�B
�̃O���t�ň͂܂ꂽ������x���̉��ɉ�]���Ăł��闧�̂̑̐ς����߂�B
[��]
��[1]�@�ȉ��̊e��ɂ��ꂼ�ꓚ����B
��1�D��ϕ�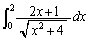 �����߂�B
�����߂�B ��2�D1����1�i�܂���2�i�̂����ꂩ�ŊK�i������Ƃ��A1����2�i���邱�Ƃ͘A�����Ȃ����̂Ƃ���B15�i�̊K�i�����鏸����͉��ʂ肠�邩�B
[��]
��[2]�@�b[2]�Ɠ���
��[3]�@�b[3]�Ɠ���
��[4]�@�_O�𒆐S�Ƃ���~�ɓ��ڂ���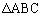 ��3��AB�CBC�CCA�����ꂼ��2�F3�ɓ�������_��P�CQ�CR�Ƃ���B
��3��AB�CBC�CCA�����ꂼ��2�F3�ɓ�������_��P�CQ�CR�Ƃ���B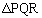 �̊O�S��O�ƈ�v����Ƃ��A
�̊O�S��O�ƈ�v����Ƃ��A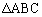 �͂ǂ̂悤�ȎO�p�`���B
�͂ǂ̂悤�ȎO�p�`���B
[��]
��[5]�@A��2���̐����s��Ƃ���B��x�N�g��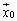 �ɑ��A��x�N�g��
�ɑ��A��x�N�g��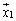 �C
�C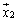 �C�����
�C�����
�@�@�@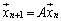 �@(
�@(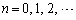 )
)
�ɂ���Ē�߂�B����[���x�N�g���ł͂Ȃ�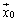 �ɂ��āA3�ȏ�̎��R��m�ŏ��߂�
�ɂ��āA3�ȏ�̎��R��m�ŏ��߂�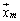 ��
��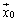 �ƈ�v����Ƃ��A�s��
�ƈ�v����Ƃ��A�s��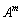 �͒P�ʍs��ł��邱�Ƃ������B
�͒P�ʍs��ł��邱�Ƃ������B
[��]
��[6]�@���ׂĂ̎����Œ�`���ꉽ��ł������ł����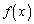 ��
��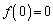 �C
�C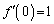 �����A����ɔC�ӂ̎���a�Cb�ɑ���
�����A����ɔC�ӂ̎���a�Cb�ɑ���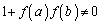 �ł����āA
�ł����āA
�@�@�@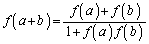
��������B
(1) �C�ӂ̎���a�ɑ��āA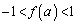 �ł��邱�Ƃ��ؖ�����B
�ł��邱�Ƃ��ؖ�����B (2) 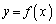 �̃O���t��
�̃O���t��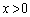 �ŏ�ɓʂł��邱�Ƃ��ؖ�����B
�ŏ�ɓʂł��邱�Ƃ��ؖ�����B [��]
�e�⌟��
�b[1](��������)�@��1�́A�n�~���g���E�P�[���[�̒藝��p���āA�s��̑������̎�����������Ƃ����T�^���ł��B�s��ɂ͏��Z���Ȃ��̂ŁA���^��(x�Ɋւ���)�������ŏ��Z���s�����ƂɂȂ�܂��B�����A�s��A�̑�����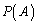 ������Ƃ��Ax�̑�����
������Ƃ��Ax�̑�����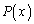 �𑽍���
�𑽍���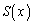 �Ŋ������Ƃ��ɏ���
�Ŋ������Ƃ��ɏ���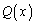 �C�]�肪
�C�]�肪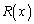 ���Ƃ��āA
���Ƃ��āA
���̂Ƃ��Ax���s��A�ɑウ�Ăł��铙��
�����藧���܂��B�����ŁA�n�~���g���E�P�[���[�̒藝�ɂ���āA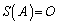 (��s��)�ƂȂ�̂ł���A
(��s��)�ƂȂ�̂ł���A
�ł��B
��2�́A1����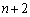 �̈قȂ�
�̈قȂ�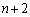 �ʂ�̐��̒�����3�̐���I���(
�ʂ�̐��̒�����3�̐���I���(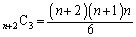 �ʂ�)�A����������x�Cy�Cz�Ƃ���(
�ʂ�)�A����������x�Cy�Cz�Ƃ���(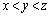 )�Ƃ��Ay����1�������āAz����2�������A
)�Ƃ��Ay����1�������āAz����2�������A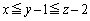 �ƂȂ�A���̖���3��̓��_�̏��������܂��B���̍l�������A�����Ƃ��ȒP�����m��܂���B
�ƂȂ�A���̖���3��̓��_�̏��������܂��B���̍l�������A�����Ƃ��ȒP�����m��܂���B
�b[2](��������)�@2���ԑQ�����̉�@�Ɠ��䐔��̋Ɍ���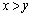 �C
�C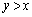 �ɏꍇ�������čl���邾���̖��ł��B
�ɏꍇ�������čl���邾���̖��ł��B
�ƕό`���āA���̌`�ɂ��Ă��܂��ƁA���ɂ����Ȃ�̂ŁA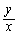 �C
�C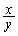 ���c���`�ōl����̂��R�c�ł��B
���c���`�ōl����̂��R�c�ł��B
�b[3](��������)�@�������ŕ����������̂ŁA��u�r�r��܂����A2�̓�������1�����������Ă��܂��ƁA�������Ƃ��ēT�^�I�Ȍ`�A
����A�~����B������C (����A�Ɛ���B�͐���C�̖�)
���o�Ă��܂��B
��蕶�������ƌ��߂��܂܍d�����Ă��܂��Ɛ�ɂ͐i�߂܂���B�����������ł́A�Ƃɂ���������āA�B��Ă�������������o�����Ƃ���ł��B
�܂��A�̓r���ŁA
�Ƃ����s�������o�Ă��܂��B�������ł́A�����������C�Ȃ��s�����ɂ��������B��Ă��܂��B�����2������̂ŁAp�͋���������A�Ƃ����ɍl����悤�ɂ��������̂ł��B�����ł́Ap��3�ȏ�̑f���Ȃ̂Ŋ�A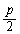 ��
��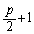 �������ł͂Ȃ��A�Ƃ������ƂɂȂ�A����ŁA����a���m�肵�Ă��܂��̂ł��B���C�Ȃ��ޏ�(�ގ�)�̎d���̂�����������ȐS�̈��ɋC�Â��������̂ł��B
�������ł͂Ȃ��A�Ƃ������ƂɂȂ�A����ŁA����a���m�肵�Ă��܂��̂ł��B���C�Ȃ��ޏ�(�ގ�)�̎d���̂�����������ȐS�̈��ɋC�Â��������̂ł��B
�b[4](��������)�@��Ƃ苳�猩�����ɔ����āA���ʊ̏ؖ��͒��w�Z�ɖ߂��čs���Ǝv����̂ŁA�����������͑�w��������͏����Ă䂭�^���ɂ��邩���m��܂���B�ł����A���̏��͍̂���̑�w�����ɂ������p�������̂Ȃ̂ŁA�~����ɓ_������Ƃ��Ċp���l������ł́A�~���p�⒆�S�p���l����A�Ƃ������Ƃ��L�[���[�h�ł��邱�Ƃɂ͕ς��Ȃ����낤�Ǝv���܂��B
�{�����܂��A�~���p���l���邱�Ƃɂ��e�Ղɉ����ł��܂��B3����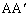 �C
�C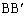 �C
�C ��1�_H�Ō���邱�Ƃɂ��ẮAH���O�p�`ABC�̓��S�ł��邱�Ƃ������Ώ\���ł��傤�B������Ŏ��Ԃ��]���ăq�}�ł���A�O�p�`�̊e���p��2��������1�_�Ō���邱�Ƃ̏ؖ������Ă����Ηǂ��Ǝv���܂��B
��1�_H�Ō���邱�Ƃɂ��ẮAH���O�p�`ABC�̓��S�ł��邱�Ƃ������Ώ\���ł��傤�B������Ŏ��Ԃ��]���ăq�}�ł���A�O�p�`�̊e���p��2��������1�_�Ō���邱�Ƃ̏ؖ������Ă����Ηǂ��Ǝv���܂��B
�b[5](��������)�@���N�������߂Ă���ƁA�߂܂��邵�����Z�ے��̓��e��Z���^�[�����͈̔͂��R���R���ς��̂ŁA1���ϊ��͍��Z�͈̔͂Ȃ̂��A2���ԑQ�����̓Z���^�[�����ŏo��̂��A����Y�܂��Ă��܂��܂��B���ȏȂ̂���l����̋C�܂���ɐU���A1�N����2�N���ƂňႤ�J���L�������ɂȂ����肷�鍂�Z�̐搶��������ς��낤�Ǝv���܂��B���s��w�ł́A�����̏o��͈͂��w�K�w���v�̂ɒǐ�������̂���߂Ă��܂��܂����B�l�I�ɂ́A�J���L���������e�́A��Ƃ苳��ł��낤�ƂȂ��낤�ƕς���ׂ��ł͂Ȃ��A�e���ڂ̐[��������Ηǂ��Ǝv���܂����A���ȏȂ̂���l����ɂ͑Ώ̕ϊ��Ɖ�]�ϊ��̈Ⴂ���킩���Ă��炦�Ȃ��̂����m��܂���B
�Ώ̈ړ��̍s��Ɖ�]�ړ��̍s������킹�Ē����s��Ƃ����A�x�N�g���ɂ������Ƃ��ɁA�x�N�g���̑傫����ς��Ȃ��A�Ƃ�������������܂��B2���̍s��ł́A�����s��́A
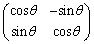 �C
�C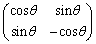
��2�ʂ�Ɍ����܂��B�O�҂��pθ �̉�]�ړ���\���A��҂�����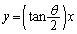 �Ɋւ���Ώ̈ړ���\���܂��B
�Ɋւ���Ώ̈ړ���\���܂��B
���̖��́A�����m���Ƃ��Ă����Ă��āA�s��̐ς̌v�Z���s���A�O�p���̉��@�藝���g���A�e�Ղɉɂ��ǂ���܂��B
�b[6](��������)�@��{�I�ȉ�]�̂̋��ϖ��ł��B�Ȑ�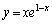 ����]���Ăł����]�̂̓������~����ɂ���ʂ���̂ŁA�Ȑ�����]���Ăł����]�̂̑̐ς���~���̑̐ς������Γ������o�܂��B
����]���Ăł����]�̂̓������~����ɂ���ʂ���̂ŁA�Ȑ�����]���Ăł����]�̂̑̐ς���~���̑̐ς������Γ������o�܂��B
�ł́A�����v�Z���債�����Ƃ͂Ȃ��̂ŁA�������đ����ׂĂ��܂����A�킩��₷�����邽�߂ł��B��]�̂̌`�����߂�悢�̂ŁA�ϕ��͈́A�����O�ɗ��ē��ɗ��邩�A�Ƃ����������悢�̂ł��B���ɂ���ẮA�����v�Z����ςȂ��̂�����̂ŁA���_�Ȏ��Ԃ��g��Ȃ��悤�ɒ��ӂ��Ă��������B
�����������ł́A�v�Z�~�X�������ɂȂ�܂��B�����̍̓_�ł��A���s��w�̑��Z�Ȑ搶���A�����ϕ��̓r���̌v�Z�ߒ��܂Œǂ��Ă����Ƃ͂ƂĂ��v���܂���B
�Ƃ�����ϕ����o�Ă��܂����A�����ϕ���2��s���ƁA�}�C�i�X�̌������Ⴂ������A2�Ŋ���̂�Y�ꂽ�肵�āA�v�Z�~�X��U�����₷���̂ŁA
�𗘗p���āA�ȉ��̂悤�Ȍv�Z����������v�Z�~�X��Ƃ��Ă͗ǂ������m��܂���B
�Ƃ���ƁA
�� 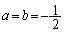 �C
�C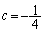
������A
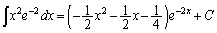 �@(C�F�ϕ��萔)
�@(C�F�ϕ��萔)
�J�͂͑債�ĕς��܂��A�v�Z�~�X�̃��X�N�͌���Ǝv���܂��B
��[1](��������)�@��1��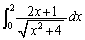 �Ƃ����ϕ��́A�܂��́A����
�Ƃ����ϕ��́A�܂��́A����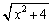 ��t�Ƃ����܂��B�ł����A
��t�Ƃ����܂��B�ł����A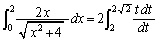 �ƂȂ��Ă��܂��̂ŁA
�ƂȂ��Ă��܂��̂ŁA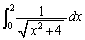 ���c���Ă��܂��܂��B
���c���Ă��܂��܂��B
�����́A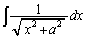 �Ƃ����`�ł����A
�Ƃ����`�ł����A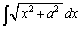 �Ƃ����`�̐ϕ������X�������܂�(
�Ƃ����`�̐ϕ������X�������܂�(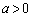 �Ƃ��܂�)�B�ǂ������Ԃ͂�����܂����A
�Ƃ��܂�)�B�ǂ������Ԃ͂�����܂����A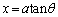 �Ƌ��ȏ����ɒu���Đϕ����s���܂��B
�Ƌ��ȏ����ɒu���Đϕ����s���܂��B
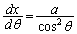 ���A
���A
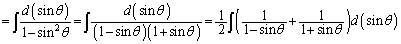
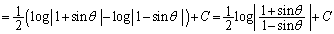 �@(C�F�ϕ��萔)
�@(C�F�ϕ��萔)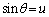 �Ƃ����ƁA
�Ƃ����ƁA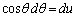
���̖��ł̓m�[�E�q���g�Ȃ̂ł����A�ʏ�́A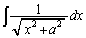 �́A
�́A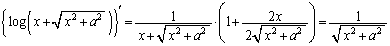
���Q�l�ɂ���A�Ƃ����q���g�����̂ŁA�q���g�ɏ]���āA
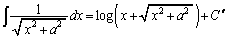 �@(
�@(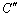 �F�ϕ��萔)�@����@
�F�ϕ��萔)�@����@
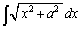 �ɂ��ẮA�����ϕ����s���āA
�ɂ��ẮA�����ϕ����s���āA
���A�E�ӂɏo�Ă���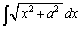 �����ӂɈڍ����āA
�����ӂɈڍ����āA
�����ŁA�@���g���āA
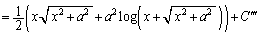 �@(
�@(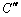 �F�ϕ��萔)
�F�ϕ��萔)
�ɏ������悤�ɁA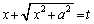 �ƒu���A
�ƒu���A
���A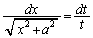
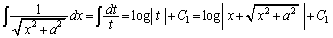 �@(
�@(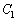 �F�ϕ��萔)
�F�ϕ��萔)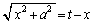 ��2�悵�āA
��2�悵�āA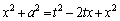
�� 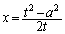
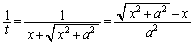 ���A
���A
�� 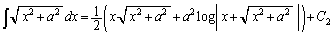
��2�́A�d���g�ݍ��킹���o�Ă��Ȃ��������A�ʉ��̕����ȒP�ɍς݂܂��B1����2�i����5��ȉ��Ƃ������Ƃ�����A�����ʒu��1��������Ȃ������ォ�����Ă��������ǂ��Ƃ������Ƃł��B
��[4](��������)�@�b[4]�͕��ʊʼn��܂������A���̖��́A�u�O�S�v�������̂ɁA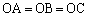 �C
�C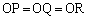 ���l����̂ł���A�}�`�Œ�������ɂ���̂ŁA�x�N�g�����ǂ��A�Ƃ������ƂɂȂ�܂��B
���l����̂ł���A�}�`�Œ�������ɂ���̂ŁA�x�N�g�����ǂ��A�Ƃ������ƂɂȂ�܂��B
�f���Ƀx�N�g���̑傫�����l���A���ς̊W�F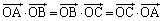 �������Ă��܂��A�ǂ̂悤�ɂ������ł��܂��B
�������Ă��܂��A�ǂ̂悤�ɂ������ł��܂��B
��[5](��������)�@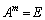 �Ȃ�A
�Ȃ�A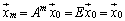 ������
������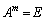 �ł���A�Ƃ����悤�ȉł́A�������A�_���͂��炦�܂���B�u3�ȏ�̎��R��m�ŏ��߂āv�Ƃ��������������Ƃ���Ă��܂��܂��B
�ł���A�Ƃ����悤�ȉł́A�������A�_���͂��炦�܂���B�u3�ȏ�̎��R��m�ŏ��߂āv�Ƃ��������������Ƃ���Ă��܂��܂��B
�s��ׂ̂���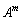 ���o�ꂷ��̂ł����A�s��A�̋�̓I�Ȍ`���^�����Ă���킯�ł͂Ȃ��A�s��ׂ̂�������߂�킯�ł��Ȃ������ł��B
���o�ꂷ��̂ł����A�s��A�̋�̓I�Ȍ`���^�����Ă���킯�ł͂Ȃ��A�s��ׂ̂�������߂�킯�ł��Ȃ������ł��B
�ł���A�n�~���g���E�P�[���[�Ŏ�����������̂��낤�A�Ƃ������ƂɂȂ�܂��B
A��2���̐����s��ł���A�n�~���g���E�P�[���[���g���ƁAA�ׂ̂���́AA��1�����ŕ\���܂��B����ŁA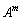 ��A��1�����ŕ\���Ă����A
��A��1�����ŕ\���Ă����A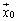 �ɂ����āA
�ɂ����āA
�Ƃ��̂��낤�A�Ƃ����A�E�g���C���������Ă��܂��B
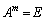 �Ƃ������Ƃ����������̂ŁA
�Ƃ������Ƃ����������̂ŁA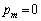 �C
�C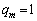 �����������킯�ł����A
�����������킯�ł����A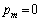 �ɂ��ẮA
�ɂ��ẮA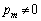 ���Ƃ��ĕςȂ��Ƃ��N���Ȃ����A�ƁA���҂���A�u3�ȏ�̎��R��m�ŏ��߂āv�Ƃ��������Ɋ���̏ꂪ�o�Ă���킯�ł��B
���Ƃ��ĕςȂ��Ƃ��N���Ȃ����A�ƁA���҂���A�u3�ȏ�̎��R��m�ŏ��߂āv�Ƃ��������Ɋ���̏ꂪ�o�Ă���킯�ł��B
�������ł́A�Ȃ��Ȃ������͂��܂����z�ł��Ȃ������m��܂���B���ɂ���ẮA���������@��Ԃ��āA�S���Ⴄ�p�x���璭�߂�Ɣ��z�ł���A�Ƃ�����������܂����A����ɔ�ׂ�A���̖��͎��R�Ȕ��z�ʼn�������ł��B
��[6](��������)�@��蕶���ɓo�ꂷ��W�������������ƌ����܂��B�ŋ߂̎��ɂ͕������������m��܂��A�ȑO�͓������Ƃ��Ă��悭���グ���Ă����e�[�}�ł��B�u�C�ӂ̎���a�Cb�v�ɑ��Đ������Ă���A�ƁA������Ă���̂ŁAa�Cb�ɓK���ɐ��l������Ă����ƁA���̐�����������邾���łȂ��A�̒NjL�ɏ������悤�ɁA���̌`�����߂Ă��܂����Ƃ��ł��܂��B
���̖��̊W���Ɨގ��̊W���F
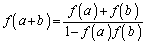 �@����@
�@����@
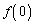 �����݂���Ƃ��āA
�����݂���Ƃ��āA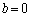 �Ƃ��Ă݂�ƁA
�Ƃ��Ă݂�ƁA
������āA
�� 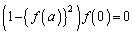
����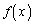 ���P���I��1�ł���Ƃ���ƁA�@�̕��ꂪ0�ƂȂ��āA
���P���I��1�ł���Ƃ���ƁA�@�̕��ꂪ0�ƂȂ��āA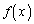 ����`�ł��Ȃ��Ȃ�̂ŁA
����`�ł��Ȃ��Ȃ�̂ŁA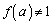 �ƂȂ�a���Ƃ�A
�ƂȂ�a���Ƃ�A
�ƂȂ�܂��B
x��0�ɋ߂��l�̂Ƃ��ɂ�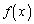 ����`�ł��āA���A�����\��
����`�ł��āA���A�����\��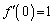 ���Ƃ��܂��Ba�Cb�C
���Ƃ��܂��Ba�Cb�C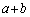 ��
��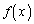 �̒�`����̎������Ƃ��āA
�̒�`����̎������Ƃ��āA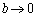 �Ƃ���ƁA
�Ƃ���ƁA
�]���āAx��0�ɋ߂��l�̂Ƃ��ɂ́A
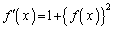 �@����A
�@����A
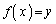 �C
�C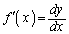 �Ə����āA
�Ə����āA
�t���̔����@�̌������A
����āA
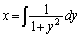 �@(�e00�N���嗝�n���[6]�Ŏ��グ���Ă��܂�)
�@(�e00�N���嗝�n���[6]�Ŏ��グ���Ă��܂�)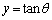 (
(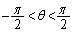 )�Ƃ����ƁA
)�Ƃ����ƁA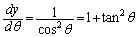
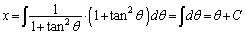 �@(C�F�ϕ��萔)
�@(C�F�ϕ��萔)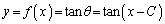
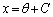 ��0�ɋ߂��l�Ȃ̂ŁA
��0�ɋ߂��l�Ȃ̂ŁA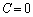 �Ƃ��܂��B
�Ƃ��܂��B
�� 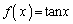
�W���@�́A���ڂ̉��@�藝�F
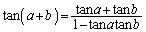 �@����B
�@����B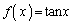 ���Ƃ������Ƃł��B
���Ƃ������Ƃł��B
���剳[6]�́A�W���������ɇ@�ƈقȂ��Ă��܂����A���ڂƗގ��̉��@�藝�����藧���ŁA�o�Ȑ����ƌĂ����̒��� �����グ�Ă��܂��B
�����グ�Ă��܂��B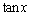 �̏ꍇ�͒�`�ł��Ȃ��Ƃ��낪����̂Ŗ��ɂ��Â炢�̂ł����A
�̏ꍇ�͒�`�ł��Ȃ��Ƃ��낪����̂Ŗ��ɂ��Â炢�̂ł����A �Ȃ炷�ׂĂ̎����Œ�`�ł���̂ŁA�������Ƃ��Ď��グ�₷���Ƃ����킯�ł��B
�Ȃ炷�ׂĂ̎����Œ�`�ł���̂ŁA�������Ƃ��Ď��グ�₷���Ƃ����킯�ł��B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���嗝�n���wTOP�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B